从Leafy Tree到WBLT
fush
·
·
算法·理论
更好的阅读体验。
UPD:2024/12/04 添加序列操作
UPD:2024/12/10 添加可持久化
前言
前面说过 FHQ-treap 的缺点在于常数。
这次篇文章要讲解 WBLT,码量与 FHQ-treap 差的不多,结构与线段树类似。
也可以分裂合并(不推荐),可持久化,但常数远小于 FHQ-treap。
美中不足的是:需要两倍的空间。 其实影响不大,
Leafy Tree
Leafy Tree 其实是一类树,它的核心思想在于将数据全部存放在叶节点中。
而我们耳熟能详的线段树本质上也属于 Leafy Tree。
Leafy Tree 实现二叉搜索树
注意,这一段的代码可以卡到单次 O(n) 的。
思路
我们可以先梳理 Leafy Tree 和 BST 的性质:
BST:
$~~~~$ 2. 插入一个值时,若 $val \le val_{rt}$,则向左走,否则向右走。
Leafy Tree:
$~~~~$ 1. 只有叶子结点维护的是原始信息。
$~~~~$ 2. 要么是叶子节点,要么有两个儿子。
我们显然无法同时满足四条性质。
但我们可以从第一条性质得到:$val_{ls} \le val_{rs}$。
那么我们可以维护区间最大值,并在插入的时候实现 $val_{ls} \le val_{rs}$ 即可。
那么雏形就出来了:
$~~~~$ 1. 非叶子节点维护的都是其所代表的区间的最大值。
$~~~~$ 2. $val_{ls} \le val_{rs}$。
$~~~~$ 3. 数据都处于叶子节点中。
### 查找
其实根据上面的内容,查找的方法已经呼吁而出:
$~~~~$ 如果当前节点是叶子节点,则若相等,则返回查找值,否则说明没有查找值。
$~~~~$ 如果 $val \le val_{ls}$,则去左儿子中找,否则去右儿子找。
```c++
bool find(int now, int x){
if(ifleaf(now))
return d[now].val == x;
if(x <= d[d[now].ls].val) return find(d[now].ls, x);
return find(d[now].rs, x);
}
```
### 插入
若当前是叶子节点:
$~~~~$ 新建两个节点,分别是当前节点的值,和插入节点的值。
$~~~~$ 把值较小的放在当前节点的左儿子,值较大的放在右儿子,然后跟新节点
否则,若 $val \le val_{ls}$,则进入左儿子,否则进入右儿子。
```c++
void insert(int val, int now){
if(ifleaf(now)){
int s1 = newnode(d[now].val), s2 = newnode(val);
if(d[now].val > val)swap(s1, s2);
d[now].ls = s1, d[now].rs = s2;
}
else (d[d[now].ls].val >= val) ? (insert(val, d[now].ls)) : (insert(val, d[now].rs));
pushup(now);
}
```
### 删除
若当前是叶子节点,直接退出。
若 $val \le val_{ls}$:
$~~~~$ 若左儿子是叶子节点且 $val == val_{ls}$ 将右儿子赋值为当前节点。
$~~~~$ 否则进入左儿子。
否则,对右儿子做相似的操作。
这样可以避免记录父亲节点。
```c++
void del(int &now, int x) {
if (d[d[now].ls].val >= x) {
if(ifleaf(d[now].ls))(d[d[now].ls].val == x) && (now = d[now].rs);
else del(d[now].ls, x), pushup(now);
}
else {
if(ifleaf(d[now].rs))(d[d[now].ls].val == x) && (now = d[now].ls);
else del(d[now].rs, x), pushup(now);
}
}
```
### 查询排名
若当前节点是叶子节点返回 $ans + 1$。
若 $val_{ls} \ge val$ 则进入左儿子。
否则,$ans \gets ans + size_{ls}$,然后进入右儿子。
```c++
int queryrank(int x){
int now = root, ans = 0;
while(1){
if(ifleaf(now))return ans + 1;
else if(d[d[now].ls].val >= x) now = d[now].ls;
else ans += d[d[now].ls].size, now = d[now].rs;
}
}
```
### 查询第 k 小
若当前节点是叶子节点:
$~~~~$ 若 $k = 1$,返回当前节点的权值。
$~~~~$ 否则返回特值
否则若 $val_{ls} \ge val$, 则进入左儿子。
否则,$k \gets k - size_{ls}$,然后进入右儿子。
```c++
int queryval(int k){
int now = root;
while(1){
if(d[now].size)return k == 1 ? d[now].val : -1;
else if(d[d[now].ls].size >= k) now = d[now].ls;
else k -= d[d[now].ls].size, now = d[now].rs;
}
}
```
### 前驱
第一种:
先找到 $k$ 的排名 $p$,输出第 $p-1$ 小。
```c++
int ask_pre(int k){return queryval(queryrank(k) - 1);}
```
第二种:
若当前节点是叶子节点,如果 $< k$ 更新答案,返回答案。
否则,如果 $val_{ls} \ge k$,进入左儿子找答案。
否则,用左儿子更新答案,进入右儿子。
```c++
int ask_pre(int val){
int ans = -1e9, now = root;
while(now){
if(ifleaf(now))return (d[now].val >= val ? ans : d[now].val);
else if(d[d[now].ls].val >= val)now = d[now].ls;
else ans = d[d[now].ls].val, now = d[now].rs;
}
}
```
### 后继
和前驱相差不大。
```c++
//第一种
int ask_next(int k){return queryval(queryrank(k + 1));}
//第二种
int ask_next(int val){
int ans = 0, now = root;
while(now){
if(ifleaf(now))return (d[now].val <= val ? ans : d[now].val);
else if(d[d[now].ls].val <= val)now = d[now].rs;
else ans = d[d[now].rs].val, now = d[now].ls;
}
return ans;
}
```
## WBLT
我们引入 Weight Balanced Tree(加权平衡树,又名 BB[$\alpha$]树)。
他的主要思想就是若左右子树比例不满足平衡系数 $\alpha$ 的话,则维护平衡。
若维护方式是重构的话,就是有名的替罪羊树。
若一棵子树 $T$ 的所有非叶子节点均满足 $\alpha$ 加权平衡,则认为这棵子树是 $\alpha$ 加权平衡的。
一棵 $\alpha$ 加权平衡的子树 $T$,其树高必然满足 $h \le \log n$。
证明:
$~~~~$ 从一个叶子节点向根节点走,每走一步维护的范围至少扩大到原来的 $\dfrac{1}{1 - \alpha}$。
$~~~~$ 树高就是 $O(\log_{\frac{1}{1 - \alpha}} n) = O(\log n)$。
当我们用 Leafy Tree 实现的 WBT 就是 WBLT。
WBT 满足 $h \le \log n$,所以 WBLT 除了合并的大部分操作都是 $O(\log n)$ 的。
其中 WBLT 的维护方式是旋转。
分为单旋和双旋。
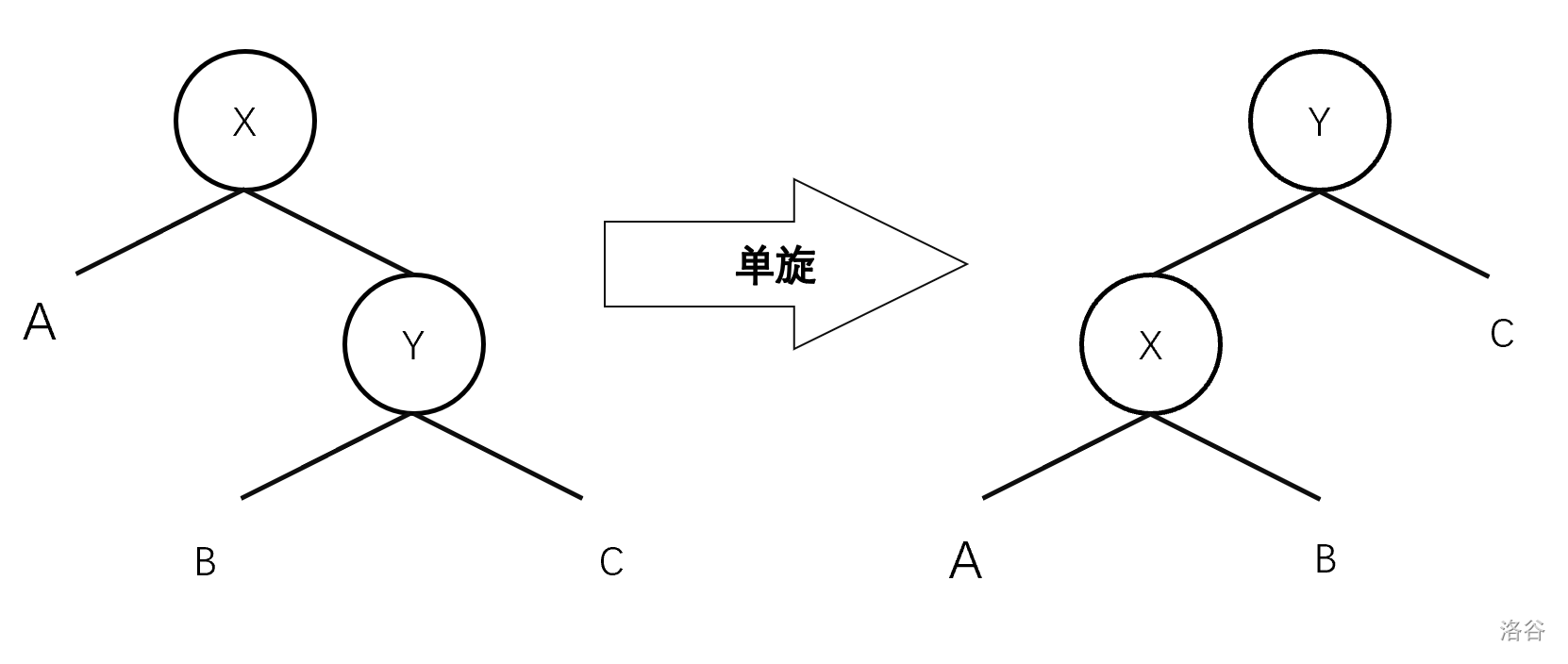
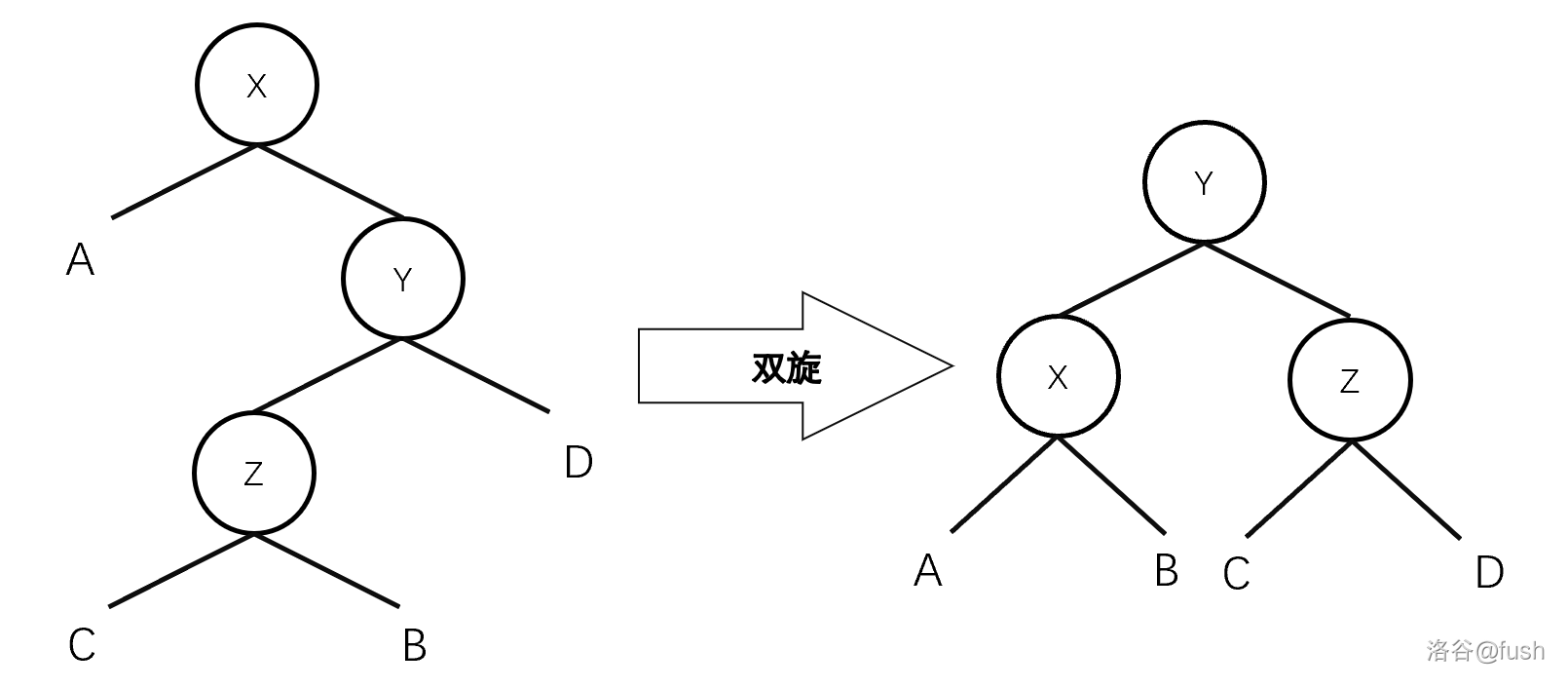
单次旋转的代码和其他平衡树差不多:
```c++
void rotate(int x, int dir) {
swap(d[x].ls, d[x].rs);
swap(d[d[x].ch[!dir]].ls, d[d[x].ch[!dir]].rs);
swap(d[d[x].ch[!dir]].ch[!dir], d[x].ch[dir]);
pushup(d[x].ls), pushup(d[x].rs), pushup(x);
}
```
平衡操作 OK 了,那么什么时候需要平衡呢?
首先,我们设节点的平衡度为 $\rho$, $\rho$ 的定义如下:
$$
\rho_{rt} = \dfrac{size_{son}}{size_{rt}}
$$
我们认为一个节点是平衡的,当且仅当 $\rho \ge \alpha, 1 - \rho \ge \alpha$。
若当前节点不平衡,若 $\rho_{son} \ge \dfrac{1 - 2\alpha}{1-\alpha}$,则进行双选,否则进行单旋。
为什么呢?我们来尝试证明一下:
以下证明来自 [博客larry76](https://www.cnblogs.com/larry76/p/17127392.html)。
我们根据单旋的图示,设 $\rho_x$ 为节点 $X$ 的平衡度,$\rho_y$ 表示节点 $Y$ 的平衡度,$\gamma_y$ 为单旋后节点 $Y$ 的平衡度。
根据图示和已知条件,我们可以得出:
$$
0 < \rho_x < \alpha\\
\alpha \le \rho_y \le 1 - \alpha
$$
根据图示和单旋的定义,我们不难看出 $\rho_x$、$\rho_y$、$\gamma_y$ 具有以下关系:
$$
\gamma = \rho_x + \rho_y - \rho_x \rho_y
$$
我们已知 $\rho_x$ 和 $\gamma_y$ 就是当前子树旋转前和旋转后的平衡度,而我们旋转后子树想要达到平衡,则需要:
$$
\alpha \le \gamma_y \le 1 - \alpha
$$
我们此时可以将目标拆成两部分,分别是:
$$
\begin{cases}
\gamma_y \ge \alpha\\
\gamma_y \le 1 - \alpha
\end{cases}
$$
此时,将 $\rho_x$、$\rho_y$、$\gamma_y$ 的关系代入不等式组,易得:
$$
\begin{cases}
\rho_x + \rho_y - \rho_x\rho_y \ge \alpha\\
\rho_x + \rho_y - \rho_x\rho_y \le 1 - \alpha
\end{cases}
$$
将式子稍微变形,即得:
$$
\begin{cases}
\rho_y \ge \frac{\alpha - \rho_x}{1 - \rho_x}\\
\rho_y \le \frac{1-\alpha-\rho_x}{1-\rho}
\end{cases}
$$
此时,我们可以得出下列两个命题:
$$
1.\rho_y \ge \frac{\alpha - \rho_x}{1-\rho_x}\\
2.\rho_y \le \frac{1-\alpha-\rho_x}{1-\rho_x}
$$
我们此时的问题也变成了证明上述两个命题在什么情况下同时成立。
命题 $1$ 在已知条件下是显然成立的,因为原命题等于:
$$
\rho_y \ge (\dfrac{\alpha-\rho_x}{1-\rho_x})_{\max}
$$
根据糖水不等式,易得:
$$
(\dfrac{\alpha - \rho_x}{1 - \rho})_{\max} = \alpha
$$
故此时,命题 $1$ 显然成立。
那么,关于命题 $2$,我们也可以有相似的证明过程:
$$
\rho_y \le (\dfrac{1-\alpha - \rho_x}{1-\rho_x})_{\min}
$$
根据糖水不等式,易得:
$$
(\dfrac{1-\alpha - \rho_x}{1-\rho_x})_{\min} = \dfrac{1-\alpha-\alpha}{1-\alpha} = \dfrac{1-2\alpha}{1-\alpha}
$$
代入原式,则得到:
$$
\rho_y \le \dfrac{1-2\alpha}{1-\alpha}
$$
此时我们可以看出,当 $\rho_y \in (\dfrac{1-2\alpha}{1-\alpha}, 1-\alpha]$ 的时候,命题二不成立,故我们需要对 $\rho_y$ 的范围进行收缩到 $\rho_y \in [\alpha, \dfrac{1-2\alpha}{1-\alpha}]$ 上述两个命题才同时成立。
综上,若单旋能维持平衡性,则需要 $\rho_y \le \dfrac{1-2\alpha}{1-\alpha}$,否则则必须进行双旋。
证毕。
所以维护是应当这么写:
若当前节点**左儿子的大小**与**当前节点的大小**的比值小于 $\alpha$,则:
$~~~~$ 若当前**右儿子的左儿子的大小**与当前**右儿子的大小**的比值大于等于 $\dfrac{1-2\alpha}{1-\alpha}$,则进行双旋。
$~~~~$ 否则进行单旋。
否则若当前节点**右儿子的大小**与**当前节点的大小**的比值小于 $\alpha$,则:
$~~~~$ 若当前**左儿子的右儿子的大小**与当前**左儿子的大小**的比值大于等于 $\dfrac{1-2\alpha}{1-\alpha}$,则进行双旋。
$~~~~$ 否则进行单旋。
```c++
void maintain(int now){
if(ifleaf(now))return;
int k;
if(d[d[now].ls].size < d[now].size * alpha)k = 1;
else if(d[d[now].rs].size < d[now].size * alpha)k = 0;
else return;
if(d[d[d[now].ch[k]].ch[!k]].size * (1 - alpha) >= d[d[now].ch[k]].size * (1 - 2 * alpha))
rotate(d[now].ch[k], !k);
rotate(now, k);
}
```
关于平衡因子 $\alpha$ 的取值问题,实际上只要取在区间 $[0,\dfrac{1}{2}]$ 之间的话都可以。
$\alpha = 0.29$ 即可 ,不过具体而言则是因题而异。
[完整代码(洛谷P3369)](https://www.luogu.com.cn/paste/gkiowhy8)。
## 区间操作
WBLT 可以像线段树一样打标记进行区间操作。
但是,遇到线段树不能维护的操作 WBLT 就没有办法了吗?
当然不是,WBLT 也可以分裂合并,其他的操作,我们可以像 FHQ-treap 一样将区间分裂出来进行维护。
将原本的树分裂成 $[1, l - 1]$,$[l, r]$,$[r + 1, n]$ 三个区间。
而中间的区间就是我们需要操作的,可以是情况操作。
操作完后再合并回去即可。
不过 WBLT 的分裂合并常数较大,也不好写,而且会有多余节点,需要做好垃圾节点的回收。
### 合并
设我们需要合并两棵 WBLT $L$ 和 $R$。
若 $\min(size_L, size_R) \ge \alpha \cdot (size_L+size_R)$,新建一个节点,左儿子是 $L$,右儿子是 $R$。
否则我们假设 $size_L \ge size_R
$~~~~$ 否则,**将 $L$ 的左子树与 $L$ 的右子树的左子树合并结果作为最终左子树,将 $L$ 的右子树的右子树与 $R$ 合并后的结果作为最终右子树**。
反之亦然。
时间复杂度:$O(\log \dfrac{\max(size_L, size_R)}{\min(size_L, size_R)})$。
```c++
int merge(int x, int y) {
if (!x || !y) return x | y;
int t = d[x].size + d[y].size;
if (min(d[x].size, d[y].size) >= alpha * t)
return d[t = newnode(0)].ls = x, d[t].rs = y, pushup(t), t;
if (d[x].size >= d[y].size) {
pushdown(x);
if (d[d[x].ls].size >= alpha * t)
return d[x].rs = merge(d[x].rs, y), pushup(x), x;
pushdown(d[x].rs);
d[x].ls = merge(d[x].ls, d[d[x].rs].ls), delnode(d[x].rs);
return d[x].rs = merge(d[d[x].rs].rs, y), pushup(x), x;
}
pushdown(y);
if (d[d[y].rs].size >= alpha * t)
return d[y].ls = merge(x, d[y].ls), pushup(y), y;
pushdown(d[y].ls);
d[y].rs = merge(d[d[y].ls].rs, d[y].rs), delnode(d[y].ls);
return d[y].ls = merge(x, d[d[y].ls].ls), pushup(y), y;
}
```
合并的讲解已经结束,赶时间的可以跳过这一段。
网上有一种写法:
```c++
int merge(int x, int y) {
if (!x || !y) return x | y;
int t = newnode(0);
lp[t] = x, rp[t] = y;
pushup(t), maintain(t);
return t;
}
```
看起来挺有道理的。但我们考虑这种情况:
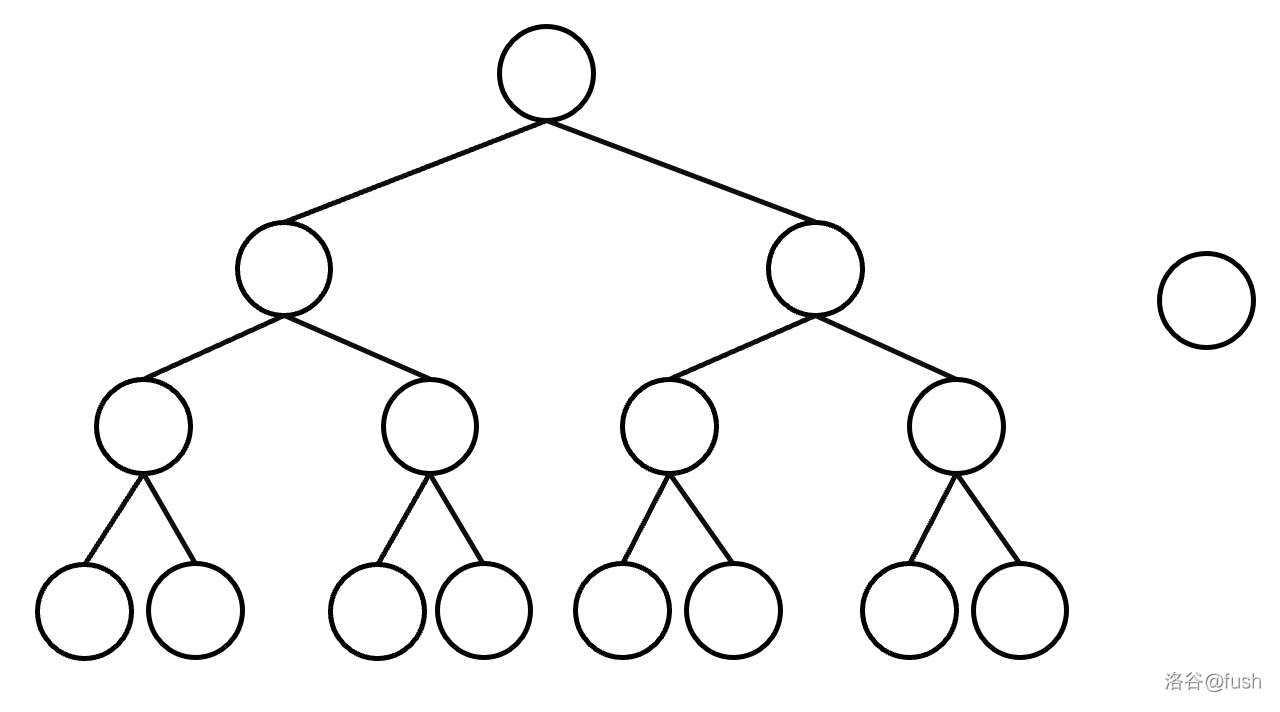
即一棵是满二叉树,一棵只有一个节点,这时合并会变成:
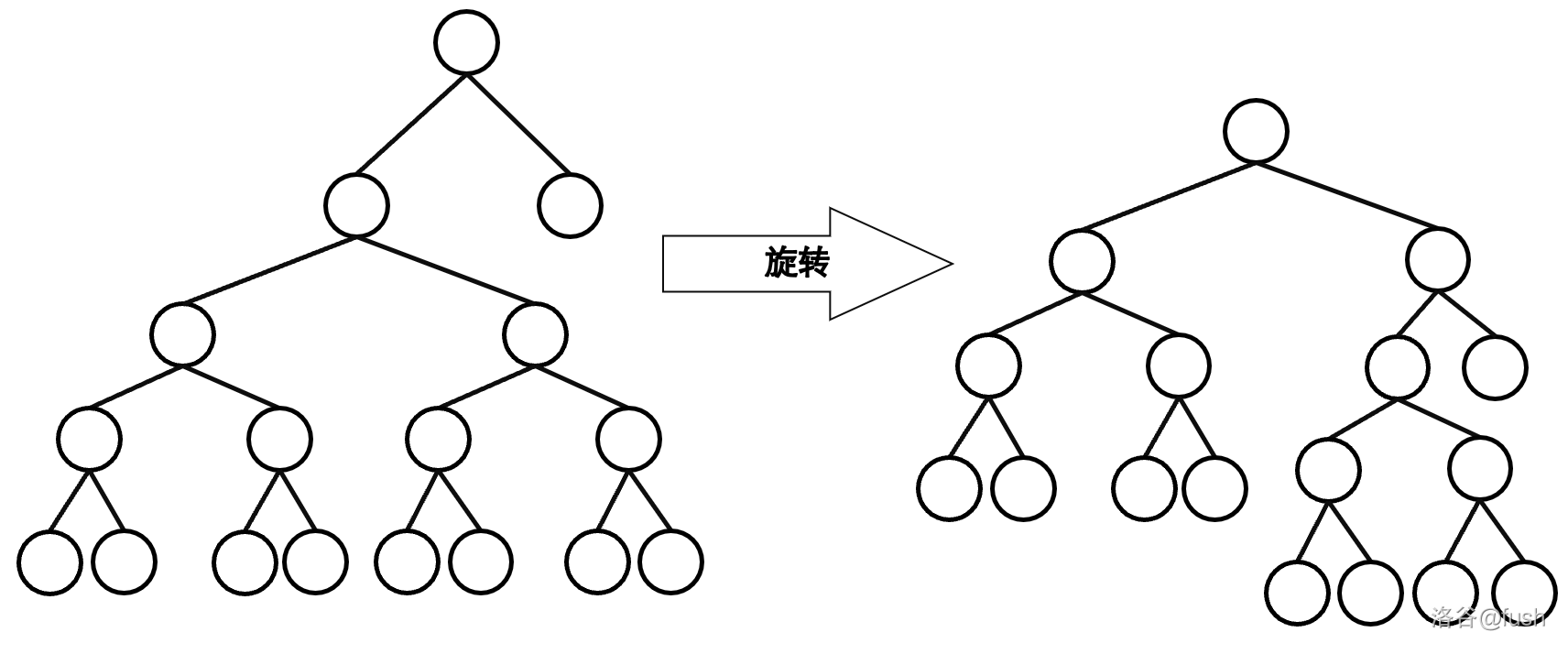
这样明显不满足 $\alpha$ 加权平衡(~~但是基本没人卡~~)。
### 分裂
跟 FHQ-treap 差不多。
但要用 `merge` 保持满足 $\alpha$ 加权平衡。
分裂的复杂度:$O(\log n)$。
#### 按权值分裂
若到达叶子节点,若权值 $\le k$ 分到 $x$,否则分到 $y$。
否则,若 $val_{ls} \le k$,那么将 $ls$ 分给 $x$,进入右儿子继续分。
否则,将 $rs$ 分给 $y$,进入左儿子继续分。
```c++
void split(int now, int k, int &x, int &y) {
if(ifleaf(now)){
if(d[now].val <= k)x = now, y = 0;
else x = 0, y = now;
return;
}
pushdown(now)
if(k >= d[d[now].ls].val){
split(d[now].rs, k, x, y);
delnode(now), x = merge(d[now].ls, x);
}
else{
split(d[now].ls, k, x, y);
delnode(now);
y = merge(y, d[now].rs);
}
}
```
#### 按排名分裂
与按权值分裂相差不大。
```c++
void split(int now, int k, int &x, int &y) {
if(k == 0)return x = 0, y = now, void();
if(ifleaf(now))
return void(k ? (x = now, y = 0) : (x = 0, y = now));
pushdown(now);
if(k >= d[d[now].ls].size){
split(d[now].rs, k - d[d[now].ls].size, x, y);
delnode(now), x = merge(d[now].ls, x);
}
else{
split(d[now].ls, k, x, y);
delnode(now), y = merge(y, d[now].rs);
}
}
```
[洛谷P3391文艺平衡树代码](https://www.luogu.com.cn/paste/21kiybds)
## 可持久化
不知道什么是可持久化的看这:[可持久化数据结构简介](https://fush-git.github.io/2024/12/10/可持久化数据结构是什么/)。
具体操作就是,每次传进去一个新的根(副本)。
然后在插入、删除、旋转时把需要更改的点全部新建一遍。
剩下的地方都是可以跟之前公用的。
其实也挺好写的,加些点就好了。
这里是代码中重要的,其他地方的区别就不放了。
```c++
void copynode(int &i){if(i)d[++tot] = d[i], i = tot;}//将节点复制
void maintain(int&now){//注意是引用
if(ifleaf(now))return;
int k;
if(d[d[now].ls].size < d[now].size * alpha)k = 1;
else if(d[d[now].rs].size < d[now].size * alpha)k = 0;
else return;
if(d[d[d[now].ch[k]].ch[!k]].size >= d[d[now].ch[k]].size * (1 - 2 * alpha) / (1 - alpha))rotate(d[now].ch[k], !k);
rotate(now, k);
}
void rotate(int&x, int dir) {//注意是引用
copynode(x), copynode(d[x].ch[!dir]);//add
swap(d[x].ls, d[x].rs);
swap(d[d[x].ch[!dir]].ls, d[d[x].ch[!dir]].rs);
swap(d[d[x].ch[!dir]].ch[!dir], d[x].ch[dir]);
pushup(d[x].ch[!dir]), pushup(x);
}
void insert(int val, int&now){//注意是引用
copynode(now);//add
if(ifleaf(now)){
int s1 = newnode(d[now].val), s2 = newnode(val);
if(d[now].val > val)swap(s1, s2);
d[now].ls = s1, d[now].rs = s2;
return pushup(now);
}
else (d[d[now].ls].val >= val) ? (insert(val, d[now].ls)) : (insert(val, d[now].rs));
return pushup(now), maintain(now);
}
void del(int x, int &now) {
copynode(now);//add
if (d[d[now].ls].val >= x) {
if(ifleaf(d[now].ls)){
if(d[d[now].ls].val != x)return;
now = d[now].rs, copynode(now);//add
}
else del(x, d[now].ls);
}
else {
if(ifleaf(d[now].rs)){
if(d[d[now].rs].val != x)return;
now = d[now].ls, copynode(now);//add
}
else del(x, d[now].rs);
}
return pushup(now), maintain(now);
}
```
其中有注释的是更改过的(下同)。
而一次操作最多涉及 $\log n$ 个点,所以空间是 $\log n$ 级别的。
[洛谷P3835可持久化平衡树代码](https://www.luogu.com.cn/paste/3ilx9qoc)