P4914 题解
Chinese_zjc_
·
·
题解
先看下面这张图:
从题目配图中显然可以看出, $ A $ , $ B $ , $ C $ , $ D $ , $ E $ 五点之间的相对位置不会改变.
那我们直接可以把 $ v $ , $ t $ 这些量忽略掉,于是这道题目就成了静态.
而且由于正五边形存在对称轴,因此只需要考虑 $ 3 $ 个点 $C$ , $ D $ , $E$ 能否攻击到 $ A $ .
我们设 $ A:(0,0) $ , $ B $ 在 $ y $ 轴上.
易得: $ B:(0,R) $ , $ C:(0,R-r) $ ,正五边形关于 $ y $ 轴对称.
然后我们来求 $ D $ 和 $ E $ 的坐标.
作 $ BF\bot BC$交于点 $ B $ , $ DF\bot BF $ 交于点 $ F $ , $EG\bot BF$交于点 $ G $ .
如图:
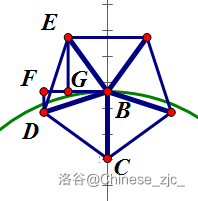
则易得 $ \angle DBF=18^\circ $ , $ \angle EBG=54^\circ $ .
再使用三角函数,即得: $ D:(-\cos(18^\circ)\times r,R-\sin(18^\circ)\times r) $ , $ E:(-\cos(54^\circ)\times r,R+\sin(54^\circ)\times r) $ .
再考虑子弹方向:
对于 $ D $ 和 $ E $ 第一个子弹的方向分别是射线 $ DF $ 和射线 $ GE $ .
对于第 $ i+1 $ 个子弹,相对于第 $ 1 $ 个子弹顺时针旋转了 $ \frac{360^\circ}{k}\times i $ .
因此若 $ D $ 或 $ E $ 要射到 $ A $ , $ 180^\circ-\angle AEG $ 或 $ 180^\circ-\angle AFD $ 必须得是 $ \frac{360^\circ}{k} $ 的倍数.
让我们求出 $ \angle AEG $ 和 $ \angle AFD $ 的度数.
依然是三角函数:
$$
\angle AEG=\arctan(\frac{\cos(18^\circ)\times r}{R-\sin(18^\circ)\times r})\\
\angle AFD=\arctan(\frac{\cos(54^\circ)\times r}{R+\sin(54^\circ)\times r})\\
$$
这样,直接计算判断即可,而 $ B $ 射到 $ A $ 的情况显然当且仅当 $ k $ 为偶数.
那我们就可以愉快地写代码了.
$Code\ \#1$:
```cpp
//This Code was made by Chinese_zjc_.
#include<cstdio>
#include<cmath>
#define int long long
#define PI 3.14159265358979323
#define EQUAL 0.00000000000001
#define double long double
using namespace std;
int T,k;
double r,R,v,t,siz[5],atime;
bool answered;
double _360topi(const double IN)
{
return IN/180*PI;
}
signed main()
{
scanf("%lld",&T);
while(T--)
{
scanf("%Lf%Lf%Lf%Lf%lld",&r,&R,&v,&t,&k);
answered=false;
if(!(k&1))
{
puts("no");
continue;
}
siz[1]=_360topi(180)-atan((cos(_360topi(18))*r)/(R-sin(_360topi(18))*r));
siz[2]=_360topi(180)-atan((cos(_360topi(54))*r)/(R+sin(_360topi(54))*r));
atime=PI*2/k;
for(int i=1;i<=2;++i)
{
int tim=siz[i]/atime+EQUAL;
if(abs(tim*atime-siz[i])<EQUAL)
{
puts("no");
answered=true;
break;
}
}
if(!answered)
{
puts("yes");
}
}
return 0;
}
```
回头看到式 $ (1) $ ,这就不禁让人想问了:
**是不是它们都是无理数?**
这是显然的,证明略.
那我们就可以拿出我们在二年级就学过的知识:
无理数除以一个有理数的结果必定为无理数.
很显然,因此证明略.
那代码可以进行简化:
$Code\ \#2$:
```cpp
//This Code was made by Chinese_zjc_.
#include<cstdio>
using namespace std;
int T,k;
double r,R,v,t;
signed main()
{
scanf("%lld",&T);
while(T--)
{
scanf("%lf%lf%lf%lf%lld",&r,&R,&v,&t,&k);
puts(k&1?"yes":"no");
}
return 0;
}
```