题解 CF19E 【Fairy】
command_block
·
·
题解
题意 : 给出一张无向图,求删除一条边后此图变成二分图的所有方案。
------------
本题数据范围较弱,但存在线性做法。
考虑二分图的充要条件 : 不存在奇环。
若原图本就为二分图,显然随意删除都可行。
否则,图中存在奇环,我们需要删一条边破坏图中所有的奇环。
显然,答案是**所有奇环的交集中的边**。
但是,奇环的个数可能非常多,不可能实际求解交集。
接下来的思路受到 [P4151 [WC2011]最大XOR和路径](https://www.luogu.com.cn/problem/P4151) 的启发。
一个自交的奇环必然引出一个简单奇环,所以我们只需要考虑**简单环**。
对于图中的一个连通块,先求出任意一个生成树,然后查看非树边。
此时容易处理只含有一条非树边的环,且每条非树边恰好对应一个这样的环,我们把这种环叫做**本原环**。
- **树边**
若某条非树边形成的本原环是奇环,则这条边是坏边,否则是好边。
对于一条非树边,称其本原环中的树边被其覆盖。
- **性质①** : 答案边 $\Rightarrow$ 被所有坏边覆盖
考虑每个坏边形成的奇环,显然。
- **性质②** : 答案边不会被好边覆盖
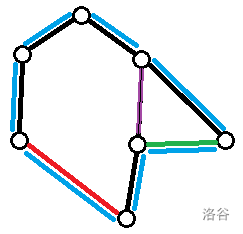
图中黑色为树边。
(反证)一条答案边(紫色)肯定被某条坏边(绿色)覆盖。
然而,该坏边和好边(红色)的本原环异或并一定能组成一个奇环(蓝色)。
原因 : 奇环 + 偶环 - 消去两次的公共部分 = 奇环
这个奇环一定不包含刚才提到的答案边,矛盾。
- **性质③** : 不被任何好边覆盖,且被所有坏边覆盖的边,就是答案边。
对于某个简单环,将其中所有非树边的本原环进行异或并,能得到它本身。
若非树边中有奇数个坏边,则形成奇环,否则是偶环。
对于一条不被任何好边覆盖的边,其在异或并中是否出现取决于坏边对其覆盖的次数。
若改变被所有坏边覆盖,则在此时恰好被覆盖奇数次,总是被包含在异或并中。
根据性质③,容易想到如下算法。
我们统计只含有一条非树边的奇环数量,设为 $cnt$。
对于坏边,则将其覆盖的边 $+1$ ,好边则将其覆盖的边 $-1$。
最后边权为 $cnt$ 的边即为答案。
朴素的链加处理方法——树上差分需要求 $\rm lca$ ,复杂度带 $\log$。
但是,注意到我们进行操作的是非树边,在 $\rm dfs$ 的过程中,所有非树边都是返祖边,所以容易 $O(1)$ 实现差分。
- **非树边**
若 $cnt=1$ ,则可以删除唯一的一条坏边,否则坏边不可删除。
------------
注意,本题没有 $\rm SPJ$ ,需要将边的编号排序。
```cpp
#include<algorithm>
#include<cstdio>
#include<vector>
#define pb push_back
#define MaxN 10500
using namespace std;
vector<int> g[MaxN],p[MaxN];
int cnt,s[MaxN],sp,ans[MaxN],tn;
bool dis[MaxN],vis[MaxN],e[MaxN];
void pfs(int u)
{
vis[u]=1;
for (int i=0,v;i<g[u].size();i++)
if (!vis[v=g[u][i]]){
dis[v]=dis[u]^1;
e[p[u][i]]=1;
pfs(v);
}else if (!e[p[u][i]]){
e[p[u][i]]=1;
if (dis[u]==dis[v]){
cnt++;s[u]++;s[v]--;
sp=p[u][i];
}else {s[u]--;s[v]++;}
}
}
void dfs(int u)
{
vis[u]=1;
for (int i=0,v;i<g[u].size();i++)
if (!vis[v=g[u][i]]){
dfs(v);
if (s[v]==cnt)ans[++tn]=p[u][i];
s[u]+=s[v];
}
}
int n,m;
int main()
{
scanf("%d%d",&n,&m);
for (int i=1,u,v;i<=m;i++){
scanf("%d%d",&u,&v);
g[u].pb(v);p[u].pb(i);
g[v].pb(u);p[v].pb(i);
}
for (int i=1;i<=n;i++)
if (!vis[i])pfs(i);
if (!cnt){
printf("%d\n",m);
for (int i=1;i<=m;i++)
printf("%d ",i);
return 0;
}
for (int i=1;i<=n;i++)vis[i]=0;
for (int i=1;i<=n;i++)
if (!vis[i])dfs(i);
if (cnt==1)ans[++tn]=sp;
printf("%d\n",tn);
sort(ans+1,ans+tn+1);
for (int i=1;i<=tn;i++)
printf("%d ",ans[i]);
return 0;
}
```