P8544 「Wdoi-2」禁断之门对面,是此世还是彼世
Arghariza
·
·
题解
https://www.cnblogs.com/Ender32k/p/17713788.html
Part 1. 转换
由于 A_{i,j}=a_ib_j,这个 f(B) 显然可以化简:
\begin{aligned}f(B)&=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^t\sum\limits_{k=\min(B_{i,j},B_{i+1,j})}^{\max(B_{i,j},B_{i+1,j})}A_{i,k}\\&=\sum\limits_{i=1}^n\sum\limits_{j=1}^t\sum\limits_{k=\min(B_{i,j},B_{i+1,j})}^{\max(B_{i,j},B_{i+1,j})}a_ib_k\\&=\sum\limits_{i=1}^na_i\sum\limits_{j=1}^tS_{\max(B_{i,j},B_{i+1,j})}-S_{\min(B_{i,j},B_{i+1,j})-1}\end{aligned}
发现若得到 $g(B_1,B_2)=\sum\limits_{j=1}^tS_{\max(B_{1,j},B_{2,j})}-S_{\min(B_{1,j},B_{2,j})-1}$ 的最小值,我们可以令 $B_{2k+1}=B_1,B_{2k+2}=B_2$。这样显然最优。也就是说,$f(B)=\left(\sum\limits_{i=1}^na_i\right)\cdot \min g(B_1,B_2)$。
问题转换为找到一个 $B_1,B_2$,分别满足每个元素两两不同,都在 $[1,m]$ 之间,并且对应的位置上的元素不同,使得 $g(B_1,B_2)$ 最小。
由于同一行元素两两不同以及值域的限制,考虑转换成匹配问题。相当于现在有两列数(分为左部和右部),分别为 $1,2,\cdots ,m$,在左部中选择 $t$ 个数,并和右部的 $t$ 个数匹配。满足不存在形如 $(i,i)$ 的匹配,一对匹配 $(i,j)$ 的价值就是 $S_{\max(i,j)}-S_{\min(i,j)-1}$,也就是 $b_{\min(i,j)}+b_{\min(i,j)+1}+\cdots+b_{\max(i,j)}$。一组匹配的价值就是每对匹配的价值之和,求**钦定有 $t$ 对匹配的最小匹配**。
#### Part 2. 猜想
有个比较感性的想法,就是**一对匹配不应该跨过太大的距离**。考虑从左到右按顺序匹配,如果匹配跨过了一段空区间,那么不如不跨过这段区间,因为这样减小了代价的同时也给后面的点更多的选择方案。
另一个比较感性的想法,**匹配应该尽可能不交叉**。这里借用[这篇题解](https://www.luogu.com.cn/blog/McHf/solution-Wdoi2-1E)的图:
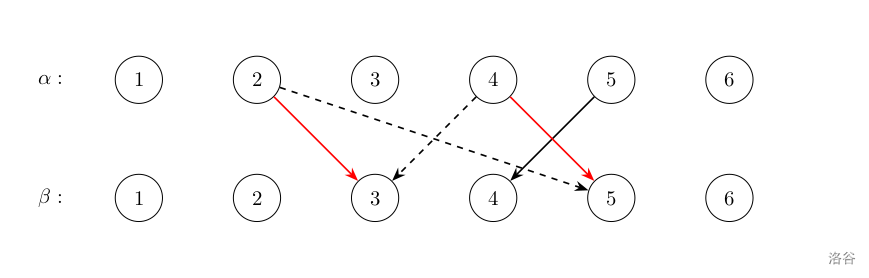
如上图,匹配 $(2,5)(4,3)$ 显然不如匹配 $(2,3),(4,5)$。即如果存在交叉的匹配,我们尝试交换匹配以减少价值。而且可以发现减少交叉必定不劣。
手玩一些数据之后,我们发现最优解中,$i$ 只能形成 $(i,j)(j\in \{i-2,i-1,i+1,i+2\})$ 的匹配。我们下面试图证明这个结论。
#### Part 3. 证明
$i$ 显然可以和 $i-1,i+1$ 匹配,即证最优解中合法匹配 $(i,j)$ 满足 $j-i\le 2$。下面**从左到右**考虑一组匹配 $(i,j)(j>i+2)$ 如何调整(小于 $i$ 的左部点的匹配均满足猜想),$j<i-2$ 根据对称性同理:
- 若 $\exists k\in \{1,2\}$,不存在匹配 $(?,i+k)$(即右部的 $i+k$ 没有被匹配),显然将 $(i,j)$ 调整为 $(i,i+k)$ 更优。
- 否则存在 $(x,i+1),(y,i+2)$ 的匹配,且我们从左到右调整,显然有 $x,y>i$ 且 $x\neq y$。注意到匹配 $(i,j)$ 和 $(x,i+1),(y,i+2)$ 都有上述的**交叉**,所以我们试图交换两个匹配的右部点以减少交叉:若 $x=j$,则 $y\neq j$,将原匹配 $(i,j)(y,i+2)$ 重组为 $(i,i+2)(y,j)$ 即可;若 $x\neq j$,将原匹配 $(i,j)(x,i+1)$ 重组为 $(i,i+1)(x,j)$ 即可。
这样我们就能够将任意的合法匹配调整为更优的、满足 $i$ 只能形成 $(i,j)(j\in \{i-2,i-1,i+1,i+2\})$ 的匹配的方案。
最终只剩下三种结构:连续的三元环,例如 $(i,i+1)(i+1,i+2)(i+2,i)$ ;连续的二元环,例如 $(i,i+1)(i+1,i)$;连续的一条链,例如 $(i,i+1)(i+1,i+2)(i+2,i+3)\cdots (i+k,i+k+1)$。前两种情况有交叉,但是无法调整;并且能够发现,只有前两种情况无法调整。
#### Part 4. 你会了
然后就能考虑 dp 了:令 $f_{i,j,0/1}$ 表示目前考虑到 $i$ 的匹配 $(i,?)$,前 $i$ 个点一共有 $j$ 对匹配,目前是否在一条形如 $(u,u+1)(u+1,u+2)\cdots(i-1,i)$ 的链中。
- $f_{i,j,1}\gets f_{i-1,j-1,1}+b_{i}+b_{i-1}$,表示延续一条链,增加一对匹配,连接 $(i-1,i)$。
- $f_{i,j,1}\gets f_{i-2,j-1,0}+b_i+b_{i-1}$,表示新建一条链,增加一对匹配,连接 $(i-1,i)$。
- $f_{i,j,0}\gets f_{i-2,j-2,0}+2(b_i+b_{i-1})$,表示新增一个二元环,增加两对匹配,连接 $(i-1,i)(i,i-1)$。
- $f_{i,j,0}\gets f_{i-3,j-3,0}+2b_i+3b_{i-1}+2b_{i-2}$,表示新增一个三元环,增加三对匹配,连接 $(i-2,i-1)(i-1,i)(i,i-2)$ 或者 $(i,i-1)(i-1,i-2),(i-2,i)$。
- $f_{i,j,0}\gets f_{i-1,j,0}$,表示 $i$ 没有匹配任何点。
- $f_{i,j,0}\gets f_{i,j,1}$,表示我摆烂了,不延续一条链。
乍一看是 $O(mt)$ 的?的确是 $O(mt)$ 的。
考虑瓶颈在于强制选择 $t$ 对匹配,对于这类问题,我们可以通过证明答案随匹配数的变化具有凸性,而进行 wqs 二分。
这题的凸性十分显然,因为是匹配问题,可以转化成费用流模型:
- 有超源 $S'$ 和超汇 $T'$,源点 $S$ 和汇点 $T$,$S'\to S$ 连流量 $t$,费用 $0$ 的边(以下 $u\to v$ 连流量 $f$ 费用 $w$ 的边简记为 $u\to v(f,w)$)。即 $S'\to S(t,0),T\to T'(t,0)$。
- 记 $i$ 的左部点为 $l_i$,右部点为 $r_i$,$S\to l_i(1,0),r_i\to T(1,0)$。
- 对于 $i\neq j$,$l_i\to r_i(1,S_{\max(i,j)}-S_{\min(i,j)-1})$。
不难发现最小费用最大流就是答案。根据费用流函数的凸性,原问题具有凸性,可以 wqs 二分。具体地,二分斜率 $k$,新建一对匹配时,直接减去 $k$ 的代价即可。
最终复杂度 $O(n\log V)$。代码好写得很。
```cpp
// Problem: P8544 「Wdoi-2」禁断之门对面,是此世还是彼世
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8544
// Memory Limit: 512 MB
// Time Limit: 2500 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace vbzIO {
char ibuf[(1 << 20) + 1], *iS, *iT;
#if ONLINE_JUDGE
#define gh() (iS == iT ? iT = (iS = ibuf) + fread(ibuf, 1, (1 << 20) + 1, stdin), (iS == iT ? EOF : *iS++) : *iS++)
#else
#define gh() getchar()
#endif
#define mt make_tuple
#define mp make_pair
#define fi first
#define se second
#define pc putchar
#define pb emplace_back
#define ins insert
#define era erase
typedef tuple<int, int, int> tu3;
typedef pair<int, int> pi;
inline int rd() {
char ch = gh();
int x = 0;
bool t = 0;
while (ch < '0' || ch > '9') t |= ch == '-', ch = gh();
while (ch >= '0' && ch <= '9') x = (x << 1) + (x << 3) + (ch ^ 48), ch = gh();
return t ? ~(x - 1) : x;
}
inline void wr(int x) {
if (x < 0) x = ~(x - 1), putchar('-');
if (x > 9) wr(x / 10);
putchar(x % 10 + '0');
}
}
using namespace vbzIO;
const int N = 5e5 + 100;
const int P = 1e9 + 7;
const int inf = 1e12;
int n, m, t, sum, b[N];
pi f[N][2];
pi operator + (const pi &lh, const pi &rh) {
return mp(lh.fi + rh.fi, lh.se + rh.se);
}
pi chk(int w) {
for (int i = 0; i <= m; i++)
f[i][0] = f[i][1] = mp(inf, 0);
f[0][0] = mp(0, 0);
for (int i = 1; i <= m; i++) {
f[i][1] = min(f[i][1], f[i - 1][1] + mp(b[i] + b[i - 1] - w, 1));
if (i >= 2) f[i][1] = min(f[i][1], f[i - 2][0] + mp(b[i] + b[i - 1] - w, 1));
if (i >= 2) f[i][0] = min(f[i][0], f[i - 2][0] + mp(2 * (b[i] + b[i - 1] - w), 2));
if (i >= 3) f[i][0] = min(f[i][0], f[i - 3][0] + mp(2 * b[i] + 2 * b[i - 2] + 3 * b[i - 1] - 3 * w, 3));
f[i][0] = min(min(f[i][0], f[i - 1][0]), f[i][1]);
}
return f[m][0];
}
signed main() {
n = rd(), m = rd(), t = rd();
for (int i = 1; i <= n; i++)
(sum += rd()) %= P;
for (int i = 1; i <= m; i++) b[i] = rd();
int l = 0, r = 3e9, res = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (chk(mid).se <= t) res = mid, l = mid + 1;
else r = mid - 1;
}
wr(((chk(res).fi % P + res * t % P) % P + P) * sum % P);
return 0;
}
```