分拆数与 q-analog 小记
WorldMachine
·
2025-09-19 18:07:22
·
算法·理论
感觉大脑严重退化了!
一.分拆数
§1.1 基本定义
首先考虑一个较平凡的东西:有序分拆 ,也就是将 n 表示成若干个正整数 a_1,\dots,a_k 的和,元素之间有序,很容易发现这等价于在 n-1 个空位中插 k-1 个隔板,如果限制个数那方案数就是 \dbinom{n-1}{k-1} ,不限制就是 2^{n-1} 。
如果只要求是非负整数,可以把每个 a_i 都加上 1 ,这样就变成把 n+k 分成 k 个有序部分的方案,方案数即为 \dbinom{n+k-1}{k-1}=\dbinom{n+k-1}{n} 。如果只限制 k\le m ,总方案数就是 \sum\limits_{k=1}^m\dbinom{n+k-1}{n}=\dbinom{n+m}{n+1} 。
下面说的主要都是无序分拆 。
定义 1.1.1
将 n 表示成若干个不递增正整数 a_1,\dots,a_k 的和的方案称为 n 的分拆 ,称 a_i 为该分拆的一个部分 。
考虑如何递推地求出 p(n,k) 。将全体 a_i 减去 1 并去掉为 0 的部分,会得到将 n-k 分拆成不超过 k 个部分的方案,因此有:
\begin{aligned}
p(n,k)&=\sum_{i=0}^kp(n-k,i)\\
p(n,k)-p(n-1,k-1)&=\sum_{i=0}^kp(n-k,i)-\sum_{i=0}^{k-1}p(n-k,i)\\
p(n,k)&=p(n-1,k-1)+p(n-k,k)
\end{aligned}
定理 1.1.2
分拆数 p(n) 的 OGF 为:
\widetilde{p}(x)=\sum_{n=0}^{\infty}p(n)x^n=\prod_{i=1}^{\infty}\dfrac{1}{1-x^i}
证明:对每个 m\in\mathbb Z_+ 决策选 m 的个数,由 \sum\limits_{i=0}^{+\infty}x^{ni}=\dfrac{1}{1-x^n} 立得。
对于 k -分拆数,也有类似的结论:
定理 1.1.3
$$
\widetilde{p}(x,y)=\sum_{n=0}^{\infty}\sum_{k=0}^{n}p(n,k)x^ny^k=\prod_{i=1}^\infty\dfrac{1}{1-x^iy}
$$
证明和上面是类似的。
定理 1.1.4
将 n 分拆成若干互不相同正整数的方案数(即互异分拆数 ,记作 p_d(n) )等于将 n 分拆成若干正奇数的方案数(即奇分拆数 ,记作 p_o(n) )。
证明:易知 p_d(n) 的 OGF 为 \widetilde{p_d}(x)=\prod\limits_{i=1}^\infty(1+x^i) ,p_o(n) 的 OGF 为 \widetilde{p_o}(x)=\prod\limits_{i=1}^\infty\dfrac{1}{1-x^{2i-1}} 。
用平方差将第一个级数变形:
\prod\limits_{i=1}^\infty(1+x^i)=\prod_{i=1}^\infty\dfrac{1-x^{2i}}{1-x^i}
对于 1-x^i ,若 i 为奇数,其次数为 -1 ,否则 i 和 \dfrac i2 处贡献相抵,故有 \prod\limits_{i=1}^\infty(1+x^i)=\prod\limits_{i=1}^\infty\dfrac{1}{1-x^{2i-1}} ,即 p_d(n)=p_o(n) 。
该定理还有一个简单的组合证明:将互异分拆 a_1+\dots+a_m 拆为 2^{k_1}b_1+\dots+2^{k_m}b_m ,其中 b_1,\dots,b_m 均为奇数,该过程可逆,因此是双射。
§1.2 Ferrers 图
定义 1.2.1
将 n 的一个分拆 a_1,\dots,a_k 用点阵表示,共 k 行,第 i 行有 a_i 个点,称其为该分拆的 Ferrers 图 。如果把点换成一个个的小正方形,此时的图又称之为 Young 图。
贺一张《组合数学》上的图,下面是 12=5+4+2+1 对应的 Ferrers 图:
将其行列翻转会得到新的 Ferrers 图,她对应的分拆称为原分拆的共轭 ,例如 5+4+2+1 的共轭即为 4+3+2+2+1 ,实际上也可看做为 b_i=\sum\limits_{j=1}^k[a_j\ge i] 。
由此可得:
定理 1.2.2
满足 a_1\le k 的分拆方案数为 p(n,k) 。
下考虑一类特殊的分拆,其共轭和原分拆相同,称其为自共轭分拆 ,其对应的 Ferrers 图称为自共轭 Ferrers 图 。
例如 21=7+5+3+2+2+1+1 对应的 Ferrers 图:
定理 1.2.3
自共轭分拆的个数等于互异奇分拆数 ,其 OGF 为 \widetilde{p_{od}}(x)=\prod\limits_{i=1}^{\infty}(1+x^{2i-1}) 。
证明:考虑构造双射,对于自共轭分拆 a ,找到自共轭 Ferrers 图中以左上角为顶点的最大正方形,设其边长为 r ,可以构造一个项数为 r 的互异奇分拆 b ,满足 b_i=2a_i-2i+1 :
故结论成立。
称该正方形的边长 r 为该自共轭分拆的阶 ,记 p_{od}(n,r) 为 n 的 r 阶自共轭分拆数,也即将 n 拆分为 r 个互异正奇数的方案数,其 OGF 为 \widetilde{p_{od}}(x,y)=\sum\limits_{n=0}^{\infty}\sum\limits_{r=0}^{\infty}p_{od}(n,r)x^ny^{r} ,易知有:
\widetilde{p_{od}}(x,y)=\prod_{i=1}^{\infty}(1+x^{2i-1}y)
下证明一个双射,并由此证明 Jacobi 三重积恒等式:
定理 1.2.4
对于任意非负整数 l ,n 的任一分拆都和一对和为 2n+l^2 、阶之差为 l 的自共轭分拆一一对应。
证明:画出 Ferrers 图,找到经过从上往下第 l+1 个点的自左上至右下的对角线,它将原图分为两部分:
将这两部分按该对角线对称,并给黄色部分加上 l\times l 的正方形,这样会得到两个自共轭 Ferrers 图,其点数和为 2n+l^2 ,阶之差为 l :
如果对角线在整个图下面,那红色部分就空了,黄色部分就是把原图整个对称然后拼上一个 l\times l 的正方形。
也容易得到由一对合法的自共轭 Ferrers 图得到一个分拆的方法,因此这是一个双射。
写成柿子就是:
p(n)=\sum_{r=0}^{\infty}\sum_{i=0}^{2n+l^2}p_{od}(i,r)p_{od}(2n+l^2-i,l+r)
下面给出 Jacobi 三重积恒等式的一个证明,这个定理还能和模形式等巴拉巴拉的东西扯上关系。
定理 1.2.5(Jacobi 三重积恒等式)
\prod_{n=1}^{\infty}(1-q^{2n})(1+zq^{2n-1})(1+z^{-1}q^{2n-1})=\sum_{n\in\mathbb Z}z^nq^{n^2}
证明:先令 x^2=z ,先把 1-q^{2n} 除过去,右边等于:
\prod_{n=1}^{\infty}(1-q^{2n})^{-1}\sum_{l\in\mathbb Z}x^{2l}q^{l^2}=\sum_{l\in\mathbb Z}\sum_{n=0}^{\infty}p(n)x^{2l}q^{2n+l^2}
而左边:
\prod_{n=1}^{\infty}(1+x^2q^{2n-1})(1+x^{-2}q^{2n-1})=\left(\sum_{r=0}^{\infty}\sum_{i=0}^{\infty}p_{od}(i,r)x^{2r}q^i\right)\left(\sum_{r=0}^{\infty}\sum_{i=0}^{\infty}p_{od}(i,r)x^{-2r}q^i\right)
比较 x^{2l} 的系数,只需证:
\sum_{n=0}^{\infty}p(n)q^{2n+l^2}=\sum_{r=0}^{\infty}\left(\sum_{i=0}^{\infty}p_{od}(i,r)q^i\right)\left(\sum_{i=0}^{\infty}p_{od}(i,l+r)q^i\right)
比较 q^{2n+l^2} 的系数,化为:
p(n)=\sum_{r=0}^{\infty}\sum_{i=0}^{2n+l^2}p_{od}(i,r)p_{od}(2n+l^2-i,l+r)
此即上文所得结论,故原式成立。
这个柿子可用于表示 Jacobi \vartheta 函数的展开:
\vartheta(z,q)=\sum_{n\in\mathbb Z}q^{n^2}\text{e}^{2\pi\text{i}nz}
用 w=\text{e}^{\pi\text{i}z} 代替 z :
\vartheta(z,q)=\sum_{n\in\mathbb Z}w^{2n}q^{n^2}
这就是 Jacobi 三重积恒等式的形式,有:
\begin{aligned}
\vartheta(z,q)&=\prod_{n=1}^{\infty}(1-q^{2n})(1+w^2q^{2n-1})(1+w^{-2}q^{2n-1})\\
&=\prod_{n=1}^{\infty}(1-q^{2n})(1+(w^2+w^{-2})q^{2n-1}+q^{4n-2})\\
&=\prod_{n=1}^{\infty}(1-q^{2n})(1+2\cos(2\pi z)q^{2n-1}+q^{4n-2})
\end{aligned}
Jacobi \vartheta 函数和平方和分拆(P2019)等都有紧密联系。
§1.3 分拆数的四种求法
我们想要得到比 \mathcal O(n^2) 更优秀的计算分拆数的方法(P6189)。
ln-exp
观察 \widetilde{p} 的形式,可以想到使用 ln-exp 方法:
\begin{aligned}
\widetilde{p}(x)&=\prod_{i=1}^{\infty}\dfrac{1}{1-x^i}\\
&=\exp\left(-\sum_{i=1}^{\infty}\ln(1-x^i)\right)
\end{aligned}
现在要快速求出 \sum 里的东西,乱推一波。(一年前射出的子弹正中眉心)
设 f_n(x)=\ln(1-x^n) ,两边同时求导有 f_n'(x)=\dfrac{(1-x^n)'}{1-x^n}=-\dfrac{nx^{n-1}}{1-x^n} 。
由 \dfrac{1}{1-x^n}=\sum\limits_{i=0}^{\infty}x^{in} 得 f_n'(x)=-\sum\limits_{i=1}^{\infty}nx^{in-1} ,再积回去就有 f_n(x)=-\sum\limits_{i=1}^\infty\dfrac{x^{in}}{i} 。
因此 \ln(1-x^n) 的系数只会在 n 的倍数次幂处有值,枚举倍数即可在 \mathcal O(n\log n) 的时间复杂度内求出 \sum 里的东西,然后可以使用 \mathcal O(n\log^2 n) 或者 \mathcal O(n\log n) 的多项式 exp 求解。
如果模数比较舒适(例如 998244353 这种 NTT 模数)就直接做完了,但如果不是 NTT 模数,甚至不是素数,就需要一些更通用的方法。
根号分治
分拆数本质上是一种完全背包方案数,有一个根号分治做法。
设 B=\lfloor\sqrt n\rfloor 。对于 i<B ,直接用完全背包,设 f_{i,j} 表示考虑了 1\sim i 的数,总和为 j 的方案数,转移方程为 f_{i,j}=f_{i-1,j}+f_{i,j-i} ,这部分复杂度为 \mathcal O(n\sqrt n) 。
对于 i\ge B ,总个数为 \mathcal O(\sqrt n) 级别,有另一个 dp:设 g_{i,j} 表示用了 i 个 \ge B 的数,总和为 j 的方案数,转移时由于需要确保不递增的顺序,有两种方式:在末尾新增一个 B ,以及整体加一,故转移方程为 g_{i,j}=g_{i-1,j-B}+g_{i,j-i} ,复杂度也为 \mathcal O(n\sqrt n) 。
求解 p(n) 时,设 F_j=f_{B-1,j},G_j=\sum\limits_{i=0}^{\lfloor n/B\rfloor}g_{i,j} ,答案即为 \sum\limits_{i=0}^{n}F_iG_{n-i} 。如果只求一个的话可以直接算,要求 1\sim n 每个数的分拆数的话还需要做卷积。
五边形数定理
考察 \widetilde{p}^{-1}(x)=\phi(x)=\prod\limits_{i=1}^{\infty}(1-x^i) 的系数。
定理 1.3.1(Euler 五边形数定理)
\phi(x)=\sum\limits_{n\in\mathbb Z}(-1)^nx^{(3n^2-n)/2}
在 Jacobi 三重积恒等式中令 q=-z^3 ,有:
\begin{aligned}
\prod_{n=1}^{\infty}(1-z^{6n})(1+z\cdot(-z^{6n-3}))(1+z^{-1}\cdot(-z^{6n-3}))&=\prod_{n=1}^{\infty}(1-z^{6n})(1-z^{6n-2})(1-z^{6n-4})\\
&=\prod_{n=1}^{\infty}(1-(z^2)^n)=\sum_{n\in\mathbb Z}(-1)^nz^{3n^2+n}
\end{aligned}
令 x=z^2 ,就得到 \phi(x) 的展开式 \sum\limits_{n\in\mathbb Z}(-1)^nx^{(3n^2-n)/2} (为了契合“五边形数”的名字,这里改记 +n 为 -n )。
得到该结果后,考虑利用其求出 \widetilde{p}(x) :
\phi(x)\widetilde{p}(x)=(1-x-x^2+x^5+\dots)(1+p(1)x+p(2)x+\dots)=1
比较系数,可得:
p(n)-p(n-1)-p(n-2)+p(n-5)+p(n-7)-\dots=0
五边形数是 \mathcal O(n^2) 级别的,因此可以直接使用该递推式计算,时间复杂度为 \mathcal O(n\sqrt n) 。
Durfee Square
类比之前的想法,对于任意一个点数为 n 的 Ferrers 图,找到其内部以左上角为顶点的最大正方形,称其为该 Ferrers 图的 Durfee Square,设其边长为 r 。
去掉该正方形后,原图会被分成两个子图,行数不超过 r ,其点数和为 n-r^2 ,容易发现这是一个双射,故有:
\prod_{i=1}^{\infty}\dfrac{1}{1-x^i}=\sum_{r=0}^{\infty}x^{r^2}\left(\prod_{i=1}^r\dfrac{1}{1-x^i}\right)^2
由于 r^2\le n ,我们只需要 1\sim\sqrt n 中的 r 就能计算出前 n 项的值,时间复杂度为 \mathcal O(n\sqrt n) 。
§1.4 对分拆数的估计
我们现在可以得到关于分拆数上界的粗略结果。
定理 1.4.1
p(n)<\exp\left(\sqrt{\dfrac{2n}3}\pi\right)
考察 \ln\widetilde{p}(x) ,将其在 x=0 处 Taylor 展开得到其 Maclaurin 级数(其实这也就是上面 ln-exp 得到的结果):
\begin{aligned}
\ln\widetilde{p}(x)&=-\sum\limits_{n=1}^{\infty}\ln(1-x^n)\\
&=-\sum_{n=1}^{\infty}\left(-\sum_{i=1}^{\infty}\dfrac{x^{ni}}{i}\right)\\
&=\sum_{n=1}^{\infty}\dfrac1n\cdot\dfrac{x^n}{1-x^n}\\
&=\sum_{n=1}^{\infty}\dfrac1n\cdot\dfrac{x}{1-x}\cdot\dfrac{x^{n-1}}{1+x+\dots+x^{n-1}}
\end{aligned}
级数在 |x|<1 时收敛,这时 1>x>\dots>x^n ,有 1+x+\dots+x^{n-1}>nx^{n-1} ,因此 \dfrac{x^n}{1-x^n}<\dfrac 1n\cdot\dfrac{x}{1-x} ,有:
\ln\widetilde{p}(x)<\sum_{n=1}^{\infty}\dfrac{1}{n^2}\cdot\dfrac{x}{1-x}=\dfrac{\pi^2}{6}\cdot\dfrac{x}{1-x}
又因为 \ln\widetilde{p}(x)>\ln(p(n)x^n)=\ln p(n)+n\ln x ,即 \ln p(n)<\ln\widetilde{p}(x)+n\ln\dfrac1x ,可以得到:
\ln p(n)<\dfrac{\pi^2}{6}\cdot\dfrac{x}{1-x}+n\ln\dfrac1x
使用放缩 \ln x\le x-1 ,有 \ln p(n)<\dfrac{\pi^2}{6}\cdot\dfrac{x}{1-x}+n\left(\dfrac 1x-1\right)=F(x) ,欲寻找 F 的最小值,令 F'(x)=0 ,有:
F'(x)=\dfrac{\pi^2}{6}\cdot\dfrac{1}{(1-x)^2}-\dfrac{n}{x^2}=0\Rightarrow\left(6n-\pi^2\right)x^2-12nx+6n=0
解这个方程,得 x=\dfrac{6n\pm\sqrt{6n}\pi}{6n-\pi^2} ,取 <1 的解,即 x=\dfrac{6n-\sqrt{6n}\pi}{6n-\pi^2}=\dfrac{\sqrt{6n}}{\sqrt{6n}+\pi} ,代入 F 可得 \ln(p(n))<\sqrt{\dfrac{2n}3}\pi ,即 p(n)<\exp\left(\sqrt{\dfrac{2n}3}\pi\right) 。
证明过程中放缩了很多次,可以看到这个上界还是太宽了!实际上可以通过椭圆模函数等方法得出分拆数的渐进公式:p(n)\sim\dfrac{1}{4\sqrt3n}\exp\left(\sqrt{\dfrac{2n}3}\pi\right) ,显然这个东西还是超出了我目前的知识水平。。。
关于分拆数,差不多就说到这里。
二.q -模拟
§2.1 基础对象的 q -模拟
为什么会有 q -模拟(即 q -analog)这个东西?其想法在于,对于函数 f 或者别的什么东西,给她加上 q 这一维变成 f_q ,满足 \lim\limits_{q\rightarrow 1}f_q=f ,而 q 可以是具体的取值,也可以看作是形式幂级数的变元。
而把 q -analog 视作形式幂级数时,q^n 的系数其实可以视作统计量为 n 的计数对象的贡献和,令 q=1 就得到所有计数对象的贡献和,因此 q -analog 有时可以帮助研究组合类中元素的分布。这段话乍看会比较莫名其妙,后面会给出一些具体的解释。
定义 2.1.1
定义 \bm q -上升阶乘 为:
\begin{aligned}
(a;q)_\infty&=\prod_{i=1}^\infty(1-aq^i)\\
(a;q)_n&=\dfrac{(a;q)_\infty}{(aq^n;q)_\infty}
\end{aligned}
当 n 为正整数时,定义等价于 (a;q)_n=\prod\limits_{i=0}^{n-1}(1-aq^i) (而且比较常用的貌似也是这个定义)。
记 (a_1,\dots,a_k;q)_n=(a_1;q)_n\dots(a_k;q)_n 。
例如定理 1.1.4 就可以表示为 (-q;q)_{\infty}=(q;q^2)_\infty^{-1} ,Jacobi 三重积恒等式可以记为 (-zq;q^2)_\infty(-q/z;q^2)_\infty(q^2;q^2)_\infty=\sum\limits_{n\in\mathbb Z}z^nq^{n^2} 。
为了构造各种对象的 q -analog,首先需要定义数与阶乘的 q -analog:
定义 2.1.2
定义数 \bm n 的 \bm q -analog 为 [n]_q=\dfrac{1-q^n}{1-q} ,容易验证 \lim\limits_{q\rightarrow 1}[n]_q=n 。
对于正整数 n ,定义 \bm q -阶乘 为:
[n]_q!=\prod_{i=1}^n[i]_q=\dfrac{(q;q)_n}{(1-q)^n}
同样还能对 n\in\mathbb R,m\in\mathbb Z 定义 [n]_q^{\overline{m}}=[n]_q[n+1]_q\dots[n+m-1]_q 和 [n]_q^{\underline{m}}=[n]_q[n-1]_q\dots[n-m+1]_q 。
再回头看前面那段莫名其妙的话,在这里我们相当于对于正整数 n ,设 S=[0,n-1]\cap\mathbb Z ,\forall i\in S ,定义了统计量 f(i)=i ,这样就有 [n]_q=\sum\limits_{i\in S}q^{f(i)}=\dfrac{1-q^n}{1-q} 。
这也提供了一种视角:对于一个 q -analog,考虑其对应的统计量的组合意义。那我们不妨来考量 [n]_q! 对应的组合意义是什么。
定理 2.1.3
对于长度为 n 的排列 \sigma ,定义 \text{inv}(\sigma) 为 \sigma 的逆序对个数,\text{maj}(\sigma) 为 1\sim n-1 中所有满足 \sigma_i>\sigma_{i+1} 的 i 之和,有:
\sum_{\sigma\in P_n}q^{\text{inv}(\sigma)}=\sum_{\sigma\in P_n}q^{\text{maj}(\sigma)}=[n]_q!
证明:对于 \text{inv} ,容易想到设 \sigma' 为 \sigma 去掉 n 后得到的排列,考虑 n 插入的位置,有:
\begin{aligned}
\sum_{\sigma\in P_n}q^{\text{inv}(\sigma)}&=\sum_{\sigma'\in P_{n-1}}\sum_{i=0}^{n-1}q^{i+\text{inv}(\sigma')}\\
&=\sum_{i=0}^{n-1}q^i\sum_{\sigma'\in P_{n-1}}q^{\text{inv}(\sigma')}\\
&=[n]_q\sum_{\sigma'\in P_{n-1}}q^{\text{inv}(\sigma')}
\end{aligned}
这样递归下去就得到 [n]_q[n-1]_q\dots[2]_q\sum\limits_{\sigma\in P_1}q^{\text{inv}(\sigma)}=[n]_q! 。
对于 \text{maj} ,可以发现插入 n 时 \text{maj} 的变化量也恰好取遍 0\sim n-1 ,因此证明和上面是一样的。
对于组合类 \mathcal A 及 \mathcal A 到 \mathbb Z 的函数 f ,可以看出 \sum\limits_{a\in\mathcal A}q^{f(a)} 就是 \mathcal A 用 f 定义的 OGF,记作 A_f(q) 。当 \mathcal A=P_n 时,若 A_f(q)=[n]_q! ,则称 f 为 Mahonian 的 。
下面定义二项式系数的 q -analog。
定义 2.1.4
对于 n\in\mathbb R,m\in\mathbb Z ,定义 \bm q -二项式系数 为:
{n\brack m}_q=\left\{
\begin{aligned}
&\dfrac{(q^{n-m+1};q)_m}{(q;q)_m}\quad&m\ge 1\\
&1&m=0\\
&0&m<0
\end{aligned}
\right.
当 n,m\in\mathbb N 且 n\ge m 时,有 \begin{bmatrix}n\\m\end{bmatrix}_q=\begin{bmatrix}n\\n-m\end{bmatrix}_q=\dfrac{[n]_q!}{[n-m]_q![m]!} 。
既然有了 q -二项式系数,自然想要把二项式系数上的一些柿子推广到 q -二项式系数上,有:
定理 2.1.5 ~ 2.1.8
对于 n,m,k\in\mathbb N ,有:
{n\brack m}_q=q^m{n-1\brack m}_q+{n-1\brack m-1}_q={n-1\brack m}_q+q^{n-m}{n-1\brack m-1}_q
\sum_{i=0}^nq^{\binom i2}{n\brack i}_qx^i=\prod_{i=0}^{n-1}(1+xq^i)
{m+n\brack k}_q=\sum_{i=0}^kq^{(m-i)(q-i)}{m\brack i}_q{n\brack k-i}_q
{m+n+1\brack n+1}_q=\sum_{i=0}^mq^i{n+i\brack n}_q
都可以使用归纳法证明,在此不做赘述。而 q -Vandermonde 卷积有一个有趣的组合意义,在那之前需要先引出 q -二项式系数的组合意义:
定理 2.1.9
直接把转移式写出来,使用 q -Pascal 恒等式即可证明。
因此容易看出 q -Vandermonde 卷积就是把长度为 m+n 且有 k 个 1 的 01 串分成长度为 m 和 n 的两部分,再枚举第一部分有多少个 1 ,再补上跨越的逆序对数。
当 q 为具体取值时,q -二项式系数还有其特殊的组合意义:
定理 2.1.10
对于素数幂 q ,设 V 为域 \mathbb F_q 上的 n 维线性空间,则 V 的 k 维子空间个数为 \begin{bmatrix}n\\k\end{bmatrix}_q 。
证明:V 的一个 k 维子空间可以由 V 中的线性无关向量组 a_1,\dots,a_k 生成,而 a_1 有 q^n-1 种选法(要求 a_1\neq \bm 0 ),a_2 有 q^n-q 种选法(和 a_1 线性无关),以此类推,共 \prod\limits_{i=0}^{k-1}(q^n-q^i) 种选法。
而对于一个 k 维子空间,同理可得其有 \prod\limits_{i=0}^{k-1}(q^k-q^i) 种生成方式,因此子空间个数为:
\begin{aligned}
\dfrac{\prod\limits_{i=0}^{k-1}(q^n-q^i)}{\prod\limits_{i=0}^{k-1}(q^k-q^i)}&=\dfrac{\prod\limits_{i=n-k+1}^n(q^i-1)}{\prod\limits_{i=1}^k(q^i-1)}\\
&=\dfrac{[n]_q!}{[n-k]_q![k]!}={n\brack k}_q
\end{aligned}
类似二项式反演地,有 q -二项式反演(Gauss 反演):
定理 2.1.11(Gauss 反演)
b_n=\sum_{k=0}^n{n\brack k}_qa_k\Leftrightarrow a_n=\sum_{k=0}^n(-1)^{n-k}q^{\binom{n-k}2}{n\brack k}_qb_k
容易通过观察消元时各项的系数得到该结论,也可以直接代回证明。
考虑构造 2^n 的 q-analog,一种方式是定义 2^{[n]_q}=\sum\limits_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}_q (注意这也许是一个不标准的记号),那么 [q^c]2^{[n]_q} 即为所有长度为 n 的 01 串中恰有 c 个逆序对的串个数,容易发现 2^{[n]_q}-2^{[n-1]_q}=\sum\limits_{k=0}^{n-1}q^{n-k-1}\begin{bmatrix}n-1\\k\end{bmatrix}_q=\Delta2^{[n]_q} 。通过乘/除 1-q^m 状物从 \begin{bmatrix}n\\k\end{bmatrix}_q 递推到 \begin{bmatrix}n\\k+1\end{bmatrix}_q ,容易做到在 \mathcal O(n^3) 的时间复杂度内计算 2^{[n]_q} 。
为了进一步拓展,需要定义 q -多项式系数:
定义 2.1.12
对于 n,a_1,\dots,a_m\in\mathbb N 且 \sum\limits_{i=1}^ma_i=n ,定义 \bm q -多项式系数 为:
\begin{bmatrix}n\\a_1,\dots,a_m\end{bmatrix}_q=\dfrac{[n]_q!}{[a_1]_q!\dots[a_m]_q!}
定义 \bm q -幂 为:
m^{[n]_q}=\sum_{a_1+\dots+a_m=n}\begin{bmatrix}n\\a_1,\dots,a_m\end{bmatrix}_q
类比 q -二项式系数的组合意义,对于 q -多项式系数有:
定理 2.1.13
证明是类似的,在此略过。
因此 [q^c]m^{[n]_q} 的组合意义为所有长度为 n 、值域为 [1,m]\cap\mathbb Z 的序列中恰有 c 个逆序对的个数,显然有 \lim_{q\rightarrow 1}m^{[n]_q}=m^n 。
还能够定义 Γ 函数、积分、超几何函数等对象的 q -analog,但与本文主题关系不大,在此略去。(所以本文有主题吗)
这部分的练习题:CF1603F & ARC139F。
§2.2 q -Lucas
为什么要把 q -Lucas 定理单独拿出来作为一节呢,这个东西确实比上面提到的其它关于 q -二项式系数的性质复杂,并且从中也能看出 q -analog 与分圆多项式的一些关系。
现在要找到 Lucas 定理在 q -analog 中的类比,首先观察 Lucas 定理的证明过程,发现其用到了如下性质:\dbinom{p}{m}\equiv[m=0\vee m=p]\pmod p ,我们需要为 q -二项式系数找到类似的性质。对于 \begin{bmatrix}n\\m\end{bmatrix}_q=\dfrac{(q^{n-m+1};q)_m}{(q;q)_m} ,当 0<m<n 时,分子上的 1-q^n 一定会保留(考虑每个分圆多项式 \Phi_d(q) 的次数),只要 p\mid1-q^n\Rightarrow q^n\equiv 1\pmod p 即可。
因此令 d=\delta_p(q) ,得到了如下结论:
引理 2.2.1
{d\brack m}_q\equiv[m=0\vee m=d]\pmod p
现在由 q -二项式定理可以直接得到:
引理 2.2.2
\prod_{i=0}^{d-1}(1+q^ix)=\sum_{i=0}^nq^{\binom i2}{n\brack i}_qx^i\equiv1+q^{\binom d2}x^d\equiv1+(-1)^{[2\mid d]}x^d\pmod p
然后依葫芦画瓢,仿照普通 Lucas 定理的证明写出对应的 q -analog:
\begin{aligned}
[x^m]\prod_{i=0}^{n-1}(1+q^ix)&\equiv[x^m]\left(\prod_{i=0}^{d-1}(1+q^ix)\right)^{\lfloor n/d\rfloor}\prod_{i=0}^{n\bmod d-1}(1+q^ix)\\
&\equiv[x^m]\left(1+(-1)^{[2\mid d]}x^d\right)^{\lfloor n/d\rfloor}\prod_{i=0}^{n\bmod d-1}(1+q^ix)\\
&\equiv[x^{\lfloor m/d\rfloor}]\left(1+(-1)^{[2\mid d]}x\right)^{\lfloor n/d\rfloor}[x^{m\bmod d}]\prod_{i=0}^{n\bmod d-1}(1+q^ix)
\end{aligned}
现在比较系数,有:
q^{\binom m2}{n\brack m}_q\equiv(-1)^{[2\mid d]\lfloor m/d\rfloor}\binom{\lfloor n/d\rfloor}{\lfloor m/d\rfloor}q^{\binom{m\bmod d}{2}}{n\bmod d\brack m\bmod d}_q\pmod p
分 d 的奇偶性讨论,若 2\nmid d ,此时有 \dbinom m2\equiv\dbinom{m\bmod d}{2}\pmod d ,因此有 \begin{bmatrix}n\\m\end{bmatrix}_q\equiv\dbinom{\lfloor n/d\rfloor}{\lfloor m/d\rfloor}\begin{bmatrix}n\bmod d\\m\bmod d\end{bmatrix}_q\pmod p 。
若 2\mid d ,仍然考虑两边 q 的次数,有 \dbinom m2-\dbinom{m\bmod d}{2}=\dfrac12m(m-1)-\dfrac12(m-d\lfloor m/d\rfloor)(m-d\lfloor m/d\rfloor-1)=\dfrac{d^2\lfloor m/d\rfloor^2}{2}+\dfrac{d(2m-1)\lfloor m/d\rfloor}{2} ,前者是 d 的倍数,而通过分讨 \lfloor m/d\rfloor 的奇偶性,可以发现后者恰好与 (-1)^{\lfloor m/d\rfloor} 相抵消,因此我们得到了如下结论:
定理 2.2.3
\begin{bmatrix}n\\m\end{bmatrix}_q\equiv\dbinom{\lfloor n/d\rfloor}{\lfloor m/d\rfloor}\begin{bmatrix}n\bmod d\\m\bmod d\end{bmatrix}_q\pmod p
上面的证明过程中用到的引理 2.2.1 需要 $q^n=1$,除了在模 $p$ 意义下寻找 $q$ 的阶以外,还可以让 $q$ 发挥主观能动性,令 $q=\omega_d^k$ 为一个 $d$ 次本原单位根,此时仍然有上式成立。
而分圆多项式 $\Phi_d(q)$ 的全体根即为全体 $d$ 次本原单位根,因此我们有:
> **定理 2.2.4**
>
> $$
> \begin{bmatrix}n\\m\end{bmatrix}_q\equiv\dbinom{\lfloor n/d\rfloor}{\lfloor m/d\rfloor}\begin{bmatrix}n\bmod d\\m\bmod d\end{bmatrix}_q\pmod{\Phi_d(q)}
> $$
这部分的练习题:LOJ562。
### §2.3 $q$-Catalan
$q$-Catalan 有两种常见的定义方式,首先需要定义 Dyck 路:
> **定义 2.3.1**
>
> 定义阶为 $n$ 的 **Dyck 路** $\Pi$ 是一条二维平面上的路,其起点为 $(0,0)$,终点为 $(n,n)$,每一步只能往 $+x$ 或 $+y$ 方向走 $1$ 格,且任何时刻 $x\le y$。记阶为 $n$ 的全体 Dyck 路的集合为 $D_n$。
>
> 如 $n=4$ 时的一条 Dyck 路: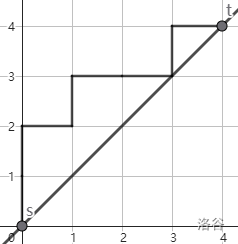
>
> 定义 **Dyck 路的 Area 统计量** $\text{area}(\Pi)$ 为 $\Pi$ 和主对角线 $y=x$ 中所夹的**完整方格**个数,如上图中有 $\text{area}(\Pi)=2$。
>
> 定义 Catalan 数的 $q$-analog 为 $C_n(q)=\sum\limits_{\Pi\in D_n}q^{\text{area}(\Pi)}$。
Dyck 路可以和长度为 $2n$ 且有 $n$ 个 $0$ 的 $01$ 串建立映射:将 $+y$ 方向走的一步映成 $0$,将 $+x$ 方向走的一步映成 $1$。
如上定义的 $q$-Catalan 数具有如下性质:
> **定理 2.3.2**
>
> $$
> C_n(q)=\sum_{k=0}^{n-1}q^kC_k(q)C_{n-k-1}(q)
> $$
证明:考虑 Dyck 路 $\Pi$ 第一次碰到对角线的位置 $(k,k)$,将 $\Pi$ 在 $(k,k)$ 之前的片段整体往右下移动一个单位即可得到一个 $k-1$ 阶 Dyck 路,并且减少了 $k-1$ 个完整方格,由 OGF 乘法的组合意义得贡献为 $q^{k-1}C_{k-1}(q)C_{n-k}(q)$,因此原式成立。
另一种更常见的定义如下:
> **定义 2.3.3**
>
> 定义 $\bm q$**-Catalan** 为:
> $$
> \text{Cat}(n)_q=\dfrac{1}{[n+1]_q}\begin{bmatrix}2n\\n\end{bmatrix}_q=\begin{bmatrix}2n\\n\end{bmatrix}_q-q\begin{bmatrix}2n\\n+1\end{bmatrix}_q
> $$
这个定义相当于是直接由原对象(Catalan 数)的定义式转写得到的,自然要问,这个东西在计数什么?
首先按照上面提到的映射,一个 $n$ 阶 Dyck 路 $\Pi$ 可以被映射成一个长度为 $2n$、恰有 $n$ 个 $0$ 的 $01$ 串,满足前缀 $0$ 个数 $\ge$ 前缀 $1$ 个数,据此可以定义 $\Pi$ 的降位和 $\text{maj}(\Pi)$。
有结论:
> **定理 2.3.4**
>
> $$
> \text{Cat}(n)_q=\sum_{\Pi\in D_n}q^{\text{maj}(\Pi)}
> $$
证明:首先在 $n$ 阶非 Dyck 路和 $(0,0)$ 到 $(n-1,n+1)$ 的全体格路之间建立双射:对于 $n$ 阶非 Dyck 路 $\Pi$,找到其 $x-y$ 最大的格点 $P$(若有多个选择最前面的一个),设其前一个格点为 $Q$,将 $PQ$ 之间的边由横着变为竖着,体现在 $\Pi$ 对应的 $01$ 串上就是把 $11$ 修改为 $10$,对 $\text{maj}(\Pi)$ 的影响就是减少 $1$,容易发现这是一个双射。
设全体长为 $2n$,有 $n+1$ 个 $0$ 的 $01$ 串构成的集合为 $S$,有:
$$
\sum_{\Pi\in\{0,1\}^n\setminus D_n}q^{\text{maj}(\Pi)}=\sum_{\Pi\in S}q^{\text{maj}(\Pi)+1}=q\begin{bmatrix}2n\\n+1\end{bmatrix}_q
$$
那么有:
$$
\sum_{\Pi\in D_n}q^{\text{maj}(\Pi)}=\begin{bmatrix}2n\\n\end{bmatrix}_q-q\begin{bmatrix}2n\\n+1\end{bmatrix}_q=\text{Cat}(n)_q
$$
### §2.4 $q$-导数
都 $q\rightarrow 1$ 了,不顺便定义一个 $q$-导数说不过去吧!
> **定义 2.4.1**
>
> 定义函数 $f$ 的 $\bm q$**-微分** $\text{d}_qf$ 为 $f(qx)-f(x)$。定义 $f$ 的 $\bm q$**-导数**为:
>
> $$
> \mathcal D_qf(x)=\dfrac{\text{d}_qf}{\text{d}_qx}=\dfrac{f(qx)-f(x)}{qx-x}
> $$
当 $f$ 在 $x_0$ 处可导时,有 $\lim\limits_{q\rightarrow 1}\mathcal D_qf(x_0)=f'(x_0)$。
下面举几个具体的例子。
1. $\mathcal D_qx^n=\dfrac{q^nx^n-x^n}{qx-x}=\dfrac{q^n-1}{q-1}\cdot x^{n-1}=[n]_qx^{n-1}$;
2. $\mathcal D_q\ln x=\dfrac{\ln qx-\ln x}{qx-x}=\dfrac{\ln q}{qx-x}$;
3. 定义 $\bm q$**-指数**为 $\text{e}_q^x=\sum\limits_{n=0}^\infty\dfrac{x^n}{[n]_q!}$,易知 $\mathcal D_q\text{e}_q^x=\text{e}_q^x$;
4. 定义 $\bm q$**-正弦函数**和 $\bm q$**-余弦函数**为 $\sin_q(x)=\dfrac{\text{e}_q^{\text{i}x}-\text{e}_q^{-\text{i}x}}{2\text{i}}$,$\cos_q(x)=\dfrac{\text{e}_q^{\text{i}x}+\text{e}_q^{-\text{i}x}}2$,容易得出 $\mathcal D_q\sin_q(x)=\cos_q(x)$,$\mathcal D_q\cos_q(x)=-\sin_q(x)$。
类比离散微积分,记 $\text{E}_qf(x)=f(qx)$,类似导数,$q$-导数有类似的性质:
1. $\mathcal D_qCf=C\mathcal D_qf$;
2. $\mathcal D_q(f+g)=\mathcal D_qf+\mathcal D_qg$;
3. $\mathcal D_q(fg)=f\mathcal D_qg+\text{E}_qg\mathcal D_qf=\text{E}_qf\mathcal D_qg+g\mathcal D_qf$;
4. $\mathcal D_q\left(\dfrac1f\right)=-\dfrac{\mathcal D_qf}{f\text{E}_qf}$;
5. $\mathcal D_q\left(\dfrac fg\right)=\dfrac{\text{E}_qg\mathcal D_qf-\text{E}_qf\mathcal D_qg}{g\text{E}_qg}$;
6. $\mathcal D_qf(Cx)=C(\mathcal D_qf)(Cx)$。
(运算符优先级可能会有点令人迷惑,这里的每个算子只结合其右边紧挨着的那一个量或括号)
证明均很简单,在此不做赘述。正如离散微积分,难以写出 $q$-导数的链式法则。
对于普通的求导 $\mathcal D$,有高阶导数的 Leibniz 公式 $\mathcal D^n(uv)=\sum\limits_{k=0}^n\dbinom nk\mathcal D^ku\mathcal D^{n-k}v$,其也有对应的 $q$-analog 版本:
> **定理 2.4.1($\bm q$-Leibniz 公式)**
>
> $$
> \mathcal D_q^n(uv)=\sum_{k=0}^n{n\brack k}_q\mathcal D_q^{n-k}\text{E}_q^ku\mathcal D_q^kv
> $$
考虑使用数学归纳法,狂暴拆开:
$$
\begin{aligned}
\mathcal D_q(\mathcal D_q^n(uv))&=\mathcal D_q\left(\sum_{k=0}^n{n\brack k}_q\mathcal D_q^{n-k}\text{E}_q^ku\mathcal D_q^kv\right)\\
&=\sum_{k=0}^n{n\brack k}_q\mathcal D_q(\mathcal D_q^{n-k}\text{E}_q^ku\mathcal D_q^kv)\\
&=\sum_{k=0}^n{n\brack k}_q(q^k\mathcal D_q^{n-k+1}\text{E}_q^ku\mathcal D_q^kv+\mathcal D_q^{n-k}\text{E}_q^{k+1}u\mathcal D_q^{k+1}v)\\
&=\sum_{k=0}^n{n\brack k}_qq^k\mathcal D_q^{n-k+1}\text{E}_q^ku\mathcal D_q^kv+\sum_{k=0}^n{n\brack k}_q\mathcal D_q^{n-k}\text{E}_q^{k+1}u\mathcal D_q^{k+1}v\\
&=\sum_{k=0}^{n+1}{n\brack k}_qq^k\mathcal D_q^{n-k+1}\text{E}_q^ku\mathcal D_q^kv+\sum_{k=0}^{n+1}{n\brack k-1}_q\mathcal D_q^{n-k+1}\text{E}_q^ku\mathcal D_q^kv\\
&=\sum_{k=0}^{n+1}{n+1\brack k}_q\mathcal D_q^{n-k+1}\text{E}_q^ku\mathcal D_q^kv=\mathcal D_q^{n+1}(uv)
\end{aligned}
$$
故原式成立。
---
本文的内容就到此为止了,其实这篇文章只能算一个引子,分拆数和 $q$-analog 能引出的内容还有很多,譬如平方分拆、量子群、$q$-变形代数等。对于超几何级数,其 $q$-analog——基本超几何级数,随着其研究的不断深入,已日渐显现出其重要性,在数论、李代数甚至物理学中都有重要的应用。
那么就到这里,拜拜。