题解:P11657 「FAOI-R5」datealive
immix
·
·
题解
更好的体验
类似题目:
- P10513 括号
- P8765 [蓝桥杯 2021 国 AB] 翻转括号序列
区间翻转,区间最长合法括号子串
P11657 「FAOI-R5」datealive
给定一个长度为 n 的括号序列,支持 m 次操作:
- 翻转 [l,r] 中的括号,即
( 变 ),) 变 (。
- 查询子串 [l,r] 最长合法括号子串的长度。
对于翻转来说。我们只用额外维护一个节点保存取反之后的结果,然后翻转操作交换两个节点的内容,不是本题的难点,我们考虑如何求出一个区间的最长合法括号子串。
利用线段树的分治结构,我们能求出了只在左右区间内的结果,考虑如何处理横跨区间两边的子串。
我们知道:一个括号序列能匹配都匹配完之后剩下一定是一段前缀 `)` 和后缀 `(`。(要不然就还有能匹配的部分)
比如序列 `(())))()(()` 最后留下的就是 `))(`。
不失一般性,假设左区间在右边剩下的 `(` 个数更多。
假设匹配了 $k$ 个,我们只需要找到左区间简化后的第 $k+1$ 个 `(`(从右边数)和右边的第一个 `(`(从左边数)。
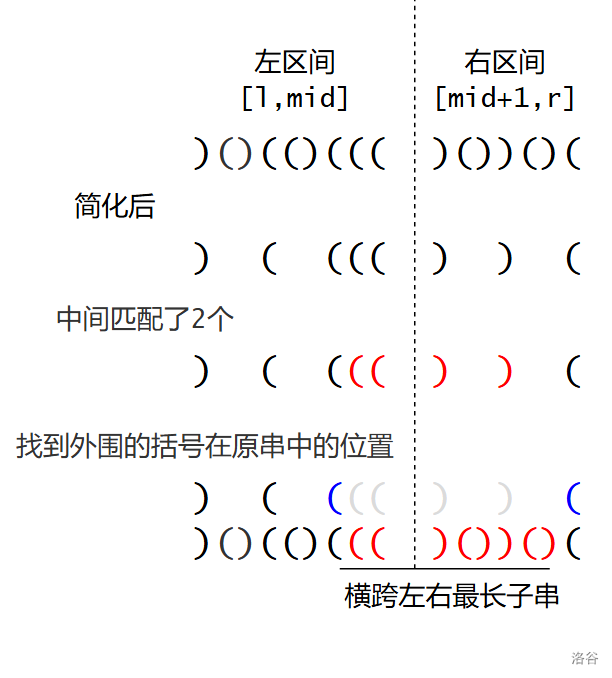
我们讨论实现找到这些括号位置的细节。
我们发现,对于一个固定起点来说,开头剩余的 `)` 个数单调不下降。(因为再也没有字符能和它匹配了)
同样地,对于一个固定终点来说,结尾剩余的 `(` 个数也单调不下降。
基于这个单调性,我们可以用线段树二分,花费 $O(\log n)$ 的代价找到这些括号的位置。
对于 `)` 来说,因为是固定起点单调不降,所以只能左往右找到第 $k$ 个 `)`(如果反过来,`)` 就有可能被前面的 `(` 闭合,难以找到实际的位置) ,而对于 `(` 就只能从右往左找了。
直接线段树二分也是可行的,这里提供一种更简单的二分。
对于区间 $[l,r]$ 和一个完全包含它的节点 $o$:
先花 $O(\log n)$ 把 $[l,r]$ 拆分成 $O(\log n)$ 个区间。
```cpp
struct Node{
int o,l,r; // 包含 [l,r] 的线段树节点编号和该节点维护区间
int cntL,cntR,ans; // 左边剩下的),右边剩下的(,答案
};
Node stk[10000];int tp;
void find_nodes(int o,int ql,int qr,int op){
if(ql<=t[o][op].l&&t[o][op].r<=qr){stk[++tp]=t[o][op];return;}
int lch=o<<1,rch=o<<1|1;
int mid=(t[o][op].l+t[o][op].r)>>1;
pushdown(o);
if(ql<=mid)find_nodes(lch,ql,qr,op);
if(qr> mid)find_nodes(rch,ql,qr,op);
}
```
然后以找到从左边数第 $k$ 个 `)` 为例:
找到 $O(\log n)$ 段中第一个达到 $k$ 个 `)` 的,然后在这一段里面进行二分找到真正的分界点,这样二分就保证了时刻处理的都一定是完整的节点,直接用一个 `while` 循环就足够解决问题。
复杂度仍然是 $O(\log n)$。
```cpp
struct Node{
int o,l,r; // 包含 [l,r] 的线段树节点编号和该节点维护区间
int cntL,cntR,ans; // 左边剩下的),右边剩下的(,答案
};
// 找到 [ql,qr] 中第 k 个剩的右括号所在的位置(最靠左的那个)
int getkth_L(int o,int ql,int qr,int op,int k){
tp=0; find_nodes(o,ql,qr,op);
for(int i=1;i<=tp;i++){
if(stk[i].cntL >= k){ // 在 i 处二分即可。
int l = stk[i].l, r = stk[i].r;
o = stk[i].o;
while(l<r){
pushdown(o); // 记得 pushdown
int mid=(l+r)>>1;
int lch=o<<1,rch=o<<1|1;
if(t[lch][op].cntL >= k)r=mid,o=lch;
else k=k-t[lch][op].cntL+t[lch][op].cntR,l=mid+1,o=rch;
}
return l;
}
k = k - stk[i].cntL + stk[i].cntR;
}
assert(0); // 我们保证一定存在这样的位置
return -1;
}
```
有了这个,我们就可以开始写 `merge` 函数,用于合并两个节点了。
```cpp
Node merge(const Node& p,const Node& q,int op){
int elim = min(p.cntR, q.cntL);
Node ret{min(p.o,q.o)>>1,p.l,q.r,p.cntL+q.cntL-elim,p.cntR+q.cntR-elim,max(p.ans,q.ans)};
int newans;
if(p.cntR == q.cntL){
newans = (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r)
- (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
}
else if(p.cntR >= q.cntL){
// q 的被消耗完了
newans = (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r)
- (getkth_R(p.o,p.l,p.r,op,q.cntL+1)+1) + 1;
}
else{
// p 的被消耗完了
newans = (getkth_L(q.o,q.l,q.r,op,p.cntR+1)-1)
- (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
}
ret.ans = max(ret.ans, newans);
return ret;
}
```
分类讨论哪边的括号被消耗完,找到对应的位置,算出横跨的长度更新答案就好了。
建树复杂度 $T(n)=2T(n/2)+O(\log n) = O(n)$,查询复杂度 $O(\log^2 n)$。
总复杂度 $O(n+q\log^2 n)$。
这道题空间卡的也比较紧(主要是 $n$ 太大了)。
完整代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 4e6+6;
int a[N];
struct Node{
int o,l,r; // 包含 [l,r] 的线段树节点编号和该节点维护区间
int cntL,cntR,ans; // 左边剩下的),右边剩下的(,答案
};
Node t[N*4][2];bool tag[N*4];
void inv(int o){
swap(t[o][0],t[o][1]);
tag[o] = !tag[o];
}
void pushdown(int o){
if(tag[o]){
int lch=o<<1,rch=o<<1|1;
inv(lch);inv(rch);
tag[o]=0;
}
}
Node stk[10000];int tp;
void find_nodes(int o,int ql,int qr,int op){
if(ql<=t[o][op].l&&t[o][op].r<=qr){stk[++tp]=t[o][op];return;}
int lch=o<<1,rch=o<<1|1;
int mid=(t[o][op].l+t[o][op].r)>>1;
pushdown(o);
if(ql<=mid)find_nodes(lch,ql,qr,op);
if(qr> mid)find_nodes(rch,ql,qr,op);
}
// 找到 [ql,qr] 中第 k 个剩的右括号所在的位置(最靠左的那个)
int getkth_L(int o,int ql,int qr,int op,int k){
tp=0; find_nodes(o,ql,qr,op);
for(int i=1;i<=tp;i++){
if(stk[i].cntL >= k){ // 在 i 处二分即可。
int l = stk[i].l, r = stk[i].r;
o = stk[i].o;
while(l<r){
pushdown(o);
int mid=(l+r)>>1;
int lch=o<<1,rch=o<<1|1;
if(t[lch][op].cntL >= k)r=mid,o=lch;
else k=k-t[lch][op].cntL+t[lch][op].cntR,l=mid+1,o=rch;
}
return l;
}
k = k - stk[i].cntL + stk[i].cntR;
}
assert(0);
return -1;
}
// 找到 [ql,qr] 中从右边看,第k个右边剩下的左括号所在的位置(最靠右的那个)
int getkth_R(int o,int ql,int qr,int op,int k){
tp=0; find_nodes(o,ql,qr,op);
for(int i=tp;i>=1;i--){
if(stk[i].cntR >= k){ // 在 i 处二分即可。
int l = stk[i].l, r = stk[i].r;
o = stk[i].o;
while(l<r){
pushdown(o);
int mid=(l+r)>>1;
int lch=o<<1,rch=o<<1|1;
if(t[rch][op].cntR >= k)l=mid+1,o=rch;
else k=k-t[rch][op].cntR+t[rch][op].cntL,r=mid,o=lch;
}
return l;
}
k = k - stk[i].cntR + stk[i].cntL;
}
assert(0);
return -1;
}
Node merge(const Node& p,const Node& q,int op){
int elim = min(p.cntR, q.cntL);
Node ret{min(p.o,q.o)>>1,p.l,q.r,p.cntL+q.cntL-elim,p.cntR+q.cntR-elim,max(p.ans,q.ans)};
int newans;
if(p.cntR == q.cntL){
newans = (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r)
- (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
}
else if(p.cntR >= q.cntL){
// q 的被消耗完了
newans = (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r)
- (getkth_R(p.o,p.l,p.r,op,q.cntL+1)+1) + 1;
}
else{
// p 的被消耗完了
newans = (getkth_L(q.o,q.l,q.r,op,p.cntR+1)-1)
- (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
}
ret.ans = max(ret.ans, newans);
return ret;
}
void build(int o,int l,int r){
if(l==r){
t[o][0] = {o,l,r, a[l]==1,a[l]==0,0};
t[o][1] = {o,l,r, a[l]==0,a[l]==1,0};
return;
}
int lch=o<<1,rch=o<<1|1;
int mid=(l+r)>>1;
build(lch,l,mid);build(rch,mid+1,r);
t[o][0] = merge(t[lch][0],t[rch][0],0);
t[o][1] = merge(t[lch][1],t[rch][1],1);
}
void modify(int o,int l,int r,int ql,int qr){
if(ql <=l && r<=qr){
inv(o);return;
}
pushdown(o);
int lch=o<<1,rch=o<<1|1;
int mid=(l+r)>>1;
if(ql<=mid)modify(lch,l,mid,ql,qr);
if(qr>mid) modify(rch,mid+1,r,ql,qr);
t[o][0] = merge(t[lch][0],t[rch][0],0);
t[o][1] = merge(t[lch][1],t[rch][1],1);
}
Node query(int o,int l,int r,int ql,int qr){
if(ql<=l && r<=qr)return t[o][0];
pushdown(o);
int lch=o<<1,rch=o<<1|1;
int mid=(l+r)>>1;
if(qr<=mid)return query(lch,l,mid,ql,qr);
if(ql>mid)return query(rch,mid+1,r,ql,qr);
return merge(query(lch,l,mid,ql,qr),query(rch,mid+1,r,ql,qr),0);
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,1,n);
int lastans = 0;
while(m--){
int op,l,r;cin>>op>>l>>r;
l=(l+lastans)%n+1,r=(r+lastans)%n+1;
if(l>r)swap(l,r);
if(op==1){
lastans = query(1,1,n,l,r).ans;
cout << lastans << '\n';
}
else modify(1,1,n,l,r);
}
return 0;
}
```