题解 P6012 【【模板】线段树分裂】

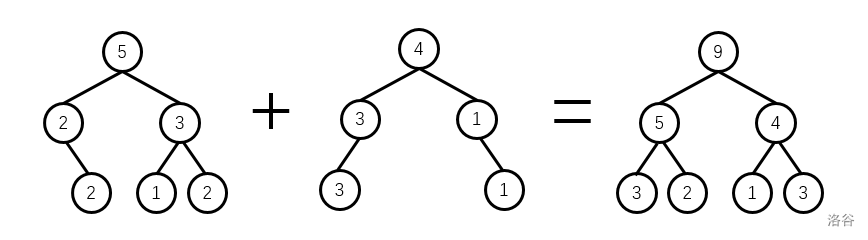
线段树合并&分裂 网上找线段树合并/分裂的博客，讲得很清楚的也不多，某些部分只有自己 yy 一下了。 前置芝士：权值线段树，动态开点线段树。 在以下讨论中，我们设值域都为 $[1,n]$ 中的整数。 先定义代码中的一些东西： $ch[i][0]$ 表示 $i$ 的左子结点，$ch[i][1]$ 表示 $i$ 的右子结点，$val[i]$ 表示 $i$ 点维护的值（出现了多少个该值域中的数） ------ 一、线段树合并 有时我们需要整合两棵权值线段树的信息，这个整合的过程称为线段树合并。我们以最简单的合并为例：将两棵树相加。 两棵树如何相加呢？在权值线段树上，每个点维护了一个当前区间中数的个数，而数的个数是可以相加的，这个合并的过程可以理解为：把两个可重集合并，对应的权值线段树上发生的过程。而相加的原理很简单，两棵同构的线段树，只需要对应位置相加即可，如图：  注意动态开点线段树上某些点是缺的，其值当然是 $0$。 如何合并两棵线段树呢？ 暴力是很简单的，我们枚举 $1$ 到 $n$，将第二棵树中对应位置上的值在第一棵树上做单点修改即可。 这个方法可以用启发式合并进一步优化，但只能适用于一些特殊情况（比如说如果带了分裂或者一个值在多棵树上出现，启发式合并就歇菜了）。 ------ 而我们可以递归处理线段树合并，设我们现在要合并的是以 $x,y$ 为根的两棵子树，要确保它们在线段树上处于同一位置（即它们是两棵树上代表同一区间的点）。 如果 $x,y$ 其中一个为 $0$ （也就是某个权值线段树上没有这个位置的点），无需合并，返回另一个非 $0$ 的点即可。 否则，我们先合并 $x,y$ 的左右子结点，再根据两子结点的信息整合得到 $x,y$ 合并的结果。 线段树合并一般有两种写法：新建结点和不新建结点。但是两者原理是一样的。 新建结点的写法： 新建一个结点 $p$ 作为 $x,y$ 合并的结果。将 $ch[x][0]$ 和 $ch[y][0]$ 的合并结果记为 $sl$，$ch[x][1]$ 和 $ch[y][1]$ 的合并结果记为 $sr$，令 $sl,sr$ 分别为 $p$ 的两个子结点，对 $p$ 做一次 pushup​ 即可得到结果。此后 $x,y$ 就没有用的，可以回收（节省空间的方法）。但是有时 $x,y$ 的信息不能丢，这时就不能回收。 （这里原先的代码有点问题，先删了） 不新建结点的写法： 如果一个点合并完就可以扔掉，那还可以写得更加简便，直接将 $x$ 作为合并后的结果，将 $y$ 的值加到 $x$ 上即可（直接对应位置相加），甚至不需要 pushup，但是注意，如果 $x=0$，返回的是 $y$，所以比较保险的写法是 $x=merge(x,y)$。 事实上这里我们连当前区间的左右端点 $l,r$ 也可以去掉，因为到叶结点后 $ch[x][i]$ 自然是 $0$，自然会返回。 ```cpp int merge (int x,int y) { if (!x||!y) {return x+y;} // 只有一边有点，不用合并 val[x]+=val[y]; // 信息整合 ch[x][0]=merge(ch[x][0],ch[y][0]); ch[x][1]=merge(ch[x][1],ch[y][1]); del(y); // 垃圾回收 return x; } ``` 这东西看着很一般，复杂度怎么样呢？ 单独讨论一次合并的复杂度没有什么意义，如果两棵树都是满的，复杂度就到 $O(n)$ 了，所以一般从均摊角度来讨论。 ------ 如果现在有 $m$ 棵线段树（每棵树初始只有一个位置有权值），经过若干次合并最后变成 $1$ 棵，此过程的复杂度是多少呢？ 例题：[P4556](https://www.luogu.com.cn/problem/P4556)，[P5298](https://www.luogu.com.cn/problem/P5298) 不说具体怎么做了，这些题都有很完整的题解，我就分析一下复杂度（这些题都符合上面提到的模型）。 一开始有 $m$ 棵树，只有一个位置有权值，所以一棵树上结点数量为 $O(\log n)$，$m$ 棵树的结点总数也就是 $O(m\log n)$。 分析上面的代码，发现每一次进入 merge 函数，要么停止递归，要么继续递归并有一个点被垃圾回收。显然停止递归的 merge 次数与继续递归的 merge 次数同阶（不继续递归的情况是从递归的情况出来的，不会超过其两倍的数量）。 因此整个过程的复杂度就等于继续递归的 merge 函数进入次数的复杂度（每一次执行 merge 在不考虑递归时复杂度 $O(1)$），也就等同于被删除的结点个数，是不超过 $O(m\log n)$ 的（有点像势能分析？）。 注意复杂度本身和是否回收结点没有关系，只是借以分析而已。 所以整个过程的复杂度也就是 $O(m\log n)$。 但是线段树合并的复杂度不总是对的，不过本题中 $1$ 操作的复杂度我不知道是否是均摊 $\log n$ 的，希望有人能证明/证伪一下。 ------ 二、线段树分裂 将一个可重集前 $k$ 小的数与之后的数分成两个集合，那么对应的权值线段树就要裂成两棵权值线段树。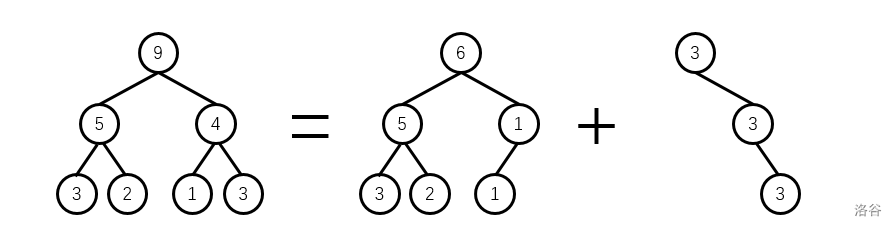 举个栗子：将 $[1,3]$ 和 $[4,4]$ 分开（这里为了方便直接用权值描述了，一般是按照第 $k$ 小的位置来的）：  暴力当然也很简单，找到第 $k$，后面的值新建一棵树，在原树上减掉即可。 然而我们可以仿照 FHQ Treap 的套路，实现 $O(\log n)$ 的分裂。 设我们现在要将以 $x$ 为根的树分裂成 $x,y$ 为根的这两棵树（$y$ 本来是不存在的，传引用），以第 $k$ 小为界，前 $k$ 小在 $x$，之后的在 $y$。 首先看 $x$ 的左子树的值 $v$，如果 $v<k$，那么左侧依然归 $x$（不需要处理），递归右侧即可，注意 $k$ 变成了 $k-v$。 如果 $v=k$，那么左边归 $x$，右边归 $y$ 即可。 如果 $v>k$，那么右边归 $y$，递归左侧即可。 看完结构后看权值，$x$ 的新权值当然是 $k$，那么 $y$ 的权值也就是 $x$ 原先的权值减去 $k$ 了。 可以发现，如果 $v\ge k$，那么 $y$ 的右子结点都是需要赋值的，下面的代码直接归到了同一句里（else 所在的那一句）： ```cpp void split (int x,int &y,ll k) { y=newnod(); ll v=val[ch[x][0]]; if (k>v) {split(ch[x][1],ch[y][1],k-v);} else {swap(ch[x][1],ch[y][1]);} // 右子树归 y，x 的右子树变成 0 if (k<v) {split(ch[x][0],ch[y][0],k);} val[y]=val[x]-k; val[x]=k; return; } ``` 这个每次只递归一边，复杂度是 $O(\log n)$ 没啥问题。 ------ 三、这道题 每个操作分别来看。 将 $[x,y]$ 分裂出来：先分出 $[1,x-1]$，再从 $[x,n]$ 中分出 $[x,y]$ 和 $[y+1,n]$，最后把 $[1,x-1]$ 和 $[y+1,n]$ 合并。我注意到 std 不是这样的，std 的分裂写的就是分裂出一个区间，我在这里用了一次合并，但是复杂度是对的，稍后会证明复杂度为 $O(\log n)$； 将 $t$ 树合并入 $p$ 树：单次合并即可，不确定复杂度，但是不超过 $2\times 10^3$ 次总没问题的； $p$ 树中插入 $a$ 个 $q$：单点修改，复杂度 $O(\log n)$； 查询 $[x,y]$ 中数的个数：区间求和，复杂度 $O(\log n)$； 查询第 $k$ 小：经典操作，复杂度 $O(\log n)$。 最后说一下 $0$ 操作的复杂度： 两次分裂是 $O(\log n)$ 没问题，主要看合并。注意合并的两个区间没有交集，我们就看一看每一层会涉及几个点。 对于第 $1$ 层：总共就 $1$ 个点... 对于第 $i$ 层：如果第 $i-1$ 层只递归下来 $1$ 个点（设为 $u$），再设 $x$ 和 $y$ 为 $u$ 的左右子结点。如果前一棵树占了 $x,y$ 两个点，那么因为后一棵树占的区间严格在前一棵树之后，所以只会占 $y$，那么需要递归的只有 $y$，反过来的话同理需要递归的只有 $x$，所以第 $i$ 层也只需要递归 $1$ 个点。 每一层只往下递归一个点，复杂度就是 $O(\log n)$ 了。 代码： ```cpp #include <bits/stdc++.h> #define ll long long using namespace std; const int MAXN=200010; int n,m,tot,cnt,seq=1,op,x,y,z,bac[MAXN<<5],ch[MAXN<<5][2],rt[MAXN]; ll val[MAXN<<5]; int newnod () {return (cnt?bac[cnt--]:++tot);} void del (int p) { bac[++cnt]=p,ch[p][0]=ch[p][1]=val[p]=0; return; } void modify (int &p,int l,int r,int pos,int v) { if (!p) {p=newnod();} val[p]+=v; if (l==r) {return;} int mid=(l+r)>>1; if (pos<=mid) {modify(ch[p][0],l,mid,pos,v);} else {modify(ch[p][1],mid+1,r,pos,v);} return; } ll query (int p,int l,int r,int xl,int xr) { if (xr<l||r<xl) {return 0;} if (xl<=l&&r<=xr) {return val[p];} int mid=(l+r)>>1; return query(ch[p][0],l,mid,xl,xr)+query(ch[p][1],mid+1,r,xl,xr); } int kth (int p,int l,int r,int k) { if (l==r) {return l;} int mid=(l+r)>>1; if (val[ch[p][0]]>=k) {return kth(ch[p][0],l,mid,k);} else {return kth(ch[p][1],mid+1,r,k-val[ch[p][0]]);} } int merge (int x,int y) { if (!x||!y) {return x+y;} val[x]+=val[y]; ch[x][0]=merge(ch[x][0],ch[y][0]); ch[x][1]=merge(ch[x][1],ch[y][1]); del(y); return x; } void split (int x,int &y,ll k) { if (x==0) {return;} y=newnod(); ll v=val[ch[x][0]]; if (k>v) {split(ch[x][1],ch[y][1],k-v);} else {swap(ch[x][1],ch[y][1]);} if (k<v) {split(ch[x][0],ch[y][0],k);} val[y]=val[x]-k; val[x]=k; return; } int main () { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) { scanf("%d",&x); modify(rt[1],1,n,i,x); } for (int i=1;i<=m;i++) { scanf("%d",&op); if (op==0) { scanf("%d%d%d",&x,&y,&z); ll k1=query(rt[x],1,n,1,z),k2=query(rt[x],1,n,y,z); int tmp=0; split(rt[x],rt[++seq],k1-k2); split(rt[seq],tmp,k2); rt[x]=merge(rt[x],tmp); } else if (op==1) { scanf("%d%d",&x,&y); rt[x]=merge(rt[x],rt[y]); } else if (op==2) { scanf("%d%d%d",&x,&y,&z); modify(rt[x],1,n,z,y); } else if (op==3) { scanf("%d%d%d",&x,&y,&z); printf("%lld\n",query(rt[x],1,n,y,z)); } else if (op==4) { scanf("%d%d",&x,&y); if (val[rt[x]]<y) {printf("-1\n");continue;} printf("%d\n",kth(rt[x],1,n,y)); } } return 0; } ```