P6219
Feyn
·
·
题解
双倍经验,一模一样
说一下模拟赛场上和场下关于这道题的心路历程。
然后我就开始思考能不能把这玩意拆分成几个部分,一顿手玩之后发现一种妙的图,具体构造方法是三个点为一列,列和列之间完全连边,不相邻的列不连边。大概长这样:
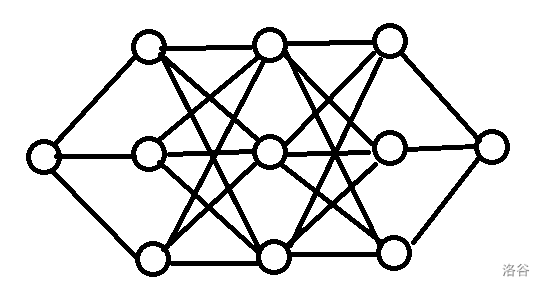
发现这种图有一个性质,随着列数越来越多,整体的答案会是 $1\ -2\ \ 4\ -8\dots$ 这样的,十分有规律。而我们知道这个图形有一个性质,即各部分的贡献可以累加。于是就可以把询问的数拆分成许多数之和,然后就对各部分进行处理即可。于是考场上得了 $48$ 分,代码就不放了。
场下看了别人的代码并结合了官方的题解,却仍然久久未能明白,特别是那句 we
can add two nodes to a new level that are connected to all from the previous level 中的 previous 具体指什么百思不得其解(我太弱了),在咨询其它大佬之后用我的语言给出这道题的完整解法:
其实考场上的代码已经很靠近正解了,只是没有把问题进行很好的具象分析。我们可以令 $f_{x,0/1}$ 代表序列最后一个节点是 $x$,并且序列长度奇偶性确定时的方案数,转移就是枚举所有能到达 $x$ 的 $y$,$f_{x,p}=\sum f_{y,1-p}$。然后发现没必要加上后面那一维,所以我们可以令 $g_x$ 是 $f_{x,1}$ 和 $f_{x,0}$ 的差,那么方程就变成了 $g_x=-\sum g_y$。
观察上面那个模型,发现任意一个点都可以被前面任意一层的任意节点到达,所以可以记 $sum_x$ 为前 $x$ 层 $g$ 值总和,那么第 $x+1$ 层的 $g$ 值应该是 $-sum_x$,更新一下就有 $sum_{x+1}=sum_x-sum_x\times q=(1-q)sum_x$(假设每层的节点个数是 $q$)。有两个特殊值:$q=3$ 时会让总和扩大一倍,而 $q=2$ 时会让总和取反,我们可以利用这两个操作来构造出输入值。
显然越靠前的位置对答案的影响越大,考虑特殊情况,即 $K=2^r$ 的情况,显然我们可以一开始用一个 $q=3$ 的层,然后一直用 $r$ 次,这样可以保证得到的结果绝对值一定是 $K$,如果正负不对的话直接用 $q=2$ 的做法取反即可。
然后思考如何推广上述流程,也就是如何在一个二进制位上放一。通过第一个 subtask 的经验,任意一个直接和起点相连的边都对答案有一个负的贡献,那么假如当前的总和是负的,那么我们在本层添加一个直接和 $1$ 相连的点就可以了;如果总和是负的,那么直接通过操作把总和取反之后就是前面的问题了。
其它的就没什么了,有些细节需要自己思考一下,但如果理解了那些问题就很简单了。
代码比较短,由于某些原因压了点行,不影响可读性。
```cpp
#include<bits/stdc++.h>
//#define feyn
#define int long long
#define adding for(int x:last)for(int y:now)ans.push_back((node){x,y})
using namespace std;
inline void read(int &wh){
wh=0;char w=getchar();int f=1;
while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar();}
wh*=f;return;
}
int m,cnt=1;
struct node{int a,b;};
vector<int>endll,last,now;
vector<node>ans;
signed main(){
#ifdef feyn
freopen("in.txt","r",stdin);
#endif
read(m);
if(m==0){printf("3 2\n1 2\n 2 3\n");return 0;}
if(m==1){printf("1 0\n");return 0;}
if(m==-1){printf("2 1\n1 2\n");return 0;}
bool neg=false,op=false;if(m<0)m=-m,neg=true;
int lg=1;while((1ll<<lg)<=m)lg++;lg--;
for(int i=lg-1;i>=0;i--){
now.clear();for(int j=0;j<3;j++)now.push_back(++cnt);
if(i==lg-1)for(int x:now)ans.push_back((node){1,x});else adding;
if(((1ll<<i)&m)==0){last=now;op^=1;continue;}
if(op){last=now;now.clear();for(int j=0;j<2;j++)now.push_back(++cnt);adding;}
now.push_back(++cnt);ans.push_back((node){1,cnt});last=now;op=true;
}
if(neg==op){now.clear();for(int i=0;i<2;i++)now.push_back(++cnt);adding;}
++cnt;for(int x:now)ans.push_back((node){x,cnt});
printf("%lld %lld\n",cnt,ans.size());
for(node x:ans)printf("%lld %lld\n",x.a,x.b);
return 0;
}
```