题解 P5658 【括号树【民间数据】】
Gu_Pigeon
·
·
题解
决定 \Huge\text{AFO} 前写篇题解,讲讲考场上的过程吧,也就当写游记吧 (游什么)。
$\text{2019-11-16 09:xx}$ 打了四十几分钟才肝完T1,~~唉我真没有实力~~(~~还没开 `ull` 结果95~~)
在草稿纸上画了两笔手玩样例以后,对T2大概有点理解了。
最暴力的,枚举每一个节点( $O(n)$ ),再枚举每一个子区间( $O(n^2)$ ),再判断是否合法( $O(n)$ ),时间复杂度 $O(n^4)
接下来考虑优化。
发现:
- 一个节点到1号节点(根节点)之间的括号序列合法子串数,等于其父节点到1号节点(根节点)之间的括号序列合法子串数,加上以该节点为结尾的合法子串数
$RT$(如图):
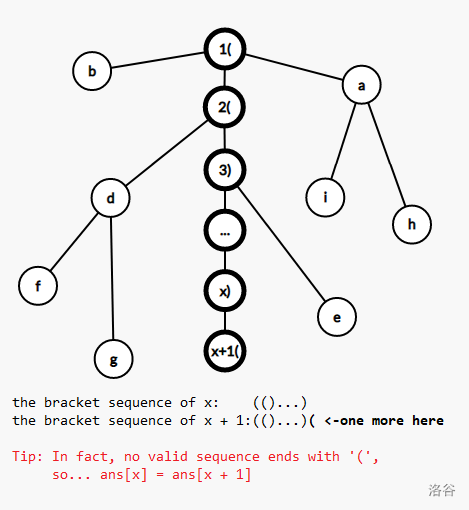
那么,有一种想法,就是dfs整棵树,将父节点的答案下传到子节点,然后判断以最后一个括号为结尾的合法括号序列有多少就可以了。
朴素判断序列是否合法,即 $O(n)$ 枚举以最后一个括号为结尾的序列,$O(n)$ 判断,复杂度$O(n^3)$,少了个n。
~~当然你可以判断最后一位是 `(` 的情况就跳过枚举直接转到下一层~~
$\text{2019-11-16 09:3x}$ 现在还有一个问题,判断括号序列实在是**太 慢 了**
然后就想起一种 基 本 操 作,用栈模拟括号序列
> `(` 表示将栈中的 `size++`
> `)` 表示将栈中的 `size--`
2. 符合的括号序列,需要size的值一直为非负数且开始的size与结束的size相等
$ prove $: 当一个括号序列为合法的,当且仅当:
> * `(` 的个数 = `)` 的个数
>
> * 对于每一个位置,前缀`(`的个数不少于`)`的个数
那么实际上我们不需要一个真正的栈而只需要记录size值即可
那么如何判断子串是否合法?毕竟子串的开头size不一定为零
举栗:
```
bracket sequence: ( ( ) ( ( ) ) ( ( ) ) ) ) ( ) ( (
value of size: 1 2 1 2 3 2 1 2 3 2 1 0 -1 0 -1 0 1
```
附上方样例折线图:
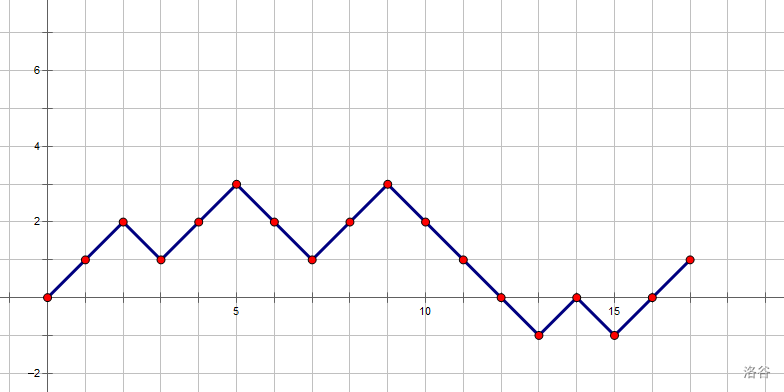
为保证子串为合法序列,根据上方~~照猫画葫芦~~可得合法条件为:
> * 子串头的size值 = 子串尾的size值
>
> * 在子串中所有位置的size值都大于等于子串尾的size
在图形上直观的表示就是:在一段范围内形成“山峰”
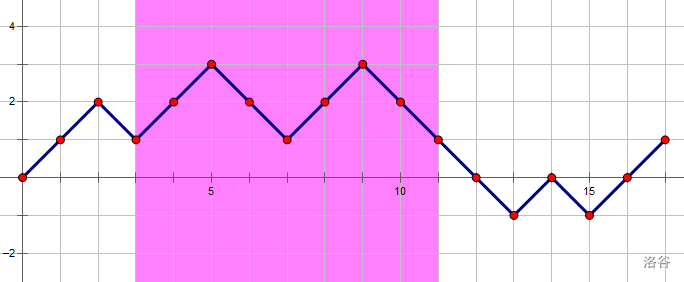
上图中颜色覆盖部分是合法的,因为这段区间两端的值相等且中间点的高度都不小于两端
$\text{2019-11-16 10:xx}$ 所以可以想到,对于每一个右端点固定的询问,在一段符合的区间内找到与右端点值相等的点的个数,**符合**的区间指区间内的所有点的高度不小于右端点高度,例如:
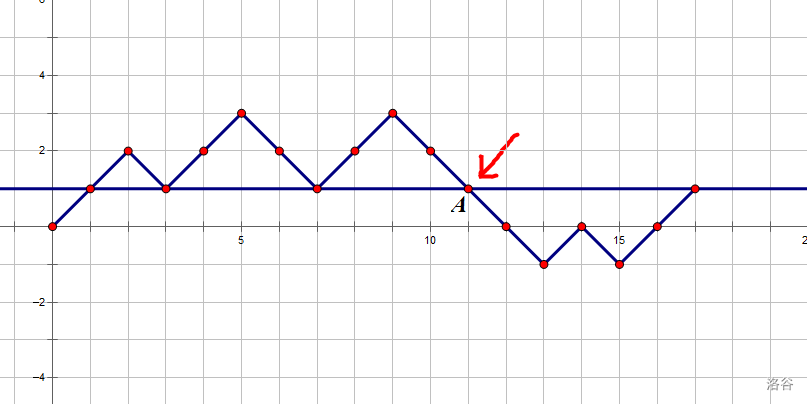
求以点A结尾的合法区间个数时,发现在x坐标为1的点至A点之间的点都是不低于A点的,所以左端点的取值可以在 `[1, A - 1]` 之间,而在合法区间内有3个高度与A相等的点,事实上这些点都可以作为左端点,所以以A为右端点的合法括号序列子串有3个。
计算出各个高度后,我们在$O(n)$时间内计算出了合法子串数。
$\text{2019-11-16 10:2x}$ 需要注意:
* 左端点的合法区间的左边界需要保证区间内的点的高度**全部**都要大于等于右端点,所以发现第一个小于右端点的,则马上停止。
现在,时间复杂度$O(n^2)$,考虑继续优化。
两种选择:
1. 数据结构优化
2. 省去冗余数据
用数据结构处理的话,需要考虑在尽量短的时间内求出**一段区间内**某一个**值**出现的个数
## 主席树是你的最佳选择!
~~什么?不会?~~
## 树状数组现身!
毕竟以往的NOIP中(~~虽然现在是CSP~~)有很多毒瘤数据结构题(比如列队?)都可以用树状数组来做,不如就往这方面想一想。
$\text{2019-11-16 10:3x}$ 树状数组不会MLE吗?
~~当然会了~~
如果直接用树状数组代行主席树的功能的话当然会MLE,所以考虑简化记录下来的数据。
然后发现,要找的区间其实是有一定规律的,就是在 `(目前最后一个x-1的位置, 目前位置)` 其中找出 `x` 的个数(其中 `x` 指的是目前位置的`size`值,注意是**全开区间**)
那么其实我们只需要记下**最近一次**`x-1`出现的位置,再维护一下前缀和是不是就可以了呢?
~~似乎没有那么简单~~
> Q:这玩意用树状数组咋维护啊?
>
> A:树状数组维护前缀和,再加一个以值域为下标的数组,记录最近的`x-1`出现在哪里就可以了。
>
> Q:但是这还是要用值域中各个值出现次数前缀和的树状数组,还是会MLE吧?
>
> A:~~对啊~~
>
> Q:但是这前缀和**直接用数组记下来**不就好了吗!
>
> A:~~emmm你说的都对~~
$\text{2019-11-16 10:5x}$ 经过一定的推导,我们发现只需要记下当前值为 `x-1` 时前面已经有几个值为 `x` 的点,并在找到一个值为 `x` 的点时,先将answer加上 `目前 x 的出现次数(不包括该点)-先前求出的x-1前的x个数`,那么我们就在 $O(1)$时间内完成了一次答案的统计!
$\text{2019-11-16 11:00}$ 再梳理一下,我们就得出了统计的流程:
```
dfs の 过程:
开始
求出当前size值;
让cnt[当前size值]等于precnt[当前size值 + 1];
precnt加上1
统计该节点答案 = precnt[x] - cnt[x-1]
对于该节点的所有儿子 dfs(儿子);
回溯
结束
```
`cnt[x-1]` 表示最近的 `x-1` 的前面 `x` 的个数。
`precnt[x]` 表示 `x` 出现的个数
这部分的代码写出来如下:
```
void dfs(int x, long long res, int sum)
{
int tt = res, tmp;
sum += a[x];
tmp = cnt[sum + N];
if (~a[x]) cnt[sum + N] = precnt[sum + N]; else tt += precnt[sum + N] - cnt[sum + N];
++precnt[sum + N];
for (int i = head[x]; i; i = nxt[i])
{
int y = to[i];
dfs(y, tt, sum);
}
ans ^= (long long)x * tt;
cnt[sum + N] = tmp;
--precnt[sum + N];
}
```
你可能会发现这里的实现有一些不同:
```
if (~a[x]) cnt[sum + N] = precnt[sum + N]; else tt += precnt[sum + N] - cnt[sum + N];
```
这一句中,因为 `a[x]` 要么是 `1` ,要么是 `-1` 。
当 `a[x] == 1` 时,说明当前的值 `x` 是由 `x-1` 加一得来的,所以要改变 `cnt` 的值,而当一个序列以 `(` 结尾(即 `a[x] == 1`)时,很明显这个括号是不会有贡献的;
当 `a[x] == -1` 时,说明当前的值 `x` 是由 `x+1` 减去一得来的,所以要统计新增加的答案,而不去更新 `cnt`;
这样,基本上这题就解决了,**注意:`cnt` 数组和 `precnt` 数组是以值域为下标的,而会出现负数所以上面的数组下标在使用时要 `+N`**
$\text{2019-11-16 11:10}$ 然后就有了下面的代码:
```
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int to[N], nxt[N], head[N], tot, cnt[N << 1], precnt[N << 1], a[N], n, x;
long long ans;
char s[N];
inline void addedge(int x, int y)
{
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
void dfs(int x, long long res, int sum)
{
int tt = res, tmp;
sum += a[x];
tmp = cnt[sum + N];
if (~a[x]) cnt[sum + N] = precnt[sum + N]; else tt += precnt[sum + N] - cnt[sum + N];
++precnt[sum + N];
for (int i = head[x]; i; i = nxt[i])
{
int y = to[i];
dfs(y, tt, sum);
}
ans ^= (long long)x * tt;
cnt[sum + N] = tmp;
--precnt[sum + N];
}
int main()
{
scanf("%d%s", &n, s);
for (int i = 0; i < n; i++)
if (s[i] == '(') a[i + 1] = 1; else a[i + 1] = -1;
for (int i = 2; i <= n; i++)
scanf("%d", &x), addedge(x, i);
++precnt[N];
dfs(1, 0, 0);
printf("%lld", ans);
}
```
~~然后就只剩下写T3暴力的时间了~~
~~虽然也就只会暴力~~
最后 Day1 205分,还行吧~~虽然人均210~~
~~Day2 爆炸,我$\Huge\text{AFO}$了~~