P8727 [蓝桥杯 2020 国 A] 填空问题 题解
wuhan1234
·
2023-04-08 12:13:24
·
题解
A 合数个数
直接用循环进行枚举搜索。编写的函数如下。
void work1()
{
int ans=0;
for (int i=4;i<=2020;i++)
{
int j;
for (j=2;j*j<=i;j++)
if (i%j==0) break;
if (j*j<=i) ans++;
}
printf("%d\n", ans);
}
执行上面的处理函数,输出结果为:1713 。
B 含 2 天数
直接用循环对每一天进行枚举判断,若年、月、日数字中含有 2 ,则计数。
编写的函数如下。
int check(int x) // 判断整数x 中是否含有数字 2
{
while(x)
{
if (x%10==2) return 1;
x/=10;
}
return 0;
}
void work2()
{
int month[2][13]={{0,31,28,31,30,31,30,31,31,30,31,30,31},
{0,31,29,31,30,31,30,31,31,30,31,30,31}};
int y,m,d,ans=0;
for (y=1900;y<=9999;y++)
{
int f;
if (y%400==0||(y%4==0 && y%100!=0)) f=1;
else f=0;
for (m=1;m<=12;m++)
{
for (d=1;d<=month[f][m];d++)
{
if (check(y)||check(m)||check(d)) ans++;
}
}
}
printf("%d\n", ans);
}
执行上面的处理函数,输出结果为:1994240 。
C 本质上升序列
用线性动态规划进行求解。
定义状态 dp_i 表示以字符 s_i 结尾的本质不同的方案数。
由于第 i 个字符的状态只会和前 i-1 个字符有关,因此我们需要枚举前 i-1 个字符。
当前 i-1 个字符中有某个字符 s_j 和 s_i 相同时,那么就会出现重复的方案;但是由于 dp_i 是一定已经包含了 dp_j 的,所以为了避免重复,可以令 dp_j=0 。
当前 i-1 个字符中有某个字符 s_j 小于 s_i 时,那么 dp_i=dp_i+dp_j 。因为 s_i>s_j ,所以直接在以 s_j 结尾的本质上升序列结尾加一个字符 s_i ,这样也是一个本质上升序列。这样可以继承 dp_j 的所有可行方案。
当前 i-1 个字符中有某个字符 s_j 大于 s_i 时,直接跳过即可。
最后结果便是 dp_1+dp_2+…+dp_{200} 。
编写的函数如下。
void work3()
{
int dp[210]={0};
char s[210]="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhewl";
int ans = 0;
int i,j;
for (i=0;i<strlen(s);i++)
{
dp[i]=1;
for (j=0;j<i;j++)
{
if (s[i]==s[j]) dp[i]=0;
else if (s[j]<s[i]) dp[i]+=dp[j];
}
}
for (i=0;i<strlen(s);i++) ans+=dp[i];
printf("%d\n", ans);
}
执行上面的处理函数,输出结果为:3616159 。
D 咫尺天涯
一个 k 阶的皮亚诺曲线有 3^k 行,每行 3^k 列,共 3^k\times 3^k 个格子,在这些格子中,每行中相邻的格子数有 3^k-1 个,每列中相邻的格子数也有 3^k-1 个,因此相邻的格子总数为 2\times 3^k \times (3^k-1) 个。
例如,1 阶皮亚诺曲线中相邻的格子有 2\times 3 \times (3-1)=12 个。
由题目给出的示意图可知,一个 $k$ 阶的皮亚诺曲线可以划分为 $9$ 个 $k-1$ 阶的皮亚诺曲线,而每个 $k-1$ 阶曲线内部相邻两个格子的距离和不受其余同阶曲线的影响。
设一个 $k-1$ 阶皮亚诺曲线内部相邻两个格子的距离和为 $a$,每两个 $k-1$ 阶皮亚诺曲线间上下相邻的格子的距离和为 $b$,每两个 $k-1$ 阶皮亚诺曲线间左右相邻的格子的距离和为 $c$,则一个 $k$ 阶皮亚诺曲线内部相邻两个格子的距离和为 $9\times a+b+c$。
例如,对于 $2$ 阶皮亚诺曲线中相邻的格子有 $144$ 个,若将 $2$ 阶皮亚诺曲线看成由 $9$ 个 $1$ 阶皮亚诺曲线组成,则每个 $1$ 阶皮亚诺曲线内部相邻的格子有 $12$ 个,两个 $1$ 阶皮亚诺曲线的水平方向上相邻的格子有两行,每行 $9$ 个格子,垂直方向上相邻的格子有两列,每列同样 $9$ 个格子。如下图所示。也就是 $2$ 阶皮亚诺曲线中相邻的 $144$ 个格子可以分解为 $9\times 12 +2\times 9 +2\times 9$。
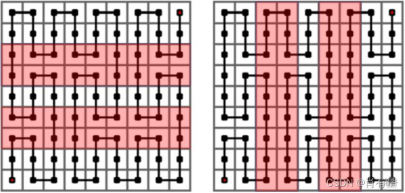
因此,可以从低阶的距离和递推计算出高阶的距离和。其中关键是求低阶曲线之间水平和垂直相邻的距离和 $b$ 和 $c$。
由图可发现,两行或两列之间相邻块的距离和是相等的,于是只需讨论一行或一列的距离和的计算方法,将其和乘以 $2$ 即可。
若将 $k$ 阶的皮亚诺曲线的最左下角的格子设置为原点 $(0,0)$,水平向右为 Y 轴,垂直向上为 X 轴,则每个格子的坐标就确定了。
$k$ 阶的皮亚诺曲线有 $3^k$ 行格子,$k-1$ 阶的皮亚诺曲线有 $3^{k-1}$ 行格子,因此水平方向上,$x$ 值为 $3^{k-1}$ 和 $3^{k-1}-1$ 的格子上下相邻,其 $y$ 值从 $0 \sim 3^k$。
对于相邻的两个格子 $(x,y)$ 和 $(x-1,y)$ 计算出它们与原点的距离,则差的绝对值就是相邻两个格子的距离。
求一个格子 $(x,y)$ 与原点 $(0,0)$ 之间的距离采用递归完成,可参看程序代码。
编写的函数如下。
```c
long long p[14];
long long abs(long long a)
{
return a > 0 ? a : -a;
}
long long calc(int k, long long x, long long y) //求k阶曲线中(x,y)与原点(0.0)的距离
{
if (k == 0) return 0;
long long offset = x / p[k] * 3;
int flag = (offset == 3);
offset += flag ? (3 - y / p[k] - 1) : (y / p[k]);
if ((offset & 1) == 1)
x = p[k] - x % p[k] - 1;
if (flag )
return ((offset + 1) * p[k] * p[k] - calc(k - 1, x % p[k], y % p[k]) - 1) ;
else
return (offset * p[k] * p[k] + calc(k - 1, x % p[k], y % p[k])) ;
}
void work4()
{
int i,j;
p[1]=1;
for (i = 2; i <= 13; i++)
p[i] = p[i-1] * 3;
long long ans=0;
for (i = 1; i <= 12; i++)
{
long long tmp = 0;
for (j = 0; j < p[i + 1]; j++)
{
tmp += abs(calc(i, j, p[i]) - calc(i, j, p[i] - 1));
tmp += abs(calc(i, p[i], j) - calc(i, p[i] - 1, j));
}
ans = 9 * ans + 2 * tmp;
}
printf("%lld", ans);
}
```
执行上面的处理函数,输出结果为:$184731576397539360$。
## E 玩具蛇
从 $16$ 个方格中的每个方格作为起点,分别用 DFS 进行搜索,若从某个起点出发能走 $16$ 步,则就是一种可行的方案。
```c
int dx[4]={1, -1, 0, 0};
int dy[4]={0, 0, 1, -1};
int ans=0;
int vis[16];
int len;
void dfs(int n)
{
if (len == 16)
{
ans++;
return;
}
for (int i = 0; i < 4; i++)
{
int nx = n / 4 + dx[i];
int ny = n % 4 + dy[i];
if (nx < 0 || nx >= 4 || ny < 0 || ny >= 4)
continue;
int next = 4 * nx + ny;
if (!vis[next])
{
vis[next] = 1;
len++;
dfs(next);
vis[next] = 0;
len--;
}
}
}
void work5()
{
for (int i = 0; i < 16; i++)
{
vis[i] = 1;
len++;
dfs(i);
vis[i] = 0;
len--;
}
printf("%d\n", ans);
}
```
执行上面的处理函数,输出结果为:$552$。
有了上面的处理结果,提交给本题的源程序如下。
```c
#include <stdio.h>
#include <string.h>
int main()
{
char T;
scanf("%c",&T);
if (T=='A') printf("1713\n");
else if (T=='B') printf("1994240\n");
else if (T=='C') printf("3616159\n");
else if (T=='D') printf("184731576397539360\n");
else if (T=='E') printf("552\n");
return 0;
}
```