可持久化线段树 / 主席树
Grace2022
·
·
算法·理论
初学者对该类数据结构的评价：思维难度：5；代码难度：5；应用难度：+\infty；调试难度：未知。
本文的每一个知识点都遵循“原理-实现-相关题目/拓展”的顺序讲解，不提供完整代码。若按照目录从前往后阅读本文，并独立写出完整代码，您将学会可持久化线段树的模板和较为基础的应用。较为进阶和困难的应用不被包含在本文。
在学习该数据结构前，您需要会写普通线段树和线段树的动态开点。
可持久化数组
你需要维护这样的一个长度为 n 的数组 a，支持如下两种操作：
- 在版本 v 的基础上，将 a_p 修改为 c。
- 输出版本 v 中 a_p 的值。
此外，m 次操作中的每一次操作，就会生成一个新的版本。版本编号即为当前操作的编号（从 1 开始编号，版本 0 表示初始状态数组）。
对于操作 2，即为生成一个完全一样的版本，不作任何改动。即，询问生成的版本是询问所访问的那个版本的复制。
---
一个比较自然的暴力做法，是定义一个数组 $b_{i, j}$ 表示版本 $i$ 下标为 $j$ 的 $a$ 数组的值，虽然时间是 $O(1)$ 的，但是空间是 $O(nm)$ 的，显然超出空间限制。
可以发现每一个版本实际上只修改一个值，完全没有必要把整个数组都复制下来。
我们依照版本与数组的映射关系建一棵版本树，以版本编号为对应版本树的根节点：
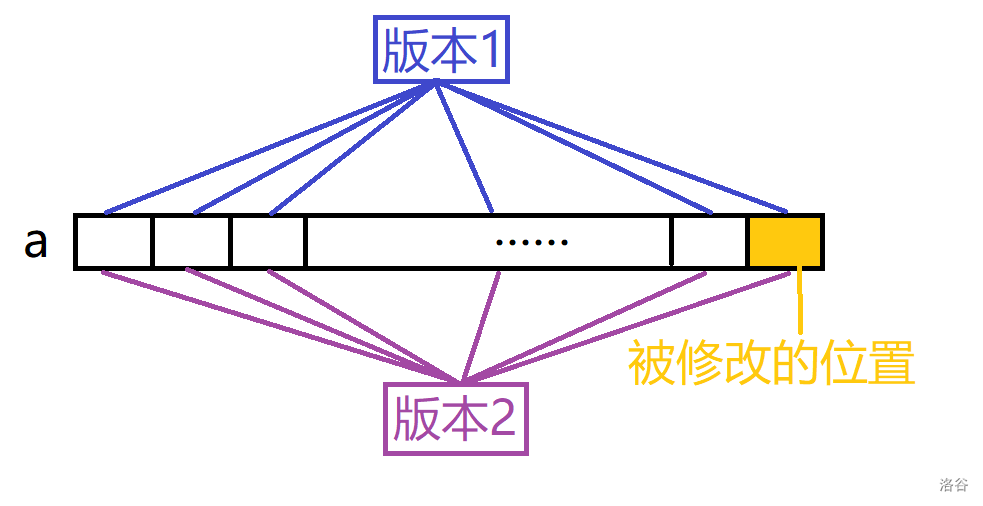
我们希望对所有没被修改的节点建立一个父亲节点，这样“版本 2”只用连两次边了：
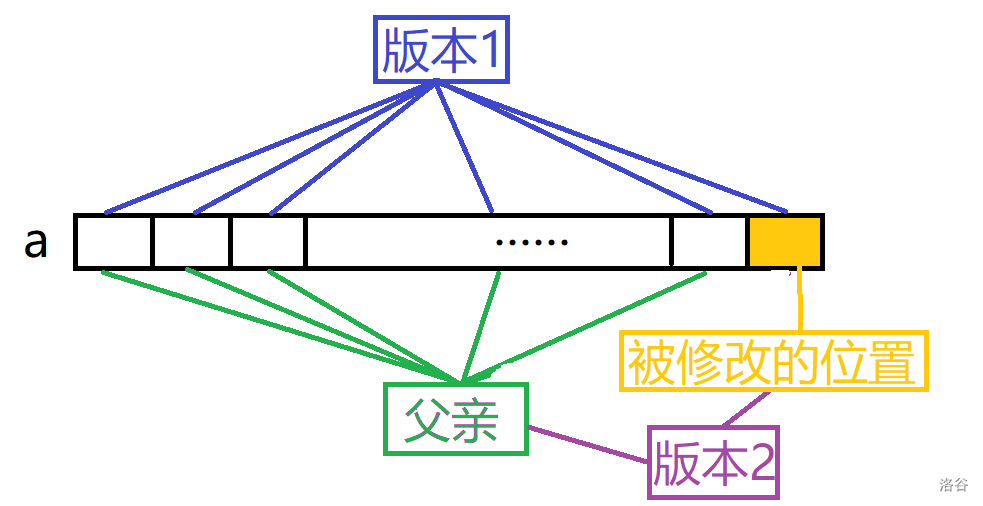
这样的区间连边难以 $O(1)$ 实现，但是可以通过线段树 $O(\log n)$ 实现！
区间连没有修改的位置，相当于在原版本的基础上新建与修改位置相关的节点。
画出线段树就是：
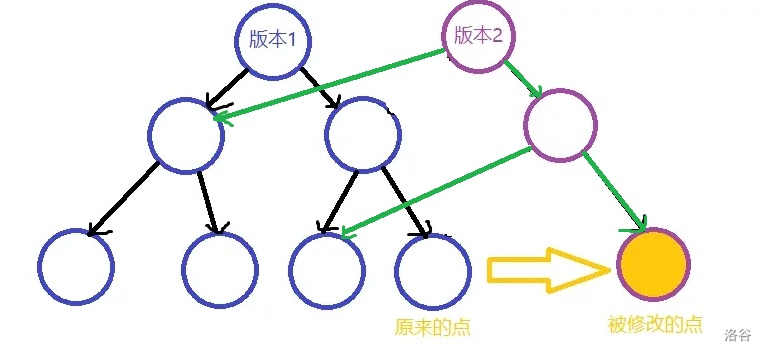
如果要访问版本 1，就从版本 1 的根往下递归，单点查询；如果要访问版本 2，同理，此时的线段树相当于这样：
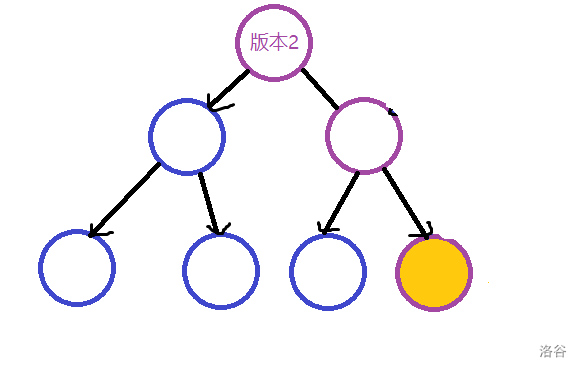
至此，我们就完成了可持久化数组的两个操作。时空复杂度都大概是 $O(n \log n + m \log n)$。
---
由于这里会新建节点，左右儿子指向不同的节点，所以不能用堆式存储法 $rt \times 2$ 和 $rt \times 2 + 1$ 存左右儿子，而应该动态开点。设线段树总节点数为 $cntd$，每个节点信息为 $ls$、$rs$、$val$ 分别表示节点的左右儿子和权值，其中只有叶子节点 $val$ 才有值。
设版本 $i$ 的根节点为 $root_i$，我们要在版本 $v$ 的基础上修改 $a_p$ 为 $c$ 成为版本 $i$。
首先构建初始状态：```Build(root[0], 1, n);```。
需要构建一棵完整的线段树（对应图中的版本 1），包括每个节点左右儿子和叶子节点对应 $a$ 数组的权值：
```cpp
void Build(int &rt, int l, int r){
rt = ++cntd;
if(l == r){
tree[rt].val = a[l];
return;
}
int mid = l + r >> 1;
Build(tree[rt].ls, l, mid);
Build(tree[rt].rs, mid + 1, r);
}
```
接着是单点修改。按照普通线段树的单点修改流程，当前递归到的根节点 $rt$ 即为与修改位置 $p$ 相关的节点。
首先需要把版本 $v$ 的节点信息复制到版本 $i$ 上：```tree[版本 i 的 rt] = tree[版本 v 的 rt];```，由于这里我写的 ```Update``` 函数传的参就是原版本节点编号、返回值是现版本节点编号，所以有 ```tree[++cntd] = tree[rt]; rt = cntd;```，最后在函数结束前 ```return rt;```。调用：```root[i] = Update(p, c, root[v], 1, n);```
接着往正确方向递归，并修改对应节点信息即可。
```cpp
inline int Clone(int rt){
++cntd;
tree[cntd] = tree[rt];
return cntd;
}
int Update(int L, int C, int rt, int l, int r){
rt = Clone(rt);
if(l == r){
tree[rt].val = C;
return rt;
}
int mid = l + r >> 1;
if(L <= mid) tree[rt].ls = Update(L, C, tree[rt].ls, l, mid);
else tree[rt].rs = Update(L, C, tree[rt].rs, mid + 1, r);
return rt;
}
```
最后是单点查询，与普通线段树代码无异，只需要在调用的时候从对应版本的根开始递归即可：```Query(L, root[i], 1, n)```。
注意线段树数组要开够，如果嫌计算空间麻烦建议至少开到 $2^5 \times n$，即 ```tree[N << 5]```，当然有的题目卡空间、有的题目可能因为多次 Update 开到更大，具体情况具体分析。
---
请完成 [P3919 【模板】可持久化线段树 1（可持久化数组）](https://www.luogu.com.cn/problem/P3919)。
---
可持久化数组还有离线做法，这里简单讲一下。
注意到版本 $i$ 是依托于版本 $v$ 的，以所有版本建立节点，连一条从 $v$ 指向 $i$ 的边，于是就形成了一棵树。从根节点版本 $0$ 开始 dfs，每遍历到一个节点就执行对应操作（该修改修改，该查询那个数组记录当前版本的答案），回溯时还原，最后输出答案数组即可。因为两个毫无关系的版本一定不成父子关系，不会互相影响。
时间复杂度 $O(m)$，空间复杂度 $O(n)$。
这个思想其实有一点[线段树分治](https://www.luogu.com.cn/article/azj9ik2c)的味道了，特别是学习了下一节可持久化并查集离线做法中的可撤销并查集后。感兴趣的读者可以自行学习^^
## 可持久化并查集
给定 $n$ 个集合，第 $i$ 个集合内初始状态下只有一个数，为 $i$。
有 $m$ 次操作。操作分为 $3$ 种：
- `1 a b` 合并 $a,b$ 所在集合；
- `2 k` 回到第 $k$ 次操作（执行三种操作中的任意一种都记为一次操作）之后的状态，保证已经进行过至少 $k$ 次操作（不算本次操作），特别的，若 $k=0$，则表示回到初始状态；
- `3 a b` 询问 $a,b$ 是否属于同一集合，如果是则输出 $1$，否则输出 $0$。
$1\le n\le 10^5$，$1\le m\le 2\times 10^5$，$1 \le a, b \le n$。
---
可持久化并查集其实是可持久化数组的运用。
注意到并查集对 $u, v$ 的合并操作实际上是令 $fa_u = v$，而查询操作也与 $fa$ 数组的值有关。对应到可持久化数组上，$fa$ 数组其实就是待修改的 $a$ 数组。那么查询祖先节点 $\text{find}(u)$ 相当于每次 Query 一下 $fa_u$ 的值，直到 $fa_u = u$。
这里的合并**不能路径压缩**，只能选择按秩合并中的按树高 $dep$ 合并或按子树大小 $sz$ 合并，也**不能随机化合并**。如果不理解，请重新学习并查集的原理与时间复杂度证明，或者看看[这篇题解 by chenxinyang2006](https://www.luogu.com.cn/article/dc4docp3)。
以按子树大小 $sz$ 合并为例，我们线段树节点需要维护两个信息 $fa$ 和 $sz$。可以只建一棵线段树，合并时分别 Update 更新，查询祖先 Query 时打包成一个结构体返回；也可以 $fa$ 和 $sz$ 建两棵线段树分别更新查询。
对于前者，两次更新可能会导致我们一个版本建两次 $\log n$ 个新节点。这是没问题的，空间开大一点即可。当然，你也可以保存一个时间点标记 $las$，在第一次修改前：$las = cntd$，在每次新建节点 ```Clone(rt);``` 前判断 ```rt <= las``` 来判断是否是原版本、是否需要加新点。[这篇题解 by 王鲲鹏](https://www.luogu.com.cn/article/n5thkapl) 专门讲了这个点。
这个东西的实现是需要一定的代码能力与调试能力的。但是，不试试怎么知道你能不能一遍 AC 呢？
---
可持久化并查集仍有离线做法。
与可持久化数组类似，以版本编号为节点，以版本间的依赖关系建边，从版本 0 开始 dfs，进入一个节点就操作，退出一个节点就还原。
这里的还原需要用到**可撤销并查集**。由于 dfs 的过程本质就是一个递归栈，用一个栈存储每一次改变的 $fa$ 和 $sz$。在函数开头存储递归前栈的大小 $bef$，在函数结尾挨个弹出还原，直到栈的大小与 $bef$ 相等：
```cpp
while(can.size() != bef){
int u = can.top().u, v = can.top().v;
can.pop();
fa[u] = u; //我的习惯是将 u 合并到 v 上
sz[v] -= sz[u];
}
```
根据可撤销并查集的原理，显然不能通过路径压缩合并破坏并查集结构，而需要按秩合并。这里我用的按子树大小合并。
---
请完成 [P3402 【模板】可持久化并查集](https://www.luogu.com.cn/problem/P3402)。
---
众所周知，并查集最简单广泛的应用就是连通性相关问题。
而有些题目会问在一些限制条件下，与连通性相关的问题。比如给图中的边赋一个权值 $h$，限制为 $h \le p$ 。
如果题目允许离线，可以直接对边排序，$h$ 的答案在 $h - 1$ 作新的并查集合并即可。
但是如果题目强制在线，我们可以把“版本 $i$”定义为限制 $h \le i$ 下的并查集情况，版本 $i$ 的更新依托于版本 $i - 1$，用可持久化并查集实现即可。
请完成 [P4768 [NOI2018] 归程](https://www.luogu.com.cn/problem/P4768)，注意此题**强制在线**。
~~我都提示到这儿了，你不会还不会做吧？~~
## 可持久化权值线段树
给定 $n$ 个整数构成的序列 $a$，$m$ 次查询，每次查询闭区间 $[L, R]$ 内的第 $k$ 小值。
$1 \leq n,m \leq 2\times 10^5$，$0\le a_i \leq 10^9$，$1 \leq L \leq R \leq n$，$1 \leq k \leq R - L + 1$。
---
该类静态区间求 $k$ 小值的问题，做法有很多：莫队/分块、整体二分、线段树合并、划分树、树状数组、Wavelet Tree……蒟蒻不会，蒟蒻瑟瑟发抖，蒟蒻只会主席树。
回忆区间 $[1, n]$ 的 $k$ 小值怎么求，这是权值线段树的基础应用。以值域为“下标”，统计值为 $a_i$ 在序列里的个数。找到第一个前缀和 $\ge k$ 的线段树叶子节点，其所对应的值就是 $k$ 小值。
区间 $[L, R]$ 的 $k$ 小值是一样的，统计值为 $a_i$ 在 $[L, R]$ 里的个数。后面步骤一样。
注意到“统计值为 $a_i$ 在 $[L, R]$ 里的个数”，相当于求区间求和，由此想到前缀和。我们可以以某种方法，记录下 $[1, L - 1]$ 和 $[1, R]$ 的个数和，然后相减即可。
因为 $[1, i]$ 的个数和是在 $[1, i - 1]$ 的基础上加上 $a_i$ 的贡献，“某种方法”就是可持久化权值线段树。版本 $i$ 表示 $a[1, i]$ 所对应的权值线段树，初始版本 $0$ 是一棵空树。
这样，权值区间 $[l, r]$，数组区间 $[L, R]$，$[1, L - 1]$ 对应的线段树节点为 $u$，$[1, R]$ 对应版的线段树节点为 $v$，所对应的个数 $sum = tree_{v} - tree_{u}$。递归求值即可。
所以，求 $k$ 小值的本质就是，在线段树上找到满足条件的个数和。只不过普通权值线段树的节点区间 $[l, r]$ 所对应的个数是直接存在线段树节点里的，而可持久化权值线段树需要通过前缀和相减计算。
```cpp
int Query(int x, int u, int v, int l, int r){
if(l == r) return p[l];
int mid = l + r >> 1, sum = tree[tree[v].ls].cnt - tree[tree[u].ls].cnt;
if(x <= sum) return Query(x, tree[u].ls, tree[v].ls, l, mid);
else return Query(x - sum, tree[u].rs, tree[v].rs, mid + 1, r);
}
```
可持久化权值线段树是动态开点的，且初始状态是空树。也就是说无需 Build，也可以不离散化，不过要根据题目的条件与时空限制定论。
---
请完成 [P3834 【模板】可持久化线段树 2](https://www.luogu.com.cn/problem/P3834)、[P1533 可怜的狗狗](https://www.luogu.com.cn/problem/P1533)。
树上区间 $k$ 小是一样的。把版本 $i$ 的定义改成从根到节点 $i$ 的节点对应的权值线段树。$sum_{[u, v]} = tree_u + tree_v - tree_{lca(u, v)} - tree_{fa_{lca(u, v)}}$。递归的时候传 4 个根即可。
请完成 [P2633 Count on a tree](https://www.luogu.com.cn/problem/P2633)，此题强制在线。
其实只要是权值线段树能做的，且需要区间权值线段树查询的，都可以用可持久化权值线段树做。这部分题就稍微有点难了，因为需要转化，看出此题需要用可持久化线段树。建议从头思考题目，而不是思考“此题怎么用主席树做”。
请完成 [P3567 [POI 2014] KUR-Couriers](https://www.luogu.com.cn/problem/P3567)、[P4587 [FJOI2016] 神秘数](https://www.luogu.com.cn/problem/P4587)。
::::info[题解：P4587 [FJOI2016] 神秘数]
### 题意
给定长度为 $n$ 的正整数序列 $a$，$m$ 次询问，每次询问包含两个参数 $l,r$，求由 $a[l, r]$ 所组成的可重集合的“最小不能被其子集和表示出来的正整数”。$1\le n,m\le {10}^5$，$\sum a\le {10}^9$。
### 思路
设 $a[l, r]$ 已从小到大排序，$a[1, p - 1]$ 可以表示出 $[1, q]$。当前考虑 $a_p$（$a_p \gt a_{p - 1}$，取等的情况在 $a_{p - 1}$ 考虑）：
- $a_p \le q - 1$，此时 $a_p$ 新表示出 $[a_p + 1, a_p + q]$，$a[1, p]$ 可以表示出 $[1, q + a_p]$。
- $a_p \gt q - 1$，此时 $q-1$ 就是答案。
也就是说，$a_p$ 满足不会产生答案的条件是 $a_{p - 1} \lt a_p \le q - 1$。如果有多个 $a_p$，$q$ 更新为 $q + \sum a_p$。
设 $mx = a_{p - 1}$，$q$ 为上述含义，那么对于 $a[l, r]$ 值域上的值，每次贡献都有 $q \gets q + \sum[mx + 1, q - 1]$，注意这里的区间是 $a[l, r]$ 值域上的区间，加的是区间内 $a$ 值的总和。当没有产生新贡献时，即 $q \gets q + 0$ 时，答案即为 $q + 1$。
根据 $mx$ 的定义，每一轮更新 $mx$，都有 $mx \gets q + 1$，这里的 $q$ 时这一轮更新前的 $q$。而 $q$ 的更新所用到的 $mx$ 也是这一轮更新前的 $mx$。
初始 $mx = 0$，$q = 0$。
初看非常之抽象、难以理解，但仔细想想还是能想明白的。这里给出这部分的代码：
```cpp
int l, r, mx = 0, q = 0, sum;
read(l), read(r);
while(1){
sum = getsum(mx + 1, q + 1, root[r], root[l - 1], 1, V);
if(sum == 0){
write(q + 1); putchar('\n');
break;
}
mx = q + 1;
q += sum;
}
```
计算 $\sum[mx + 1, q - 1]$ 的部分（代码中的 ```getsum()``` 函数）可以用可持久化权值线段树实现。
观察 $q$ 的更新，会发现这相当于值域倍增的过程。所以总时间复杂度 $O(m \times \log ^ 2(\sum a_i) \times \log n)$。
:::success[完整代码]
```cpp
#include<bits/stdc++.h>
using namespace std;
template<typename T> inline void read(T &x){
T s = 0; int st = 1; char c = getchar();
while(c < '0' || c > '9'){(c == '-') && (st = -1); c = getchar();}
while(c >= '0' && c <= '9'){s = (s << 3) +(s << 1) + (c ^ 48); c = getchar();}
x = s * st;
}
template<typename T> inline void write(T x){
if(x <0) x= -x, putchar('-');
if(x > 9) write(x / 10);
putchar(x % 10 + 48);
}
#define LL long long
#define PII pair<int, int>
const int N = 1e5 + 5, V = 1e9;
struct node{
int ls, rs, cnt, sum;
}tree[N << 5];
int cntd;
int a[N], root[N];
int Update(int L, int rt, int l, int r){
++cntd; tree[cntd] = tree[rt]; rt = cntd;
if(l == r){
++tree[rt].cnt;
tree[rt].sum += L;
return rt;
}
int mid = l + r >> 1;
if(L <= mid) tree[rt].ls = Update(L, tree[rt].ls, l, mid);
else tree[rt].rs = Update(L, tree[rt].rs, mid + 1, r);
tree[rt].cnt = tree[tree[rt].ls].cnt + tree[tree[rt].rs].cnt;
tree[rt].sum = tree[tree[rt].ls].sum + tree[tree[rt].rs].sum;
return rt;
}
int Query(int L, int R, int u, int v, int l, int r){
if(u == 0 && v == 0 || u == 0) return 0;
// cerr << L << ' ' <<R << ' ' <<l << ' ' << r << ": " << tree[u].cnt - tree[v].cnt << endl;
if(L <= l && r <= R) return tree[u].cnt - tree[v].cnt;
int mid = l + r >> 1, Ans = 0;
if(L <= mid) Ans += Query(L, R, tree[u].ls, tree[v].ls, l, mid);
if(mid < R) Ans += Query(L, R, tree[u].rs, tree[v].rs, mid + 1, r);
return Ans;
}
int getsum(int L, int R, int u, int v, int l, int r){
// cerr << L << ' ' << R << ": " << l << ' ' << r << ' ' << tree[u].sum - tree[v].sum << ' ' << u << endl;
if(u == 0) return 0;
if(L <= l && r <= R){
return tree[u].sum - tree[v].sum;
}
int mid = l + r >> 1, Ans = 0;
if(L <= mid) Ans += getsum(L, R, tree[u].ls, tree[v].ls, l, mid);
if(mid < R) Ans += getsum(L, R, tree[u].rs, tree[v].rs, mid + 1, r);
return Ans;
}
int main(){
int n, m;
read(n);
for(int i = 1; i <= n; ++i){
read(a[i]);
root[i] = Update(a[i], root[i - 1], 1, V);
}
read(m);
for(int i = 1; i <= m; ++i){
int l, r, mx = 0, q = 0, sum;
read(l), read(r);
while(1){
sum = getsum(mx + 1, q + 1, root[r], root[l - 1], 1, V);
if(sum == 0){
// cerr << sum << endl;
write(q + 1);
putchar('\n');
break;
}
mx = q + 1;
q += sum;
// cerr << " q:" << q << " mx:" <<mx << " sum:" << sum << endl;
}
}
return 0;
}
/*
若a[l, p - 1]已经添加，最大值为 mx, 且可以表示的数为[1, q]
若a[p] <= q + 1, 可以表示的数为[1, q + a[p]], 加入区间[a[p], a[p] + q]
若a[p] > q + 1, q + 1为神秘数
最初p = l - 1, q = 0, mx = 0
a[p]的范围为[mx + 1, q + 1], p为[p + 1, r]. p += 数量，q += sum.
若数量为0则ans = q + 1
*/
```
:::
::::
## 结语
如果说线段树维护的是一维信息，可持久化线段树维护的就是二维可减信息，线段树部分维护第一维，“版本”部分维护第二维。例如部分扫描线、在线二维数点问题就可以通过可持久化线段树解决。
可持久化线段树维护静态平面信息（没有修改只有查询），动态维护需要用到树套树。
学会了可持久化线段树，其它可持久化数据结构就不难了。
希望你学得开心^^