题解 P5684 【[CSPJX2019]非回文串【民间数据】】
旭日临窗
·
·
题解
个人认为这道题和道路拆除P5683比较有思维难度,道路拆除的题解已经写过了,好了现在进入正题。
思路:还是正难则反,非回文串不是太好求,所以我们可以用总的方案数减去回文串的数量不就行了吗?
总方案数很好求就是n!,那回文串的数量怎么求呢?
我们想回文串肯定是对称的,所以每个字母都应该是偶数个,特殊情况下最多只能有一个字母的数量是奇数个,否则就不能组成回文串,直接输出总方案数就行了。
所以我们可以预处理出每个字母出现的个数sum[i]表示,如果有一个字母的数量是奇数,sum[i]--就行了,因为那一个字母必然在中间。
好了,现在还有一个问题,回文串的数量怎么求呢,先来看一张图:
如图,n1表示a出现的数量,以此类推,n26表示z的数量,因为回文串是对称的,所以左边每个字母的数量都是n/2,那问题就变得简单了,现在就相当于是求
**我们想**,数量总共是$n$,方案数是$n!$,那数量是$n/2$,方案数不就应该是$\frac{n}{2} !$吗?
还有一点不要忘了,对于每一种字母,假设是$a$,我们都要从$n$个$a$中选出$\frac{n}{2}$个a放到左边,其余放到右边,发现这不就是**组合数学**吗?
[组合数学不会的可以参考一下,这里只有公式](https://zhidao.baidu.com/question/689879375452903724.html)
那到底是$A$还是$C$呢?
我们想左边动,右边也跟着动,但是**每个字母可以对应同类的其余字母**,什么意思呢,见图:
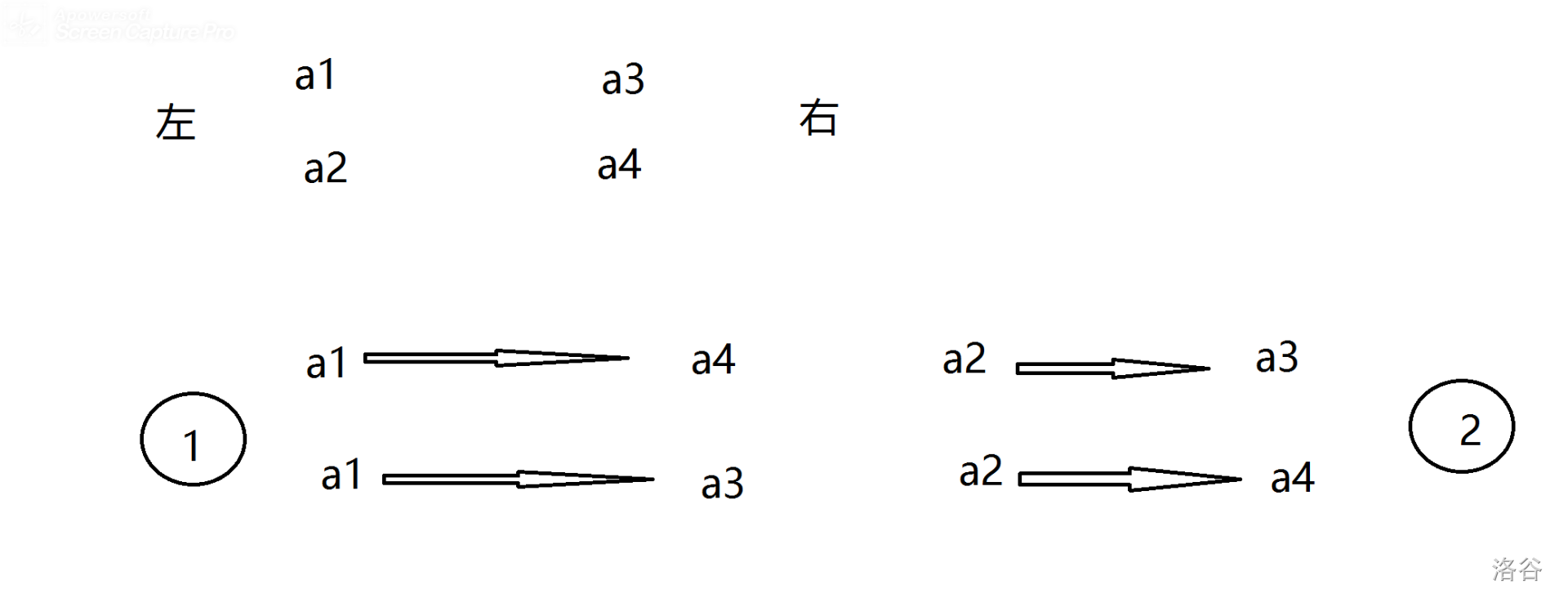
还有题目也说了**每个字母都有自己的编号**,所以肯定是$A$了。
注:$A$用于有序号,$C$用于没有序号,只考虑位置(如果还不理解$A$和$C$可以去百度)。
好了,分析到这就可以推出公式了,建议大家再回过头看看。
$\Large n!-\frac{n}{2}! * \prod\limits_{i=1}^{26}A(ni,\frac{ni}{2}) * nx
如果没有奇数个的字母$nx==1$就行了。
求$A$的时候可以用**费马小定理**求**逆元**。
$code$:
```c
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
int n,sum[30],s;
ll jc[2010],ans = 1;
char a[2010];
bool f;
ll q_pow(ll x,ll y)//用费马小定理求逆元,要用到快速幂。
{
ll ans = 1;
while(y)
{
if(y & 1) ans = ans * x % mod;
x = x * x % mod;
y >>= 1;
}
return ans;
}
void getjc()//可以预处理出阶乘数组。
{
jc[0] = 1;
for(int i = 1;i <= n;i++) jc[i] = (ll)jc[i - 1] * i % mod;
}
int main()
{
scanf("%d",&n);
scanf("%s",a + 1);
getjc();
for(int i = 1;i <= n;i++)
sum[a[i] - 'a' + 1]++;//预处理出每个字母出现的个数。
for(int i = 1;i <= 26;i++)
if(sum[i] != 0 && sum[i] % 2)//统计有没有奇数个字母。
{
if(f)//如果数量还>1,一定没法组成回文串,直接输出n!。
{
printf("%lld",jc[n]);
return 0;
}
f = 1;
s = sum[i]--;//字母奇数个出现的次数-1,因为那一个字母只能放到中间。
}
for(int i = 1;i <= 26;i++)//求A要用到逆元。
{
if(!sum[i]) continue;
ans *= (ll)jc[sum[i]] * q_pow(jc[sum[i] / 2],mod - 2) % mod;//逆元。
ans %= mod;
}
ans = ans * jc[n / 2] % mod;//公式。
if(f) ans = ans * s % mod;//如果有奇数别忘了乘nx,也就是s。
ans = jc[n] - ans;
if(ans < 0) ans += mod;//这里要注意,ans有可能是负数。
printf("%lld",ans);
return 0;
}
```
~~/管理员大大求过,$thanks$/~~