题解 P4471 【[BJWC2018]词韵】
三点水一个各
·
·
题解
本题出现公共后缀,考虑将所有单词放在一棵树里做。
什么是Trie
Trie 亦称字典树、前缀树,是一种以空间换时间的做法。
对于一个长度为 L 的字符串,插入和查询的复杂度均为 O(L)。
如图所示,将 \texttt{ab},\texttt{ad},\texttt{ace},\texttt{acf} 放入 Trie。
详细的 Trie 插入和查询操作请完成模板题P2580。
建树
观察本题,需要找到公共后缀,所以将单词反向存入 Trie,如图所示,将\texttt{ba},\texttt{da},\texttt{eca},\texttt{fca} 放入 Trie。
题面写到,序列中相邻两个单词需满足 LCS (A,B) ≥ \max(|A|,|B|)-1,所以相邻两个单词要么是父子关系,要么是兄弟关系,如:
$\texttt{abcd}$ 和 $\texttt{bbcd}$ 是兄弟关系(同理可以调换顺序,$\texttt{bbcd}$ 和 $\texttt{abcd}$ 也是合法的)。
所以,我们可以确定在图中的访问顺序是以下三种:访问父结点,访问子结点,访问同父的兄弟结点,如下图所示:
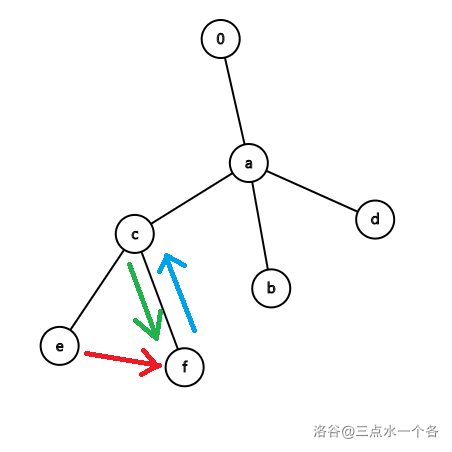
随后我们发现,在建树的过程中,不是所有结点都能按照如上三种顺序访问,如对 $\texttt{a},\texttt{ba},\texttt{dcba}$ 建树时,结点 $d$ 不能到结点 $c$,因为并不存在 $\texttt{cba}$ 这个单词,如图所示:
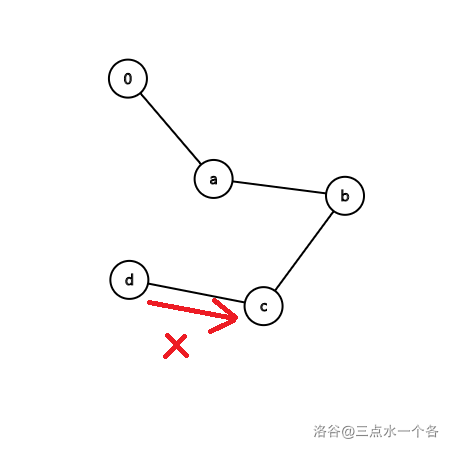
所以对于每个结点,我们用一个 $b$ 数组来存储他们出现的次数,当然,由于`所有单词互不相同`,这个数值只可能是 $0$ 或 $1$。
对 $\texttt{a},\texttt{ba},\texttt{dcba}$ 建树时,如图所示:
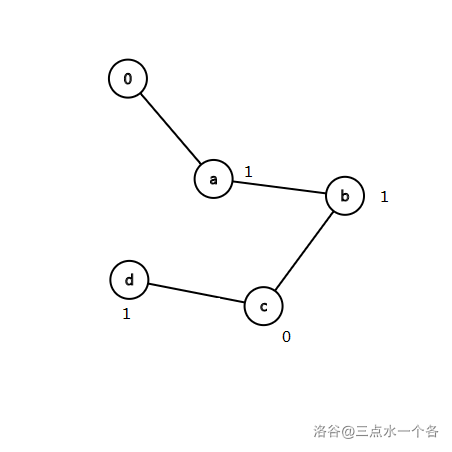
至此,建树完毕。
***
### 查找
我们知道,在查找过程中,因为出现次数为 $0$ 的点不可以被经过,所以不会出现 脱 节 的现象。
并且由于`所有单词互不相同`,所以不走回头路,即同一结点不经过 $2$ 次。
所以最后所有序列构成的图是一棵树而不是森林。
如图是对于 $\texttt{ba},\texttt{da},\texttt{eca},\texttt{fca}$ 一种可能的情况:
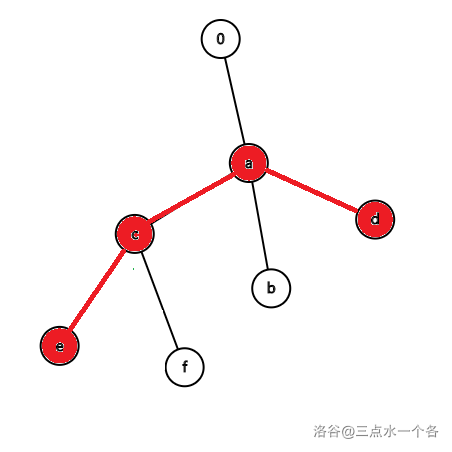
因此在一种可能的情况中,一个结点可能作为根结点,也可能是非根结点。
下面我先将情况**理想**化:
1. 所有结点 $i$ 所代表的单词次数均为 $1$,即 $b_i=1$。
2. 该结点是**非根结点**。
3. 不考虑该结点以上的结点(包括其父结点)
开一个数组,记 $i$ 结点作为非根结点时能取得最大单词数为 $f_i$。
首先,因为兄弟结点互相之间可以连接,并且访问顺序可以随意,在这里将所有的子节点 $j$ 都取来(取的是结点 $j$ 本身,而不是 $f_j$)。
然后,思考对于 $i$ 的子结点 $j$,在访问到 $j$ 之前,肯定是由 $j$ 以下的结点过来的,也就是由 $f_j$ 个结点过来的,要使 $f_i$ 最大,就得找到最大的 $f_j$。
(这里 $i,j,f_i,f_j$ 的关系有点复杂,总之就是 $j$ 是 $i$ 的子结点,$f_{i/j}$ 是 $i/j$ 作为非根结点时能取得最大单词数,请读者自行梳理)。
最后可以取到 $i$ 结点本身,不要漏掉。
设 $i$ 有 $k$ 个子结点,那么
$$f_i=\max(f_j-1)+k+1$$
至于为什么是 $f_j-1$ 而不是 $f_j$,是因为 $j$ 在 $f_j$ 和 $k$ 中均出现一次。
举个例子:
对于单词 $\texttt{ba},\texttt{da},\texttt{eca},\texttt{fca},\texttt{ica},\texttt{heca},\texttt{geca},\texttt{jfca}$,以 $\texttt{c}$ 为非根结点时,如图所示:
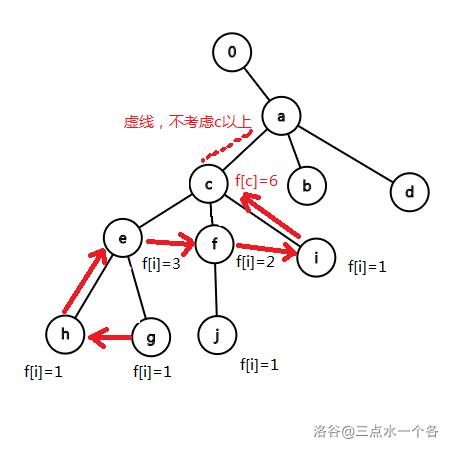
解释一下,此图中,$c$ 子节点个数 $k=3$,子节点($\texttt{e}$,$\texttt{f}$,$\texttt{i}$)中最大的 $f$ 为 $3$,故 $f_c=\max(f_j-1)+k+1=(3-1)+3+1=6$。
为什么 $f_c$ 只能取子结点 $j$ 中最大的一个 $f$ 而不是取多个?
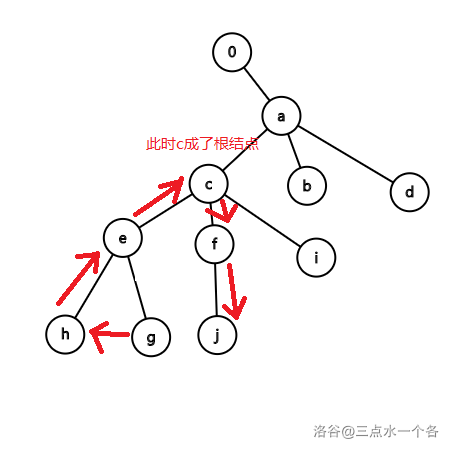
因为如果取第二个,意味着从一个叶子结点(如 $\texttt{h}$,$\texttt{g}$ )经过 $\texttt{c}$ 到另一个叶子结点(如$\texttt{j}$),此时无法再从叶子结点往上,因为`所有单词互不相同`,那么此时,$\texttt{c}$ 就成了根节点,与我的假设不符。如图所示:
***
接下来考虑当该结点为根结点:
上面分析非根结点说过,如果取第二个,意味着该结点就是根结点。
所以以该点为根节点时,最大单词个数是在以该单词为非根结点的基础上,再加上第二大的 $f_j$,即:
$$f'_{i}=max1(f_j-1)+max2(f_j-1)+k+1$$
***
接下来考虑该结点对应单词个数为 $0$,即 $b_i=0$:
对于一个对应单词个数为 $0$ 的结点,不能将它忽略。
因为如果他存在对应单词个数不为 $0$ 的子结点,即 $b_j=1$。
这些 $b_j=1$ 的子结点之间扔可以相互访问,
这是只需要把公式中最后加上去的 $1$ 删掉就可以了。
### 复杂度
设单词个数为 $N$,长度之和为 $S$。
建树复杂度 $O(s)$。
查找复杂度 $O(26N)$。
$\mathtt{Code}
#include<bits/stdc++.h>
using namespace std;
int a[2000003][27],b[2000003],f[2000003];//3e6似乎要炸
int n,m,l1,l2,num=0,ans=0;
string s;
int main()
{
scanf("%d",&n);
memset(a,0,sizeof(a));
for(int k=1;k<=n;++k) //Trie 建树
{
int x=0;
cin>>s;
for(int i=s.length()-1;i>=0;--i)
{
if(!a[x][s[i]-'a'])
a[x][s[i]-'a']=++num;
x=a[x][s[i]-'a'];
}
b[x]++; //单词个数
}
for(int i=num;i>=0;--i)
{
f[i]=b[i]; //该节点单词个数,是1或是0
l1=l2=0; //最大和次大
for(int j=0;j<=25;++j)
if(b[a[i][j]]) //存在该子结点,若该结点对应单词数为0,没有意义。
{
f[i]++; //选取子结点本身
if(f[a[i][j]]-1>l1) l2=l1,l1=f[a[i][j]]-1; //更新最长
else if(f[a[i][j]]-1>l2) l2=f[a[i][j]]-1;//更新次长
}
f[i]+=l1; //非根结点最多单词
ans=max(ans,f[i]+l2); //根节点最多单词。
}
printf("%d",ans);
return 0;
}