题解 P3788 【幽幽子吃西瓜】
离散小波变换°
·
·
题解
## 题目大意
> 有一个 $\stackrel{\texttt{suika}}{\small\textsf{西瓜}}$ 。现在挖去俯视图上 $[a\degree,b\degree]$ 这一块(特别地,若 $a>b$ ,则是挖去 $[a\degree,360)\cap[0,b]$),询问主视图中红色部分占可见部分的比例。
> $T$ 组数据。 $1\le T\le 10^4;0\le a,b<360$ 且 $a,b\in \Bbb{Z};a\neq b$ 。
## 题解
### 前置知识
由于我们要求出看到的西瓜的面积,所以把切面转换到主视图非常重要。
> 令投射线通过点或其他物体,向选定的投影面投射,并在该面上得到图形的方法称为投影法。
> $$\kern{1pt}\tag*{\small\text{——百度百科}}$$
> 考虑这样的图形:
> 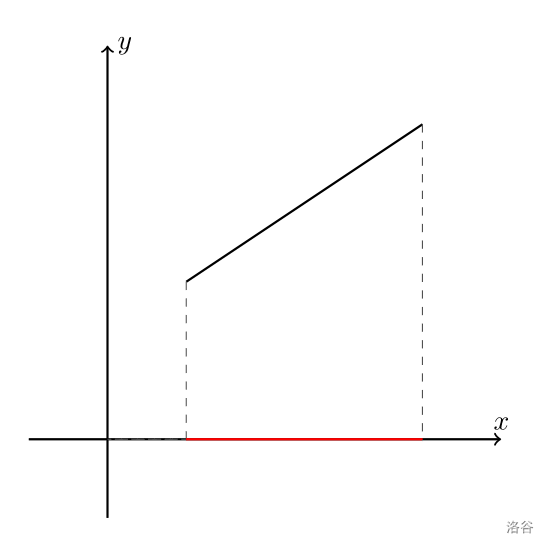
> 这就是一个非常简单的将直线投影到 $x$ 轴上的例子。
我们要做的就是把一个圆投影到平面上,并且计算出它的面积。关于投影,有一个非常重要的结论:**投影后的图片的面积,就是投影前的面积乘上夹角的余弦值**。显然这个结论对于矩形成立,而我们可以类比微分,把一个圆分成无数个矩形再分别投影。因此我们根据俯视图上,一个圆与主视图的夹角就可计算出这个圆在主视图上的面积。
此外,下文还会用到**弧度制**。在角度制里,一个完整的圆对应的度数是 $360\degree$,而弧度制里这个值是 $2\pi$。将角度制转换为弧度制非常简单,对于角度制下的数值 $a$ ,转换为弧度制就是 $\dfrac{a}{360}\times 2\pi=\dfrac{a}{180}\pi$。
在讨论各种复杂情况之前,我们先考虑一个更加简单的问题,也就是 $a,b\in[0,180)$ 的情况,并且我们**仅考虑主视图右半部分**。这种情况同样可以细分分为两类,每类三种。在下文中,我们认为西瓜的半径为 $1$,这显然不会影响答案。
- **第一类**: $a<b$ 。观察下面三张图:
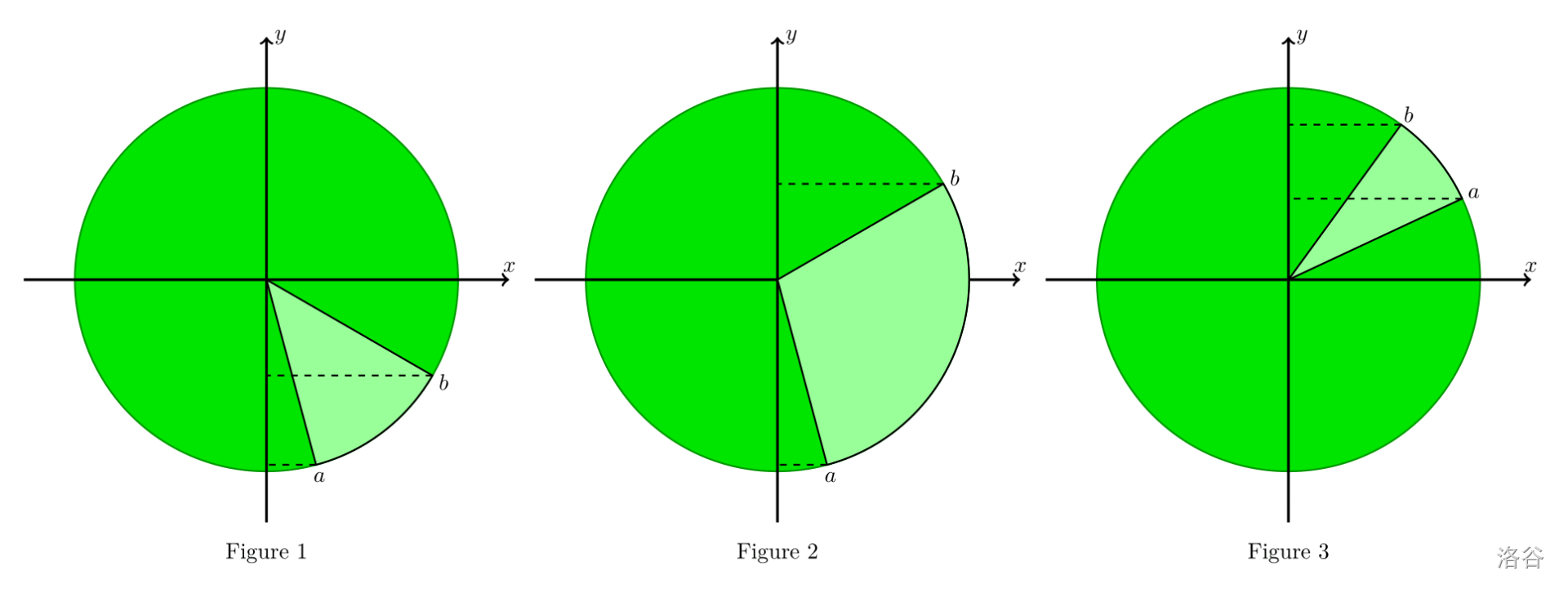
- 第一种情况, $a,b\in[0,\dfrac{1}{2}\pi)$。此时可视范围是 $\dfrac{1}{2}\pi$,瓜瓢部分为 $\dfrac{1}{2}\pi(\cos(b)-\cos(a))$。
- 第二种情况, $a\le \dfrac{1}{2}\pi\le b$。此时可视范围是 $\dfrac{1}{2}\pi\max\{\cos(a),\cos(b)\}$,瓜瓢部分是 $\max\{0,\dfrac{1}{2}\pi(\cos(b)-\cos(a))\}$。
- 第三种情况, $a,b\in[\dfrac{1}{2}\pi,\pi)$。此时可视部分是 $\dfrac{1}{2}\pi$,看不到瓜瓢。
- **第二类**: $a>b$ 。同样地,有三张图:
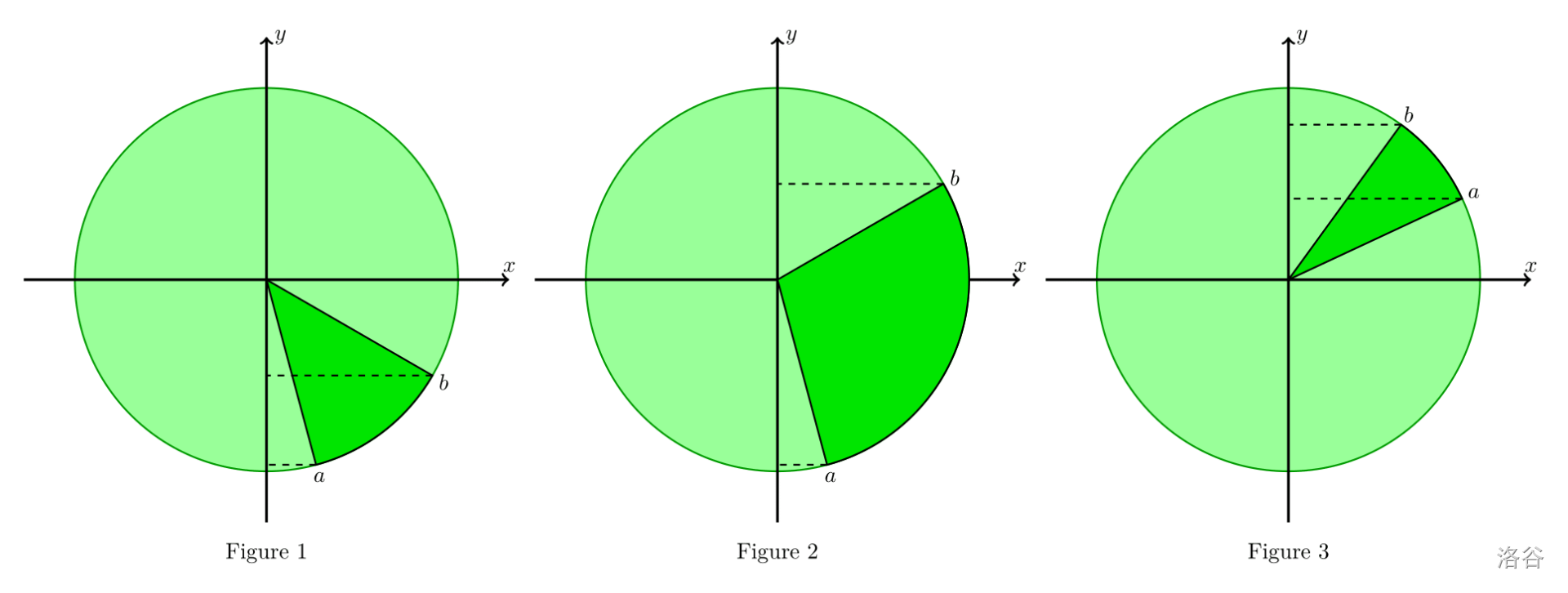
- 第一种情况, $a,b\in[0,\dfrac{1}{2}\pi)$。此时可视部分是 $\dfrac{1}{2}\pi \cos(b)$,瓜瓢部分是 $\dfrac{1}{2}\pi \cos(a)$。
- 第二种情况, $a\le \dfrac{1}{2}\pi\le b$。此时可视部分是 $\dfrac{1}{2}\pi$,瓜瓢部分是 $\dfrac{1}{2}\pi\cos(a)$。
- 第三种情况, $a,b\in[\dfrac{1}{2}\pi,\pi)$。此时可视部分与瓜瓢部分相同,同样是 $\dfrac{1}{2}\pi\cos(a)$。
讨论完了这么多情况,快快封装到一个函数里吧。
---
显然,左半边的情况应当与右半边相似。我们只要想办法关于 $x$ 轴翻转即可。一般地,对于左边的角度 $\theta$,翻到右边变成 $\theta'$,应该有:
$$\theta-\pi=\pi-\theta'$$
因此 $\theta'=2\cdot \pi-\theta$。下面开始最终的讨论。
- $a,b$ 都在同一个半圆(即同在 $[0,\pi)$ 或者同在 $[\pi,2\pi)$ 内)。这个时候,对于同时处在的半圆,直接套用刚刚的大讨论。如果 $a<b$,那么另外一个半圆可视部分就是 $\dfrac{1}{2}\pi$,看不到瓜瓢;否则另外一个半圆无可视部分和瓜瓢部分。
- $a,b$ 在分别两个半圆当中。那么把这部分拆成两块,每块都相当于在一个半圆上挖去了一块,所以丢回刚刚的大讨论就行了。
## 参考代码
```cpp
#include<bits/stdc++.h>
#define up(l,r,i) for(int i=l,END##i=r;i<=END##i;++i)
#define dn(r,l,i) for(int i=r,END##i=l;i>=END##i;--i)
using namespace std;
const double pi =acos(-1);
double l,r;
void slv(double s,double t,bool f){ //l/r
if(t<=0.5*pi){
if(f) l+=sin(s),r+=sin(t); else l+=(sin(t)-sin(s)),r+=1;
}else if(0.5*pi<=s){
if(f) l+=sin(s),r+=sin(s); else r+=1;
} else{
if(f) l+=sin(s),r+=1;
else l+=max(0.0,sin(t)-sin(s)),r+=max(sin(s),sin(t));
}
}
int main(){
int T; scanf("%d",&T); up(1,T,TT){
double a,b; scanf("%lf%lf",&a,&b); l=r=0,a=pi*a/180,b=pi*b/180;
if(a<=pi&&b<=pi){
if(a<b) slv(a,b,0),r+=1; else slv(b,a,1);
} else if(a>pi&&b>pi){
if(a<b) slv(2*pi-b,2*pi-a,0),r+=1;
else slv(2*pi-a,2*pi-b,1);
} else {
if(a<b) slv(a,pi,0),slv(2*pi-b,pi,0);
else slv(0,b ,0),slv(0,2*pi-a,0);
}
printf("%.1lf%%\n",100.0*l/r);
}
return 0;
}
```
$$%偷偷藏个图片源码,没人发现吧
%\documentclass[UTF-8,border=10pt]{standalone}
%\usepackage{listings,xcolor,tikz}
%\usetikzlibrary{calc}
%\newcommand{\suika}[2]{
% \filldraw[fill=green!40!white,draw=green!60!black,thick] (0,0) circle (3);
%
% \draw[very thick,->] (-3.8,0) -- (3.8,0);
% \draw[very thick,->] (0,-3.8) -- (0,3.8);
% \node[anchor=south] at (3.8,0) {$x$};
% \node[anchor=west ] at (0,3.8) {$y$};
%
% \coordinate (O) at (0,0);
% \coordinate (A) at (#1:3);
% \coordinate (B) at (#2:3);
%
% \filldraw[fill=green!90!black,thick] (0,0) -- (A) arc(#1:#2:3) -- (0,0);
% \node at ($(A)+(#1:0.2)$) {$a$};
% \node at ($(B)+(#2:0.2)$) {$b$};
%
% \draw[dashed,thick] (A) -| (O) (B) -| (O);
%}
%\begin{document}
% \begin{tikzpicture}
% \begin{scope}
% \suika{-75}{-30}; \node[anchor=north] at (0,-4) {Figure 1};
% \end{scope}
% \begin{scope}[xshift=8cm]
% \suika{-75}{ 30}; \node[anchor=north] at (0,-4) {Figure 2};
% \end{scope}
% \begin{scope}[xshift=16cm]
% \suika{ 25}{ 54}; \node[anchor=north] at (0,-4) {Figure 3};
% \end{scope}
%\end{tikzpicture}
%\end{document}
$$