题解 P4496 【[CTSC2009]移民站选址】
disangan233
·
·
题解
前言
- 这是本蒟蒻的第一篇黑题题解,有误请轻喷。
- 更良好的观看体验:disangan233の博客
- PS:这题本蒟蒻因为某个数组连续开小找了两天两夜。
- 请勿抄袭代码。
(反正你代码又交不过)
- 于 2020/10/7修订。
题意简述
- 给你坐标系上 n 个点 a_i(i\in \{1 \cdots n\}) 的坐标,让你求出新建 m 个节点 b_i(i\in \{1 \cdots m\})(可与已存在点重合)后,求 a_i 到 b_i 的最小费用最大流,并输出方案。
具体实现
首先,将题目仔细分析后,得出这样一个结论:
设新节点为 c,为了满足最优解,必定满足:
x_c \in \{ x_i|i \in [1,n]\},y_c \in \{ y_i|i \in [1,n]\}
所以我们把原题就可以拆成横纵坐标来做。
输入1
显然这就是一个带权中位数,不懂的可以去看一维邮局问题。
可以将题意转换为给你 w_i,d(i,j) 为 a_i 到 a_j 的距离,求
\min \left\{ \sum_{j=1}^{n} w_j \times d(i,j)| i\in [1,n] \right\}
先假设 w_i 不存在,那么题目就让你求
\min \left\{ \sum_{j=1}^{n} d(i,j)| i\in [1,n] \right\}
显然可以将 x_{a_i} 和 y_{a_i} 分别排序,求出中位数后枚举即可。
那么带权值的中位数即可在普通中位数的前提下,将 a_i 的个数修改为 w_i 即可。
上个图吧:
输入 2-10
首先先考虑跑最小费用最大流,发现 B(i,j) 不好实现,于是考虑转换模型。
以 b_i 建立新节点,并将 b_i 拆成 n+1 个点 b_{i,j}(j\in [1,n+1] ),表示状态 b_i 建在a_j上。
对于每一个 b_{i,j},向 b_{i,j+1} 建一条流量为 dis(i,j) 的双向边,向 b_{k,j} 建一条流量为 B(i,j)的双向边。
然后将源点向 b_{i,1},b_{i,n+1} 向汇点,建一条流量为 \infty 的边。
这时将对于横纵坐标不同的 $dis(i,j)$ 建图跑两次最小割,答案即为两次最小割之和。
上个图(黄边是双向边,画错了):
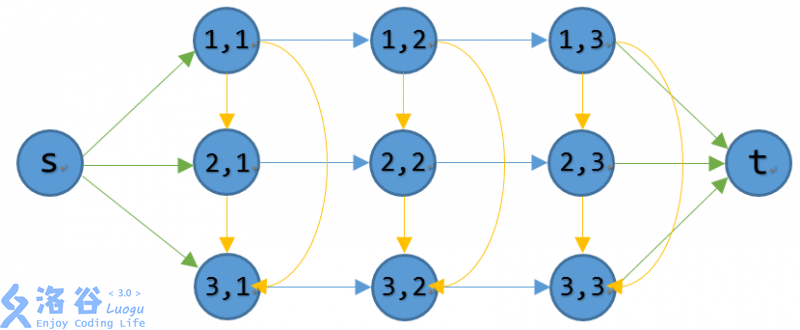
图中 $n=2,m=3$,绿色为 $\infty$,蓝色为 $dis(i,j)$,橙色为 $B(i,j)$。
#### 输出方案
显然,在跑完最小割后的残流网络中,横向割边的出点即为答案所在的横(或纵)坐标。
这时候对于 $s$,$t$,正反跑两次 dfs,将必定割边存入$ans$ 即可。
但是这样你发现输入 7 会过不了!冷静分析后发现,必定割边的数量有可能小于 $m$!
于是在疯狂的尝试后,你发现了所有的可能割边均可为答案,只跑源点即可。
---
#### 正确性证明
献上这个熟悉的图:
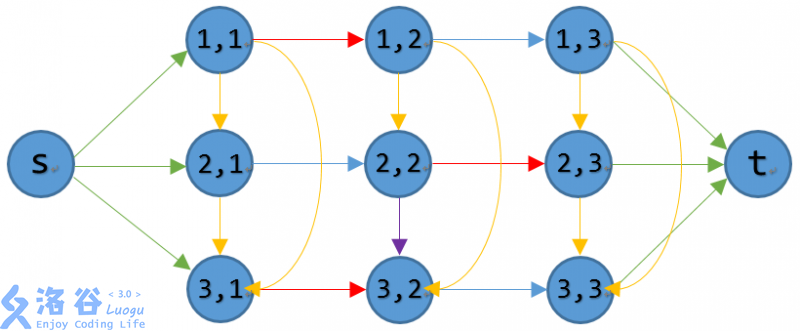
我们令红色边为影响方案决策的满流边,此时的最小割集中,为了割掉 $s$ 和 $t$,我们发现紫色边也应该跟着一起满流,就满足了跑 $B(2,3)$ 的性质。
所以在 $a_i$,$b_i$ 可重复的条件下,此建图方法正确。
### 温馨提示
你指望你的网络流能 1s 跑过 $n=m=100$ 的数据?
醒醒!这是提交答案题!
### 源代码
远古码风,有空再改。
```cpp
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define ak *
#define fp(x,y) for(re i=1;i<=x;i++) for(re j=1;j<=y;j++)
#define inf 1e18
int bj,tot,cnt=1,n,m,k,s,t,h[100005],dis[100005],l,r,q[100005],tt[2],wtf=233;
int cur[100005],ansx[100005],ansy[100005],vis[100005];
ll w[100005],nx[100005],ny[100005],gx[305][305],gy[305][305],a[305][305],b[305][305],ans;
struct did{
int u,next,to;
ll f;
}e[2000005];
struct node{
ll pos,val;
bool operator <(node a) const {return pos<a.pos;}
}x[100005],y[100005];
char qwq,mp;
inline ll id(re x,re y) {return (x-1)*(n+1)+y;}
inline ll read()
{
ll cz=0,ioi=1;qwq=getchar();
while(qwq<'0'||qwq>'9') ioi=qwq=='-'?~ioi+1:1,qwq=getchar();
while(qwq>='0'&&qwq<='9') cz=(cz<<3)+(cz<<1)+(qwq^48),qwq=getchar();
return cz ak ioi;
}
inline void add(re x,re y,ll z)
{
e[++cnt]=(did){x,h[x],y,z},h[x]=cnt;
e[++cnt]=(did){x,h[y],x,0},h[y]=cnt;
}
inline int bfs(re u)
{
memset(dis,-1,sizeof(dis));dis[u]=0;
l=r=0;q[++r]=u;
while(l<r)
{
re i=q[++l];
if(i==t) return 1;
for(re j=h[i],k;k=e[j].to,j;j=e[j].next)
if(dis[k]<0&&e[j].f)
dis[k]=dis[i]+1,q[++r]=k;
}
return 0;
}
inline ll dfs(re u,ll maxf)
{
ll res=0;
if(u==t||maxf==0) return maxf;
for(re &i=cur[u],v;v=e[i].to,i;i=e[i].next)
if(e[i].f&&dis[v]==dis[u]+1)
{
ll delta=dfs(v,min(maxf,e[i].f));
e[i].f-=delta;e[i^1].f+=delta;
res+=delta;maxf-=delta;
if (!maxf) return res;
}
if (maxf!=res) dis[u]=-2;
return res;
}
inline ll dinic()
{
ll ans=0;
while(bfs(s))
{
for(re i=s;i<=t;i++) cur[i]=h[i];
ans+=dfs(s,inf);
}
return ans;
}
inline ll calc(re a,re b)
{
return abs(nx[a]-nx[b])+abs(ny[a]-ny[b]);
}
void find(re u,re k)
{
vis[u]=k;tt[k]++;
for(re i=h[u],v;v=e[i].to,i;i=e[i].next)
if(e[i].f&&!vis[v]) find(v,k);
}
int main()
{
freopen("locate9.in","r",stdin);
freopen("data.out","w",stdout);
n=read(),m=read();s=0,t=m*(n+1)+1;
for(re i=1;i<=n;i++) x[i].pos=nx[i]=read(),y[i].pos=ny[i]=read();
if(m==1)
{
ll res=0,xx,yy,sum=0,pre=0;
for(re i=1;i<=n;i++) sum+=(x[i].val=y[i].val=w[i]=read());
sum=(sum&1)?sum/2+1:sum/2;
sort(x+1,x+n+1);sort(y+1,y+n+1);
for(re i=1;i<=n;i++)
{
if(pre+x[i].val>=sum) {xx=x[i].pos;break;}
pre+=x[i].val;
}
pre=0;
for(re i=1;i<=n;i++)
{
if(pre+y[i].val>=sum) {yy=y[i].pos;break;}
pre+=y[i].val;
}
for(re i=1;i<=n;i++) res+=w[i]*(abs(xx-nx[i])+abs(yy-ny[i]));
printf("%lld\n%lld %lld\n",res,xx,yy);
return 0;
}
sort(nx+1,nx+n+1);sort(ny+1,ny+n+1);
fp(n,m) a[i][j]=read();
for(re i=1;i<m;i++) for(re j=i+1;j<=m;j++) b[i][j]=b[j][i]=read();
fp(m,n) for(re k=1;k<=n;k++)
{
gx[i][j]+=abs(nx[j]-x[k].pos)*a[k][i];
gy[i][j]+=abs(ny[j]-y[k].pos)*a[k][i];
}
for(re i=1;i<=m;i++)
{
for(re j=1;j<=n;j++) add(id(i,j),id(i,j+1),gx[i][j]);
add(s,id(i,1),inf),add(id(i,n+1),t,inf);
}
for(re i=1;i<m;i++)
for(re j=i+1;j<=m;j++)
for(re k=2;k<=n;k++)
{
ll now=b[i][j]*(nx[k]-nx[k-1]);
add(id(i,k),id(j,k),now);e[cnt].f=now;
}
ans+=dinic();find(s,1);
fp(m,n) for(re k=h[id(i,j)];k;k=e[k].next)
if(!e[k].f&&vis[id(i,j)]&&!vis[id(i,j+1)]&&e[k].to==id(i,j+1)) ansx[++ansx[0]]=nx[j];
cnt=1;memset(h,0,sizeof(h));s=0;t=m*(n+1)+1;
for(re i=1;i<=m;i++)
{
for(re j=1;j<=n;j++) add(id(i,j),id(i,j+1),gy[i][j]);
add(s,id(i,1),inf),add(id(i,n+1),t,inf);
}
for(re i=1;i<m;i++)
for(re j=i+1;j<=m;j++)
for(re k=2;k<=n;k++)
{
ll now=b[i][j]*(ny[k]-ny[k-1]);
add(id(i,k),id(j,k),now);e[cnt].f=now;
}
ans+=dinic();memset(vis,0,sizeof(vis));find(s,1);
fp(m,n) for(re k=h[id(i,j)];k;k=e[k].next)
if(!e[k].f&&vis[id(i,j)]&&!vis[id(i,j+1)]&&e[k].to==id(i,j+1)) ansy[++ansy[0]]=ny[j];
printf("%lld\n",ans);
for(re i=1;i<=m;i++) printf("%d %d\n",ansx[i],ansy[i]);
return 0;
}
```