题解 P3748 【[六省联考2017]摧毁“树状图” 】
Krystallos
·
·
题解
UPD 2021/3/23: 代码贴错的问题终于有人指出来了
我个人非常不理解考场上为什么会出现这么**的动规,真就推式子一小时写码十分钟呗
24分,x=2
不会真的有人不会照着给出的方案模拟然后统计答案吧不会吧不会吧
另24分,x=1
关于这个部分分小编也没想出来怎么做,有知道的小伙伴可以在评论区留言哦
100分
我们非常的勇认为我们可以不需要靠给出的方案直接算正解(
对于每个节点 p 我们定义四个状态 f_{p, 0 \sim 3},下面我们将对每个状态分别解释含义 (只是演示切除链的形态,不代表这么切最优)
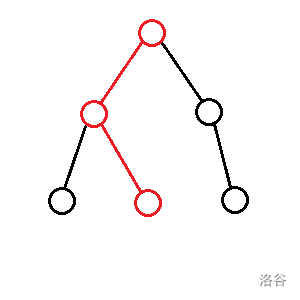
$f_{p, 1}$:切除一条两个端点在 $p$ 子树内且链不经过 $p$ 的链的答案:
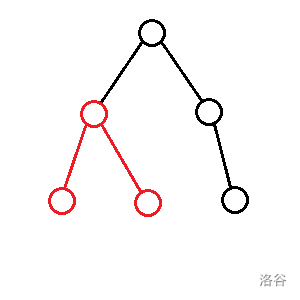
$f_{p, 2}$:切除一条两个端点在 $p$ 子树内且经过 $p$ 的链的答案:
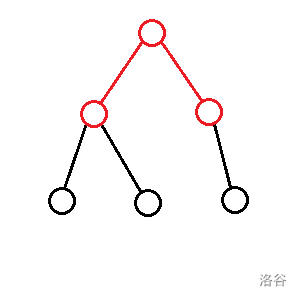
$f_{p, 3}$:切除一条端点在 $p$ 且另一端点在子数内的链与一条两个端点在 $p$ 子树内且经过 $p$ 的链的答案:
~~以下内容可能引起不适请谨慎观看~~
对于每个讨论到的节点 $p$ ,枚举其的儿子 $son$,假设已经将 $son$ 的状态讨论完毕,那么现在有一下六种情况可以更新答案:
* $f_{p, 3} + f_{son, 0} - (p == 1)$(因为如果 $p$ 是 $1$ 那么上方没有其他连通块要减掉 $1$,之后同理): 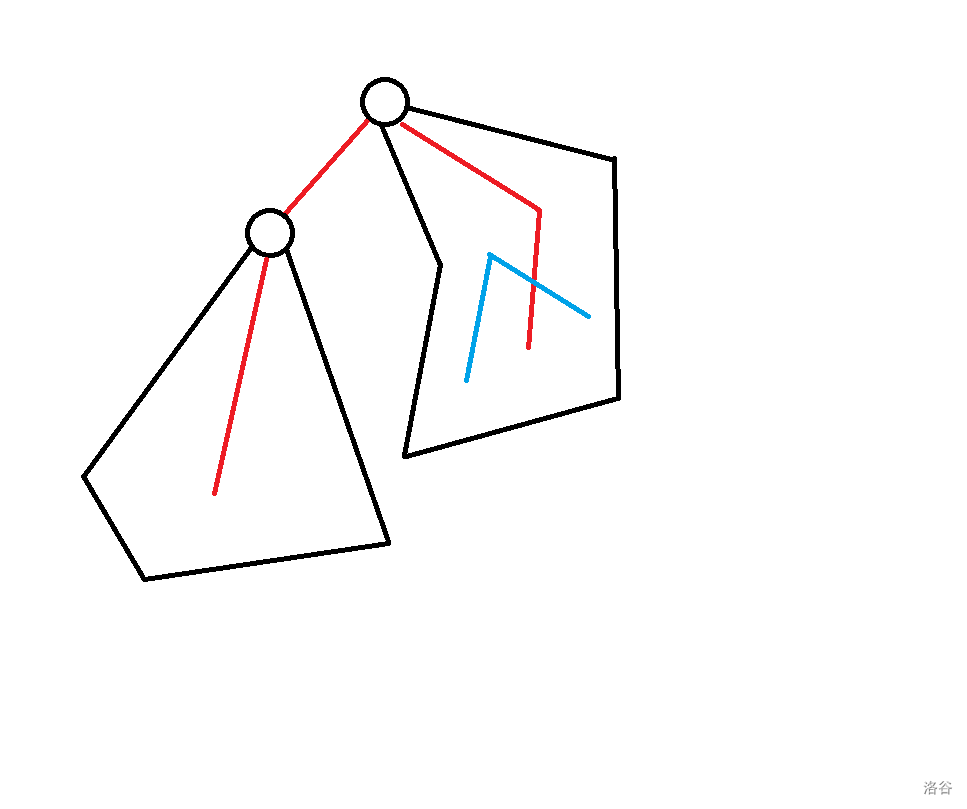 ~~画图逐渐抽象~~
* $f_{p, 0} + f_{son, 3} - (p == 1)$: 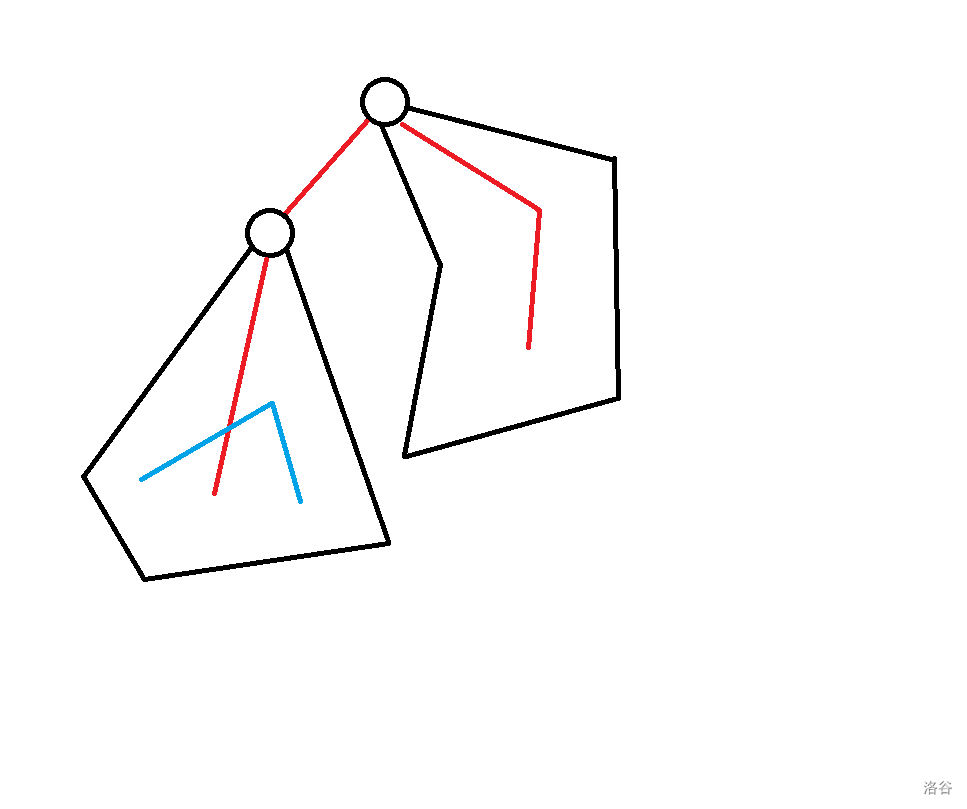
* $f_{p, 1} + f_{son, 2}$(因为无论 $p$ 上方有没有节点都不影响答案所以不需要判 $p$ 为 $1$): 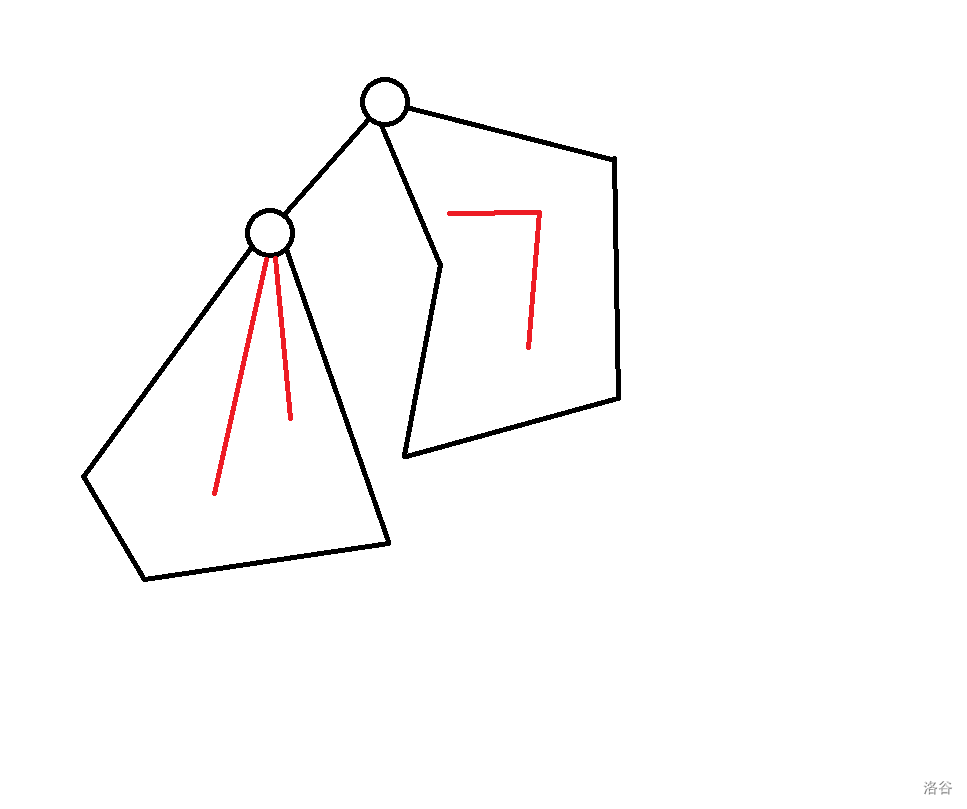
* $f_{p, 1} + f_{son, 1} - 1$(上方没切到的地方连到一起了多算了一个要减一): 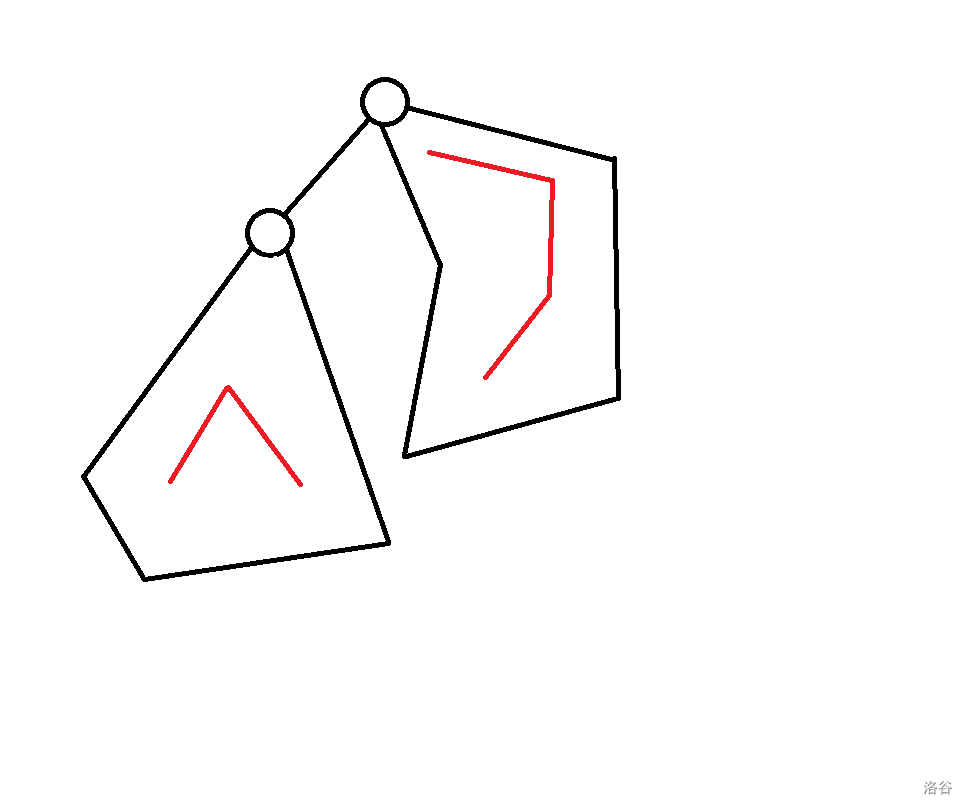
* $f_{p, 2} + f_{son, 1} - (p == 1)$: 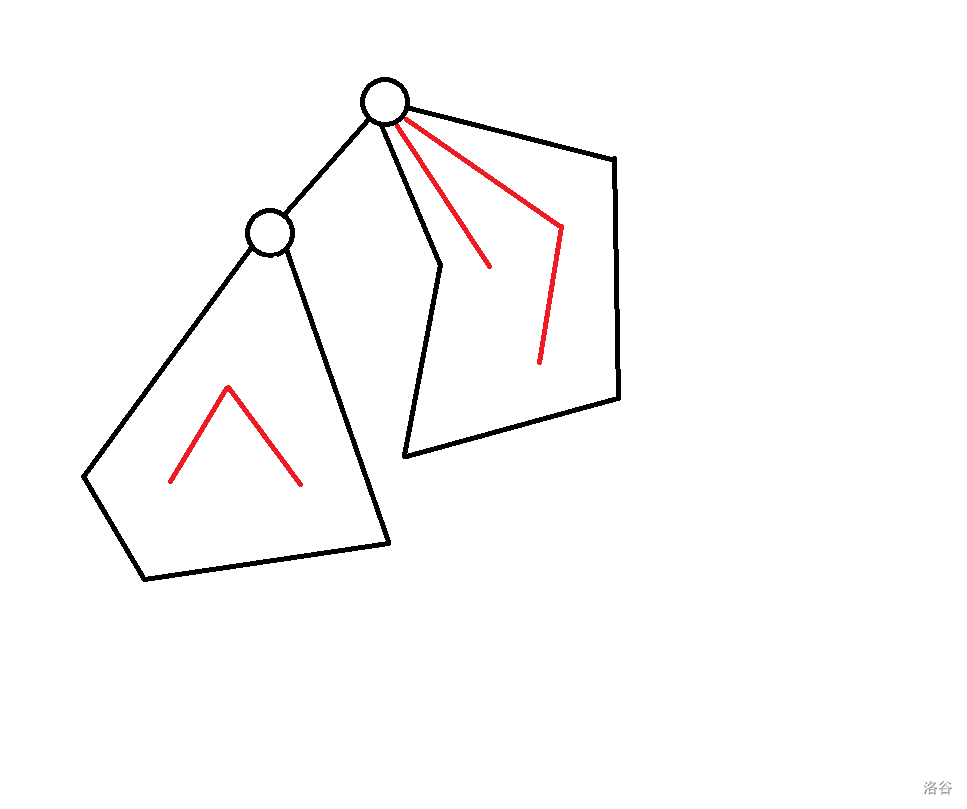
* $f_{p, 2} + f_{son, 2} - (p == 1)$: 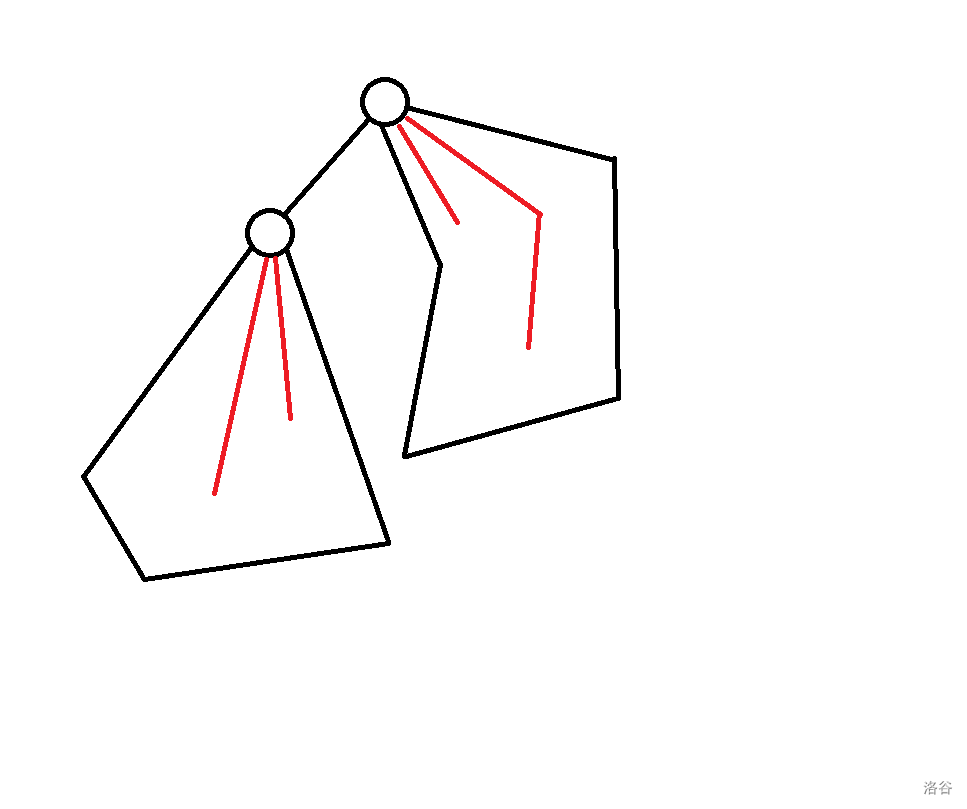
~~坐下,这才刚开始呢,继续往下看~~
有一种方案可以推得 $f_{p, 0}$,即直接在 $f_{son, 0}$ 的基础上删掉节点 $p$,$f_{son, 0} + deg_p - 1$(其中 $deg_p$ 的意思是 $p$ 的儿子数):
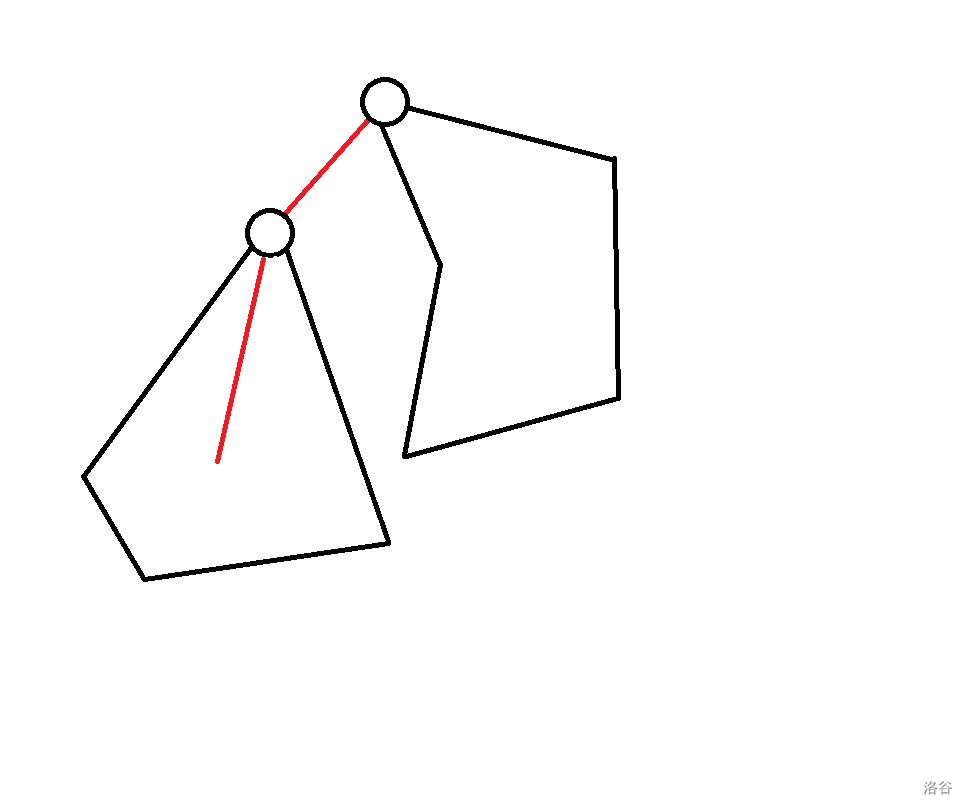
有两种方案可以推得 $f_{p, 1}$:
$f_{q, 1}$(直接继承):
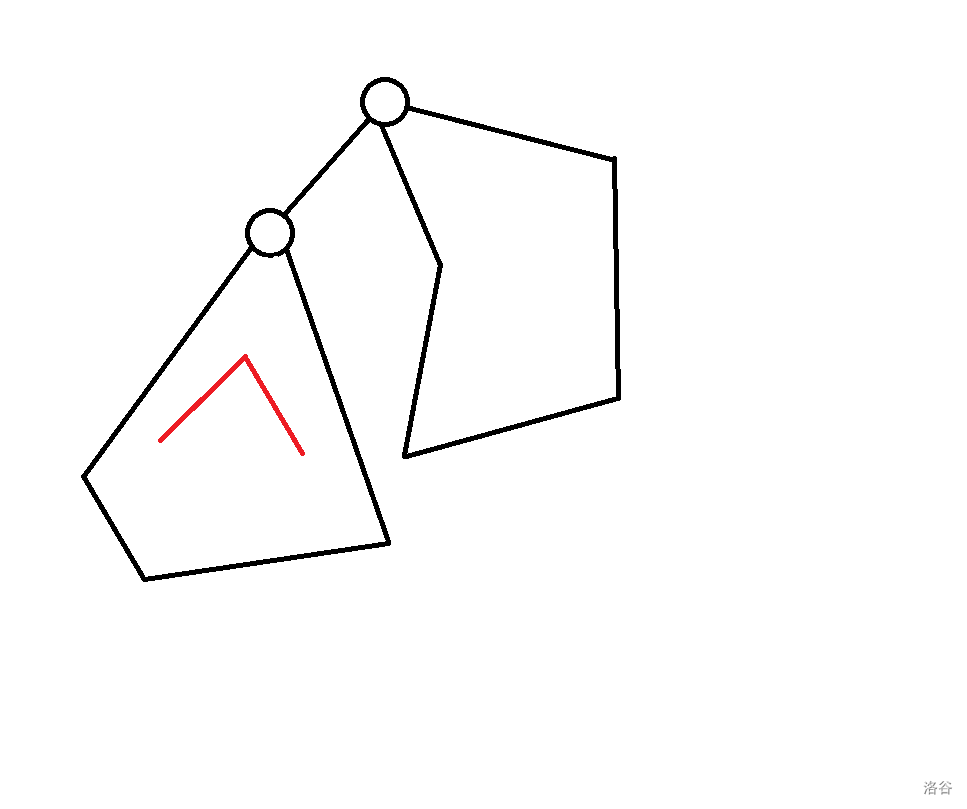
$f_{q, 2} + 1$:
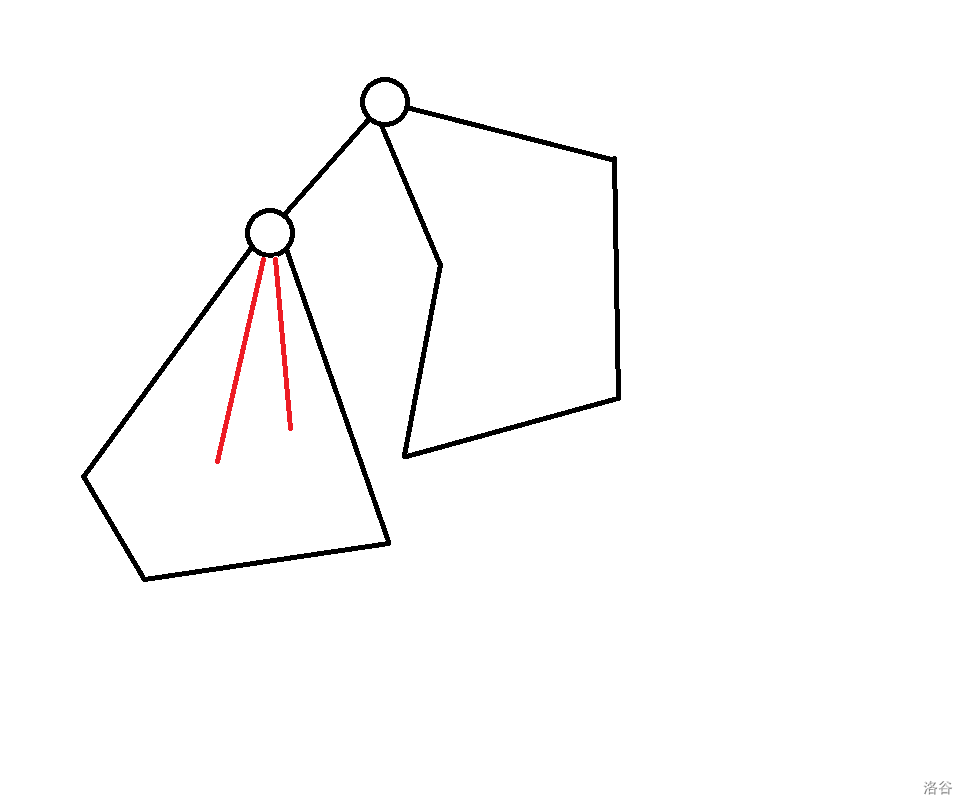
有一种方案可以推得 $f_{p, 2}$,即$f_{p, 0} + f_{q, 0} - 1$:
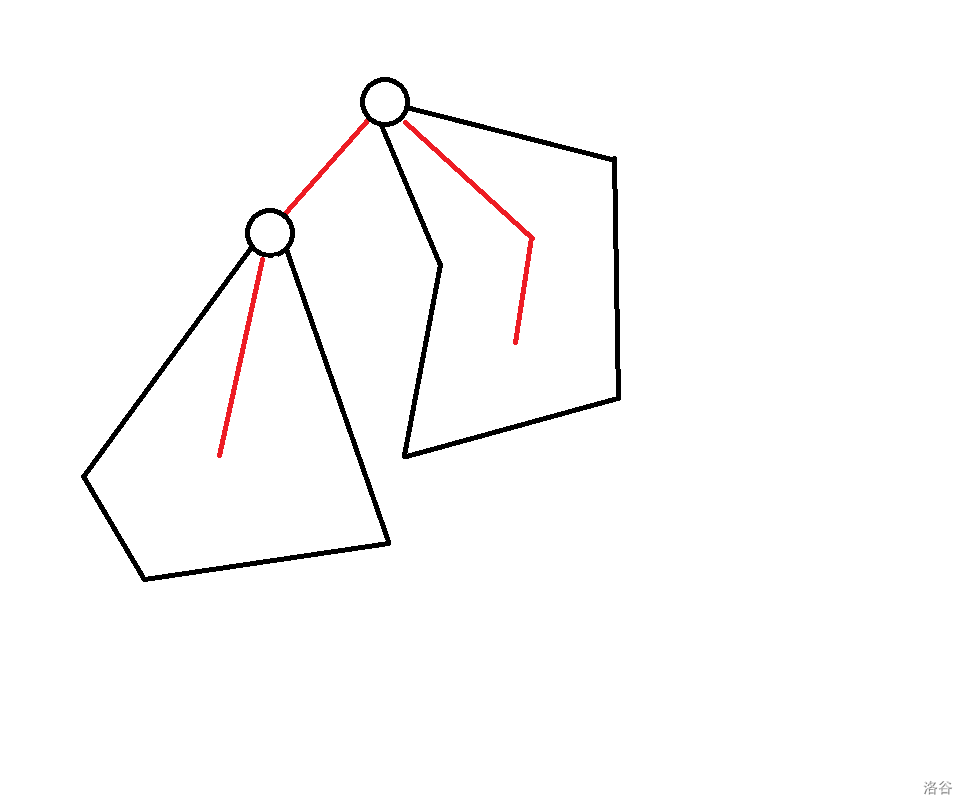
~~要来力(~~
有五种方案可以推得 $f_{p, 3}$ ~~(惊不惊喜意不意外)~~:
$f[p][0] + f[q][2] - 1$:
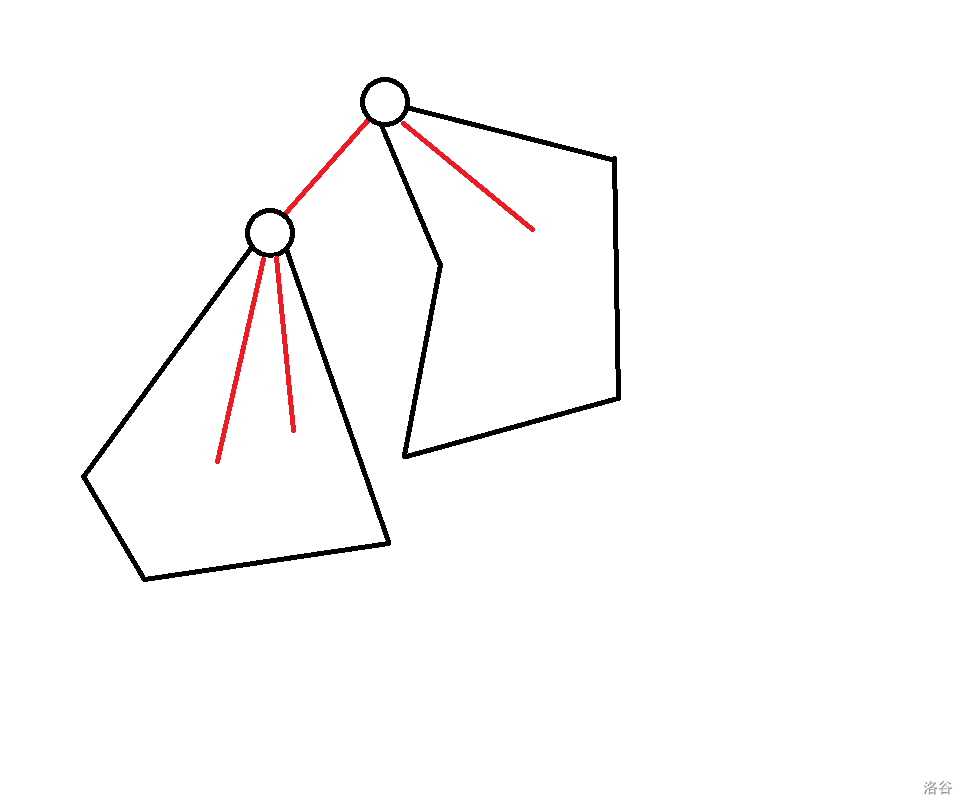
$f[p][0] + f[q][1] - 1$:
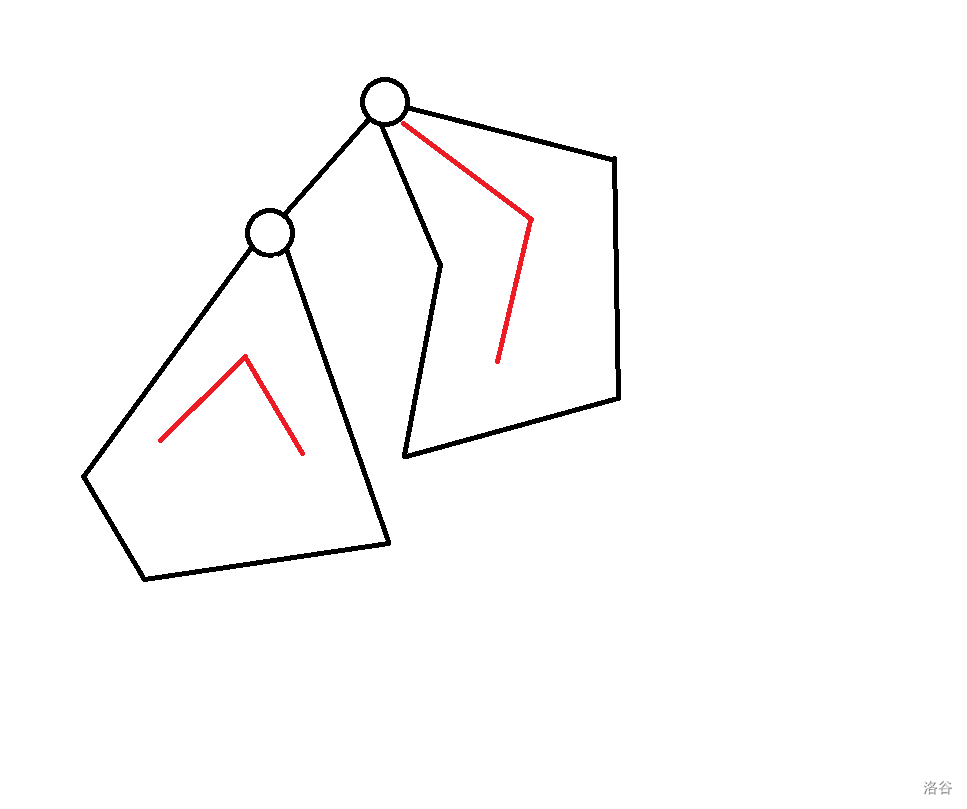
$f[p][2] + f[q][0] - 1$:
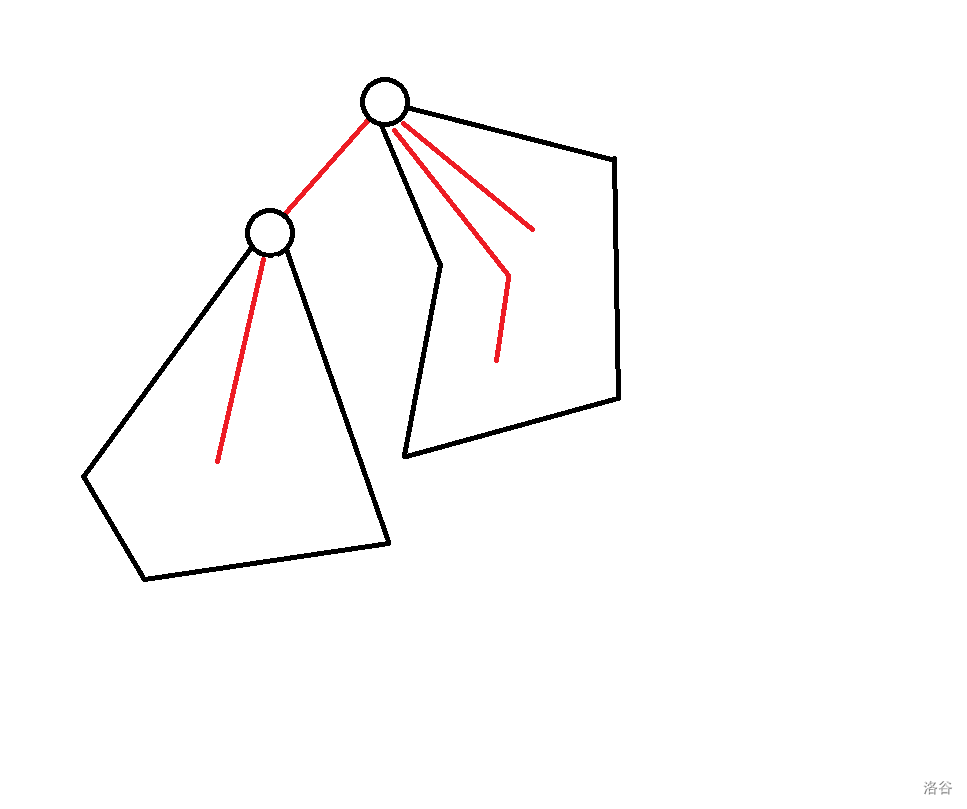
$f[q][3] + deg[p] - 1$:
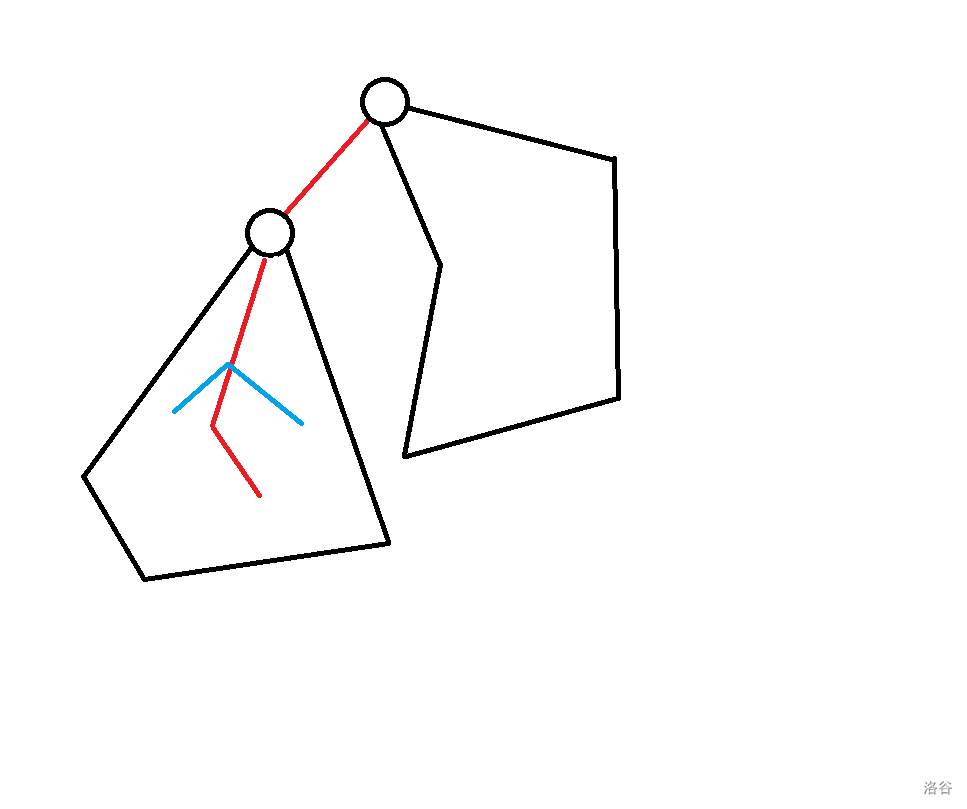
$f[q][0] + deg[p] + ret - 2$:
($ret$ 的意思是之前讨论的儿子 $q$ 中最大的 $f_{q, 1}$ 和 $f_{q, 2}$)
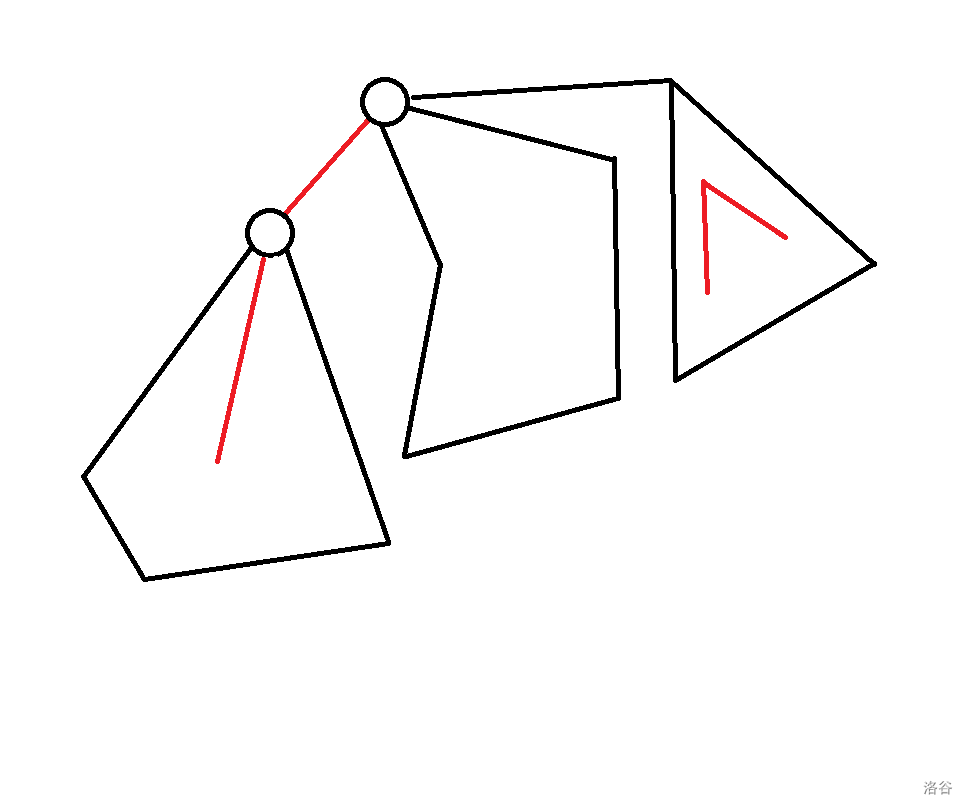
初始化的问题:$f_{p, 0}$,$f_{p, 2}$,$f_{p, 3}$ 设为 $deg_p$,即只切掉节点 $p$;$f_{p, 1}$ 设为 $1$,即不切。
~~好了完了(~~
code:
```cpp
#include <iostream>
#include <cstdio>
const int BUFFER_SIZE = 1 << 20;
char rb[BUFFER_SIZE], *rp = rb, *rt = rb;
inline char read_char() {
return rp == rt ? (rt = rb + fread(rb, 1, BUFFER_SIZE, stdin), rp = rb, *rp++) : *rp++;
}
inline int read_int() {
int x = 0;
char ch = read_char(), flag = 0;
while (ch != '-' && (ch < '0' || ch > '9')) {
ch = read_char();
}
if (ch == '-') {
flag = 1;
ch = read_char();
}
for (x = 0; ch >= '0' && ch <= '9'; ch = read_char()) {
x = x * 10 + (ch - '0');
}
return flag ? -x : x;
}
const int nn = 1e5 + 5;
int T, n, x, ans;
int cnt = 0, last[nn], prev[nn << 1], to[nn << 1];
inline void addedge(int p, int q) {
++cnt;
prev[cnt] = last[p];
last[p] = cnt;
to[cnt] = q;
}
inline void change(int &a, const int b) { a = a > b ? a : b; }
int deg[nn], f[nn][4];
void dp(int p, int father) {
f[p][0] = f[p][2] = f[p][3] = deg[p];
f[p][1] = 1;
int ret = 0;
for (int i = last[p], q; i; i = prev[i]) {
if ((q = to[i]) != father) {
dp(q, p);
change(ans, f[p][3] + f[q][0] - (p == 1));
change(ans, f[p][0] + f[q][3] - (p == 1));
change(ans, f[p][1] + f[q][2]);
change(ans, f[p][1] + f[q][1] - 1);
change(ans, f[p][2] + f[q][1] - (p == 1));
change(ans, f[p][2] + f[q][2] - (p == 1));
change(f[p][1], f[q][1]);
change(f[p][1], f[q][2] + 1);
change(f[p][3], f[p][0] + f[q][2] - 1);
change(f[p][3], f[p][0] + f[q][1] - 1);
change(f[p][3], f[p][2] + f[q][0] - 1);
change(f[p][3], f[q][3] + deg[p] - 1);
change(f[p][3], f[q][0] + deg[p] + ret - 2);
change(f[p][2], f[p][0] + f[q][0] - 1);
change(f[p][0], f[q][0] + deg[p] - 1);
change(ret, f[q][1]);
change(ret, f[q][2]);
}
}
}
void solve() {
n = read_int();
for (int i = 1; i <= x; ++i) { read_int(); read_int(); }
for (int i = 2, p, q; i <= n; ++i) {
++deg[p = read_int()];
++deg[q = read_int()];
addedge(p, q);
addedge(q, p);
--deg[i];
}
dp(1, 0);
printf("%d\n", ans);
ans = cnt = 0;
for (int i = 1; i <= n; ++i) last[i] = deg[i] = 0;
}
int main() {
T = read_int(); x = read_int();
while (T--) solve();
}
```