周期、Border、回文的部分定理证明与应用

Swirl · 2025-11-15 20:08:15 · 算法·理论

jzp 讲过两遍，匆匆来整理。

\bf{-1.} 约定

（有些需要特殊说明并证明的放在后面说）

• 没有特殊说明或明显的区分，所有大写字母均代表字符串。记 |S| 为字符串 S 的长度。
• 记 \text{Pre}(S, x) 为 S 长度为 x 的前缀，\text{Suf} 同理。
• 记 \text{LCP}(S, T) 为 S 和 T 的最长公共前缀，\text{LCS} 同理。
• 说一个 p \lt |S| 为 S 的周期，即 \forall i + p \le |S|, S_i = S_{i + p}。
• 说一个 p \lt |S| 为 S 的循环节，即 p 为 S 的周期且 p \mid |S|。
• 说一个 b \lt |S| 为 S 的 \bf{Border}，即 \text{Pre}(S, b) = \text{Suf}(S, b)。
• 记 \text{Per}(S) 为 S 的最短周期长度，周期长度集合为 P(S)。
• 记 \text{Bor}(S) 为 S 的最长 \bf{Border} 长度，\bf{Border} 长度集合为 B(S)。
• 有部分长度作为字符串书写，视为该串的前缀或原字符串。
• 记 S(l, r) 为 S 的从 l 到 r 的子串。

\bf{0.} \bf{Period}

• 描述：\forall x \in P(x), |S|-x \in B(x)，反之亦然。
• 证明：如图，略。

\bf{0/2.} \bf{Period} 与 \bf{LCP}

• 描述：p \in P(S), \text{LCP}\left(S, \text{Suf}(S, p)\right) = |S| - p。
• 证明：画图把 S 拆成若干个 p 并剩下一部分，略。

\bf{0/3/0.} \bf{WPL} 弱周期引理 ※

• 描述：若 p, q \in P(S) 且 p + q \le |S|，则 \gcd(p, q) \in P(S)。

• 证明：

  思考 \gcd 的计算方式，可以通过辗转相除法（更向减损）计算。

  那么可以考虑把 \gcd(p, q) \in P(S) 改进成 p - q \in P(S)（设 p > q），最后再用数学归纳法证明。

  则根据周期定义 S_i = S_{i + p} = S_{i + p - q}，但这并不够，因为有可能发生 i + p \gt |S| 的情况。

  所以还要考虑到 S_i = S_{i - q} = S_{i + p - q}。

  所以说 p - q \in P(S), p + q \le |S|。

  那么 \gcd(p, q) \in P(S)。\square

往后大部分证明都需要用到 \bf{WPL}，还有一个 \bf{PL}，但是没有那么重要，毕竟扩大了部分范围没有太大的作用。

\bf{0/3/\frac{1}{2}.} 推论 1

• 描述：若 p \in P(S), p \le |S| - \text{Per}(S)，则 \text{Per}(S) \mid p。

• 证明：

  令 n = |S|, \text{per} = \text{Per}(S)。

  则：

  p + \text{per} \le n - \text{per} + \text{per} = n

  根据 \bf{WPL}，p + \text{per} \le n 且 p, \text{per} \in P(S)，则 \gcd(p, \text{per}) \in P(S)。

  根据 \gcd 的定义，\gcd(p, \text{per}) \ge \text{per}；又 \text{per} 为 S 的最小周期，\gcd(p, \text{per}) \le \text{per}。

  则 \gcd(p, \text{per}) = \text{per}，即 \text{per} \mid p 。

  \text{Per}(S) \mid p $。$\square

\bf{0/3/1.} \bf{PL} 强周期引理 *

• 描述：若 p, q \in P(S) 且 p + q - \gcd(p, q) \le |S|，则 \gcd(p, q) \in P(S)。
• 证明：略，很复杂很没用。

\bf{0/4.} 循环节

• 描述：存在循环节当且仅当 \text{Per}(S) 为循环节。

• 证明：虽然很显然但是。

  令 n = |S|，q = \text{Per}(S)。

  • 充分性：若 q \mid n，则 q 为循环节，故 S 有循环节（废话）。

  • 必要性：若 S 有循环节，则存在 p \in P(S) 满足 p \mid n。因为 p < n，所以 p \le \frac{n}{2}。

    又 q = \text{Per}(S)，q \le p。

    n - q \ge n - p \ge n - \frac{n}{2} = \frac{n}{2} \ge p

    则 p \le n - q，根据 \bf{0/3/\frac{1}{2}} 中证明的结论，有 q \mid p。

    又 p \mid n，则 q \mid n，则 \text{Per}(S) 为循环节。

  \square

\bf{1.} \bf{Border}

\bf{1/0/0.} 传递性

• 描述：\forall p \in B(S),q \in B(p)，则 q \in B(S)，即 \bf{Border} 的 \bf{Border} 是原串的 \bf{Border}。
• 证明：

\bf{1/0/\frac{1}{2}}. 推论 1

• 描述：B(S) = B(\text{Bor}(S)) \cup \{\text{Bor}(S)\}。
• 证明：根据传递性。
• 引申：S 所有 \bf{Border} 形成一个树状结构，即失配树。

\bf{1/1/0.} \bf{Border} 等差数列性质 ※

• 描述：P = \left\{k \mid k \in B(S) \wedge k \ge \left \lceil \frac{|S|}{2} \right \rceil\right\}，P 构成一个公差 d = \text{Per}(S)。

• 证明：

  设字符串 S 的长度为 n，最小周期为 d = \text{Per}(S)。

  对于任意 k \in P，由边界定义，S[1..k] = S[n-k+1..n]。根据 \bf{0/1}，p = n - k 是 S 的一个周期，即 p \in P(S)。由于 k \ge \lceil n/2 \rceil，有：

  p = n - k \le n - \left \lceil \frac{n}{2} \right \rceil = \left \lfloor \frac{n}{2} \right \rfloor

  由于 d 是 S 的最小周期，有 d \le p、p \le \lfloor n/2 \rfloor，可得：

  p \le \left \lfloor \frac{n}{2} \right \rfloor \le n - d

  其中 n - d \ge \lceil n/2 \rceil 是因为 d \le \lfloor n/2 \rfloor（若 d > \lfloor n/2 \rfloor，则 p < d，与 d 是最小周期矛盾）。

  因此，p \le n - d。根据推论 \bf{0/3/\frac{1}{2}}，若 p \in P(S) 且 p \le n - d，则 d \mid p。

  故存在整数 m \ge 1 使得 p = m \times d。对应地，

  k = n - p = n - m \times d

  条件 k \ge \lceil n/2 \rceil 等价于：

  n - m \times d \ge \left \lceil \frac{n}{2} \right \rceil \iff m \times d \le n - \left \lceil \frac{n}{2} \right \rceil = \left \lfloor \frac{n}{2} \right \rfloor

  令 M = \left\lfloor \frac{\lfloor n/2 \rfloor}{d} \right\rfloor，则 m \in [1, M]。

  考虑 k = n 的情况：k = n 总是边界（因为 S[1..n] = S[1..n])，且 n \ge \lceil n/2 \rceil，故 n \in P。对应 m = 0（即 p = 0，显然 d \mid 0）。因此，P 包含 k = n - m \times d 对于 m = 0, 1, \dots, M。

  由于 d 是 S 的周期，对于 m = 0, 1, \dots, M，有 m \times d \le \lfloor n/2 \rfloor \le n，故 p = m \times d 是 S 的周期。

  根据引理 \bf{0/1}，k = n - p = n - m \times d 是边界。

  且 k \ge n - M \times d \ge n - \lfloor n/2 \rfloor = \lceil n/2 \rceil，故这些 k 均属于 P。

  因此，集合 P 可表示为：

  P = \{ n - m \times d \mid m = 0, 1, \dots, M \}

  这是一个公差为 d 的等差数列（按递减顺序排列，连续项之差为 d）。\square

\bf{1/1/\frac{1}{3}.} 双串 \bf{Border} & 推论 1

• 描述：令 \text{PS}(S, T) = \{k \mid \text{Pre}(S, k) = \text{Suf}(T, k)\}，\text{LPS}(S, T) = \left\{ k \in \text{PS}(S, T) \mid k \ge \left \lceil \frac{n}{2} \right \rceil \right\}，则 \text{LPS} 等差。

• 证明：

  若 \text{LPS}(S, T) = \emptyset，则结论平凡成立。下设 \text{LPS}(S, T) \neq \emptyset，令 M = \max(\text{LPS}(S, T))。

  由 M \in \text{LPS}(S, T)，\text{Pre}(S, M) = \text{Suf}(T, M)。

  记 U = \text{Pre}(S, M)，则 |U| = M，且由上式得 U = \text{Suf}(T, M)。

  设 \delta 为 U 的最小周期，即 \delta = \text{Per}(U)。

  任取 k \in \text{LPS}(S, T) 且 k < M。由 k \in \text{LPS}(S, T)，有 \text{Pre}(S, k) = \text{Suf}(T, k)。

  结合 U = \text{Pre}(S, M) 和 U = \text{Suf}(T, M)，可得 U[1..k] = U[M-k+1..M]。

  这意味着 p = M - k 是 U 的一个周期。事实上，对任意 i \in [1, M-p]（即 i \in [1, k]），有 U[i] = U[i+p]。

  故 p \in P(U)。

  由于 k \ge \lceil n/2 \rceil 且 M \le n，有：

  p = M - k \le M - \lceil n/2 \rceil \le n - \lceil n/2 \rceil = \lfloor n/2 \rfloor.

  考虑 \text{LPS}(S, T) 中除 M 外的最小元 m，则 m \ge \lceil n/2 \rceil，且 p' = M - m 是 U 的周期，故：

  \delta \le p' \le M - \lceil n/2 \rceil \le \lfloor n/2 \rfloor \le \lceil n/2 \rceil

  因此，对任意 k \in \text{LPS}(S, T)，有 k \ge \lceil n/2 \rceil \ge \delta。特别地，对 k < M，有：

  p + \delta = (M - k) + \delta \le (M - \delta) + \delta = M.

  由弱周期引理（WPL），p 和 \delta 是 U 的周期且 p + \delta \le |U| = M，故 \gcd(p, \delta) \in P(U)。但 \delta 是 U 的最小周期，所以 \gcd(p, \delta) = \delta，即 \delta \mid p。因此：

  \delta \mid (M - k) \Rightarrow k \equiv M \pmod{\delta}.

  这表明 \text{LPS}(S, T) 中所有元素均模 \delta 同余于 M，故 \text{LPS}(S, T) 是公差为 \delta 的等差数列（可能为单点集）。

  综上，\text{LPS}(S, T) 为等差数列。\square

\bf{1/1/\frac{2}{3}.} 推论 2

• 描述：B(S) 可以构成 \mathcal{O}(\log |S|) 个等差数列。

• 证明：

  不会证，参考 AI 的。

  定义序列 \{L_i\} 如下：

  • 令 L_0 = n。

  • 对于 i \geq 0，若 L_i > 0，则：

    • 设 d_i = \text{Per}(\text{Pre}(S, L_i))，即前缀 \text{Pre}(S, L_i) 的最小周期。

    • 根据边界等差数列性质，集合

      A_i = \{ L_i - j \times d_i \mid j = 0, 1, \dots, m_i \}

      是 B(S) 的子集，其中 m_i 是最大整数使得 L_i - m_i \cdot d_i \in B(S) 且 L_i - m_i \cdot d_i > L_i/2。

    • 令 L_{i+1} = L_i - m_i \cdot d_i。

  由构造可知，A_i 中的边界均满足 L_i/2 < k \leq L_i，且 A_i 是公差为 d_i 的等差数列。
  又因为 L_{i+1} \leq L_i/2，序列 \{L_i\} 严格递减，且 L_{i+1} \leq L_i/2，故经过 \mathcal{O}(\log n) 步后 L_i 变为 0。

  • 覆盖性：任意 k \in B(S) 必属于某个 A_i。若 k > L_1，则 k \in A_0；

    否则，存在 i 使得 L_{i+1} < k \leq L_i，此时 k \in A_i。

  • 不相交性：对于 i < j，A_i 中的边界均大于 L_i/2 \geq L_{i+1}，而 A_j 中的边界均 \leq L_j \leq L_{i+1}，故 A_i \cap A_j = \emptyset。

  因此，\{A_i\} 是 B(S) 的一个划分，且共有 \mathcal{O}(\log n) 个等差数列。

  字符串 S 的边界集合 B(S) 可划分为 \mathcal{O}(\log |S|) 个等差数列。\square

\bf{1/2.} 大肠包小肠

• 描述：\bf{Border} 在 S 中两次匹配的位置的重叠部分是另一个 \bf{Border}。
• 证明：

\bf{1/3.} 匹配等差

• 描述：两个字符串 S、T，若 |S| \ge \left \lceil \frac{|T|}{2} \right \rceil，则 S 在 T 中的匹配位置等差，d = \text{Per}(S)。

• 证明：哦我会了不用磕头了。

  设 S 在 T 中出现的位置分别为 p_1, p_2, \cdots, p_k。

  若 k \le 2，则结论平凡成立，下设 k \ge 3。

  对于任意的 i < j，有：

  p_j - p_i \le |T| - |S| \le \left \lceil \frac{|T|}{2} \right \rceil \le |S|

  所以出现位置重叠，\text{Pre}(S, |S| - p_j + p_i) = \text{Suf}(S, |S| - p_j + p_i + 1)。

  则 p_j - p_i \in P(S)。

  设 d_i = p_{i + 1} - p_i，故 \forall i \in [1, k - 1], d_i \in P(S)。

  则 d_1 + d_2 = p_3 - p_1 \le |S|，根据 \bf{WPL}，\gcd(d_1, d_2) \in P(S)，\text{Per}(S) \le \gcd(d_1, d_2) \le d_1, d_2。

  设 d = \text{Per}(S)，若 d_1 > d，则存在 p > 1 使得 d_1 = pd。因为 S 有周期 d，所以 p_1 + d 同时也在数列 p 中。但这与 p_2 = p_1 + pd 与 p_1 相邻矛盾，则 d_1 \le d。

  又 d = \text{Per}(S)，所以 d_1 = d。

  同理可得 d_2, d_3, \cdots, d_{k - 1} 均为 d，p 为等差数列。\square

\bf{2.} \bf{KMP} 算法

主要解决字符串匹配问题，考虑失配之后的次优位置 \pi 函数。

所以说 \pi 函数的定义就呼之欲出了，即 \pi_i = \text{Bor}(\text{Pre(S, i)})。

如何转移，思考 \pi \text{-box} 的位置。

我们发现，\text{Bor}(\text{Pre}(S, i)) - \text{Bor}(\text{Pre}(S, i - 1)) \le 1，也就是说 \pi_i \le \pi_{i - 1} + 1，这可以势能分析，\pi 总共最多会减小 \mathcal{O}(n) 次，所以通过确定上界不断减小时间复杂度是正确的。

代码不放了。

\bf{2/0}. 延申

• 广义 \bf{KMP}：听同机房巨佬讲的高端东西，只要满足所有 [l, r] \subseteq [1, n]，均有 S(1, n) = T(1, n) \implies S(l, r) = T(l, r)，则都可以用 \bf{KMP} 判等。

  • P4696 - 洛谷

  题目即重新定义了一个序列的相等，可以使用广义 \bf{KMP}。

  将序列重排，重新定义相等为前驱后继大小关系分别相同。

  然后跑 \bf{KMP} 即可，注意判等的条件在计算 \pi 和统计答案时不一样。

\bf{3.} \bf{Manacher} 算法

主要解决最长回文子串问题，考虑对于每个点求其作为回文中心的最长回文子串长度 d。

由于 i 为中心的回文所在镜像 i^{`} 亦是回文中心，两端是相同的。

找找 p\text{-box}。

假设当前我们已经求出 p_1, p_2, \cdots, p_{i - 1}，那么我们可以确定一个 C 和一个 R_{\max}，使得在 j = C < i 时，R_{\max} = p_j + j 最大。

那么由于对称性，R_{\max} 及其左边都是确定了的。

• 如果 i \gt R_{\max}，没有别的方法，直接用暴力确定 p_i。

• 否则，又分为两种情况：

  • 若 \bar i 的左端在 \bar{R_{\max}} 右侧，那么以 p_{\bar{i}} 为基础对 i 进行中心扩展。
  • 否则，以 R_{\max} - i 为基础进行中心扩展，图不想画了，自行脑补。

代码仍然不写。

\bf{3/0.} 延申

• 说说 \bf{Manacher} 复杂度的正确性。
  • 在 i \gt R_{\max} 的情况下，虽然需要暴力，但是 i 每增加 1，R_{\max} 也会同时加上 1，而 R 上界是 n，所以正确。
  • 在 i \le R_{\max} 的情况下，直接能 \mathcal{O}(1) 确定，不用管。
• - 对于每个点记 $l_i$ 为以 $i$ 为右端点的最长回文子串长度，我们考虑找 $l\text{-box}$。 - 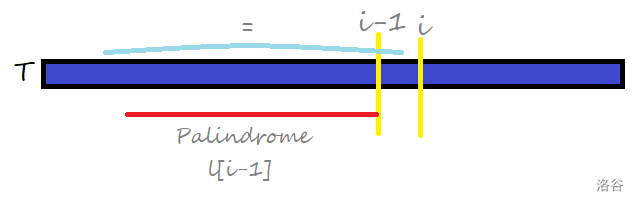 - 我们发现，$l_i$ 的上界是 $l_{i - 1} + 2$，这就是 $l\text{-box}$。 - 所以说可以哈希直接判，复杂度均摊 $\mathcal{O}(n)$。
• 虽然这不是最长回文子串的更常用的解法，因为 \bf{Manacher} 有更多的延申且本解法涉及哈希有可能会冲突，但是我认为这作为最长回文子串这单一问题的解法挺好的。