数论基础知识及拓展
wenqinghua1001
·
·
算法·理论
教学内容:
- 整除的性质和特征
- 质数与合数的性质
- 公约数与公倍数
- 同余的性质
- 数论分块
教学难点:
- 质数与合数的性质
- 同余的性质
- 数论分块的性质和问题的转化
- 拓展欧几里得和唯一分解定理
- 欧拉函数与同余四则运算
- 逆元与矩阵快速幂
1. 整除性质和特征
1.1 整除的定义\
1.2 整除的性质\
1.3 整除的特征
1.1 整除的定义
设 a,b 是整数,b \ne 0,如果存在整数 c,使得 a=b \times c 成立,则称 a 被 b 整除,a 是 b 的倍数,b 是 a 的约数(因数或除数),并且使用记号 b \mid a。
1.1.1 约数的正负
约数有正约数和负约数,我们只讨论正约数。
1.1.2 约数的有限性
对于任意非零整数 a,约数的个数是有限的。
1.1.3 约数总有一
### 1.1.4 零不作约数
$0$ 不能作为约数,**但 $0$ 是任何非零整数的倍数**,对任何非零整数 $a$,总有 $a \mid 0$。
## 1.2 整除的性质
以下 $a$,$b$,$c$ 均为整数。
### 1.2.1 性质一
如果 $c \mid a$,$c \mid b$,那么 $c \mid (a \pm b)$。
### 1.2.2 性质二
如果 $(b \times c) \mid a$,那么 $b \mid a$,$c \mid a$。
### 1.2.3 性质三
如果 $b \mid a$,那么 $b \mid (a \times c)$。
### 1.2.4 性质四
如果 $b \mid a$,$c \mid a$,且 $b \perp c$,那么 $(b \times c) \mid a$。
证明:\
唯一分解定理:$s={P_1}^{C_1} \times {P_2}^{C_2} \times \cdots \times {P_{k-1}}^{C_{k-1}} \times {P_k}^{C_k}$,$P_i$ 是质数且 $C_i \ge 1$。将 ${P_1}^{C_1} \times {P_2}^{C_2} \times \cdots \times {P_{k-1}}^{C_{k-1}} \times {P_k}^{C_k}$ 分成三个集合,无重复,称第一个集合为 $A$,第二个集合为 $B$,无论怎么分都满足 $(A \times B) \mid s$。
### 1.2.5 性质五
如果 $c \mid b$,$b \mid a$,那么 $c \mid a$。
### 1.2.6 性质六
$n$ 个连续整数中,有且只有一个是 $n$ 的倍数。
### 1.2.7 性质七
任何 $n$ 个连续的整数之积一定是 $n!$ 的倍数。
用 1.2.6 的性质可以证明,$n$ 个连续整数中,有且只有一个是 $n$ 的倍数。以此推出有且只有一个是 $n-1$ 的倍数,有且只有一个是 $n-2$ 的倍数,一直到 $1$。所以,$n$ 个连续的整数中,每个数字都有一个(可能有多个)在 $1$ 到 $n$ 里的约数。
例如:$n=5$,数列是 $6,7,8,9,10$,乘积是 $6 \times 7 \times 8 \times 9 \times 10$,$n!=5!=1 \times 2 \times 3 \times 4 \times 5$。满足 $1 \mid 7$,$2 \mid 6$,$3 \mid 9$,$4 \mid 8$,$5 \mid 10$,所以 $6 \times 7 \times 8 \times 9 \times 10$ 是 $n!$ 的倍数。
## 1.3 整除的特征
### 1.3.1 二的倍数
$2$ 的倍数的特征:个位数字是 $0,2,4,6,8$ 其中一个的整数。
### 1.3.2 三、九的倍数
$3$(或 $9$)的倍数的特征:各个数位上的数之和能被 $3$(或 $9$)整除。
### 1.3.3 四、二十五的倍数
$4$(或 $25$)的倍数的特征:末两位能被 $4$(或 $25$)整除。
### 1.3.4 五的倍数
$5$ 的倍数的特征:个位是 $0$ 或 $5$。
### 1.3.5 六的倍数
$6$ 的倍数的特征:同时满足 1.3.1 和 1.3.2。例如 $1145141919810$ 是 $6$ 的倍数。
### 1.3.6 八、一百二十五的倍数
$8$(或 $125$)的倍数的特征:末三位能被 $8$(或 $125$)整除。
### 1.3.7 十一的倍数
$11$ 的倍数的特征:奇数位上的数之和与偶数位上的数之和的差是 $11$ 的倍数。方法二为 1.3.8。
### 1.3.8 七、十一(第二种方法)、十三的倍数
$7$($11$ 或 $13$)的倍数的特征:末三位与末三位以前的数字所组成的数字之差能被 $7$($11$ 或 $13$)整除。
# 2. 质数与合数的性质
2.1 质数和合数的定义\
2.2 质数和合数的性质\
2.3 有趣的数\
2.4 线性筛
## 2.1 质数和合数的定义
### 2.1.1 特殊的数
$0$ 和 $1$ 既不是质数,也不是合数。
### 2.1.2 质数
质数(素数)是大于 $1$ 的整数,除了 $1$ 和它本身外,没有其它约数的数。
### 2.1.3 合数
合数是大于 $1$ 的整数,除了 $1$ 和它本身外,还有其它约数的数。
### 2.1.4 判断质数
#### 2.1.4.1 暴力筛
```cpp
bool is_prime(int x){
if(x<2) return false;
int l=(int)sqrt(x);
for(int i=2;i<=l;i++){
if(x%i==0)
return false;
}
return true;
}
```
#### 2.1.4.2 埃氏筛
```cpp
int p[N+5];
void primes(){
int l=(int)sqrt(N);
for(int i=2;i<=l;i++){
if(p[i]==0){
for(int j=i*i;j<=N;j+=i)
p[j]=1;
}
}
}
```
## 2.2 质数和合数的性质
### 2.2.1 质因子范围
如果 $n$ 是合数,则 $n$ 必有一个质因子 $x$,满足 $2 \le x \le \sqrt{n}$。但满足 $x \ge \sqrt{n}$ 的 $x$ 最多只有一个。
### 2.2.2 中国唯一分解定理
中国唯一分解定理又叫算术基本定理。任何大于 $1$ 的整数 $a$,都可以分解成有限个质数的乘积:
$$
a=p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}=\prod_{i=1}^{k}p_i^{c_i}
$$
$p_i$ 为质数,上式叫做整数 $a$ 的标准分解式。
### 2.2.3 分解质因数
```cpp
int a[N],cnt=0;
void fenjie(int n){
for(int i=2;i<=sqrt(n);i++){
while(n%i==0){
n/=i;
a[++cnt]=i;
n=n/i;
}
}
if(n>1) a[++cnt]=n;
}
```
### 2.2.4 正因数个数
$$
a=p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}=\prod_{i=1}^{k}p_i^{c_i}
$$
若 $a$ 的标准分解式为上式,$a$ 的正因数的个数 $f(a)$ 为:
$$
f(a)=(c_1+1) \times (c_2+1) \times \cdots \times (c_k+1)=\prod_{i=1}^{k}c_i+1
$$
### 2.2.5 正因数之和
$$
a=p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}=\prod_{i=1}^{k}p_i^{c_i}
$$
若 $a$ 的标准分解式为上式,$a$ 的正因数之和 $f(a)$ 为:
\begin{aligned}
f(a) &= ({p_1}^0+{p_1}^1+ \cdots +{p_1}^{c_1}) \times ({p_2}^0+{p_2}^1+ \cdots +{p_2}^{c_2}) \times \cdots \times ({p_k}^0+ \cdots+{p_k}^{ck}) \
&=\sum{j=0}^{c_1}{p1}^j \times \sum{j=0}^{c_2}{p2}^j \times \cdots \times \sum{j=0}^{c_k}{pk}^j \
&=\prod{i=1}^{k} \sum_{j=0}^{c_i} {p_i}^j
\end{aligned}
## 2.3 有趣的数
### 2.3.1 哥德巴赫猜想
#### 2.3.1.1 哥德巴赫猜想一
任意大于 $5$ 的整数都可以写成三个质数的和。
#### 2.3.1.2 哥德巴赫猜想二
任意大于 $2$ 的偶数都可以写成两个质数的和。
#### 2.3.1.3 哥德巴赫猜想三
随意取一个正整数 $x$,根据以下规则调整 $x$ 的值。
- 如果 $x$ 是偶数且 $x \ne 1$,那么将 $x=x \div 2$。
- 如果 $x$ 是奇数且 $x \ne 1$,那么将 $x=x \times 3 + 1$。
最终无论如何,都会满足 $x=1$。
### 2.3.2 孪生素数
数学上把相差为 $2$ 的两个质数叫做“孪生素数”。
## 2.4 线性筛
### 2.4.1 线性筛定义
线性筛,又叫**欧拉筛**,顾名思义,时间复杂度是 $O(n)$ 的。其原理是每个数都保证只被其最小的质因子筛去。
对于**积性函数** $f$,线性筛可以在线性时间复杂度内,计算出 $f(1) \sim f(N)$ 的值。
**积性函数**:所有互质的整数 $a$ 和 $b$ 有 $f(a \times b)=f(a) \times f(b)$ 的数论函数。
```cpp
int p[N],b[N],pn=0;
void Prime(int n){
for(int i=2;i<=n;i++){
if(b[i]==0) p[++pn]=i;
for(int j=0,k;j<pn&&(k=i*p[j])<=n;j++){
b[k]=1;
if(i%p[j]==0)
break;
}
}
}
```
### 2.4.2 线性筛例题
#### 2.4.2.1 例题一:约数个数
$$
f(a)=(c_1+1) \times (c_2+1) \times \cdots \times (c_k+1)=\prod_{i=1}^{k}c_i+1
$$
题目意思是要你求 $A$ 的约数个数,$Q$ 次询问($A \le 10^7$,$Q \le 10^6$),分析:
设 $a \perp b$。\
$a$ 有唯一分解式 $a={p_{a_1}}^{c_{a_1}} \times {p_{a_2}}^{c_{a_2}} \times \cdots \times {p_{a_k}}^{c_{a_k}}$。\
$b$ 有唯一分解式 $b={p_{b_1}}^{c_{b_1}} \times {p_{b_2}}^{c_{b_2}} \times \cdots \times {p_{b_k}}^{c_{b_k}}$。
已知:\
$f(a)=(c_{a_1}+1) \times (c_{a_2}+1) \times \cdots \times (c_{a_k}+1)$。\
$f(b)=(c_{b_1}+1) \times (c_{b_2}+1) \times \cdots \times (c_{b_k}+1)$。
由于 $a \perp b$,可知 $p_{a_i} \ne p_{b_j}$。
则 $f(a \times b)=((c_{a_1}+1) \times (c_{a_2}+1) \times \cdots \times (c_{a_k}+1)) \times ((c_{b_1}+1) \times (c_{b_2}+1) \times \cdots \times (c_{b_k}+1))=f(a) \times f(b)$,可知该函数是积性函数。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e7+5;
int p[N],b[N],pn=0,c1[N],num[N]={0,1};
void Prime(int n){
for(int i=2;i<=n;i++){
if(b[i]==0){
p[pn++]=i;
c1[i]=1;
num[i]=2;
}
for(int j=0,k;j<pn&&(k=i*p[j])<=n;j++){
b[k]=1;
if(i%p[j]==0){
c1[k]=c1[i]+1;
num[k]=num[i]/c1[k]*(c1[k]+1);
break;
}
else{
c1[k]=1;
num[k]=num[i]*2;
}
}
}
}
int main(){
int Q;
cin>>Q;
Prime(1e7);
while(Q--){
int A;
cin>>A;
cout<<num[A]<<endl;
}
return 0;
}
```
#### 2.4.2.2 例题二:约数和
\begin{aligned}
f(a) &= ({p_1}^0+{p_1}^1+ \cdots +{p_1}^{c_1}) \times ({p_2}^0+{p_2}^1+ \cdots +{p_2}^{c_2}) \times \cdots \times ({p_k}^0+ \cdots+{p_k}^{ck}) \
&=\sum{j=0}^{c_1}{p1}^j \times \sum{j=0}^{c_2}{p2}^j \times \cdots \times \sum{j=0}^{c_k}{pk}^j \
&=\prod{i=1}^{k} \sum_{j=0}^{c_i} {p_i}^j
\end{aligned}
题目意思是 $M$ 次询问正整数 $X$ 的约束和($X \le 10^7$,$M \le 10^6$)。
例题一“约数个数”证明过了积性函数,可以参照例题一证明来证明本题。得到结果 $f(a)=\prod_{i=1}^{k} \sum_{j=0}^{c_i} {p_i}^j$ 是积性函数,可以用欧拉筛。
```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int p[N],b[N],pn=0,s1[N],s[N]={0,1};
void Prime(int n){
for(int i=2;i<=n;i++){
if(b[i]==0){
p[pn++]=i;
s[i]=i+1;
s1[i]=1;
}
for(int j=0,k;j<pn&&(k=i*p[j])<=n;j++){
b[k]=1;
if(i%p[j]==0){
s1[k]=s1[i];
s[k]=s1[k]+p[j]*s[i];
break;
}
else{
s1[k]=s[i];
s[k]=s[i]*(p[j]+1);
}
}
}
}
signed main(){
int M;
cin>>M;
Prime(1e7);
while(M--){
int X;
cin>>X;
cout<<s[X]<<endl;
}
return 0;
}
```
# 3. 公约数与公倍数
3.1 公约数与公倍数的定义\
3.2 最大公约数和最小公倍数的关系\
3.3 更相减损术
## 3.1 公约数与公倍数的定义
**公约数**与**最大公约数**:几个数公有的约数,叫做这几个数的公约数,有限个。其中最大的一个,叫做这几个数的最大公约数。
例如:$4$ 是 $12$ 和 $16$ 的最大公约数,可以记作 $(12,16)=4$ 或 $\gcd(12,16)=4$。
**公倍数**与**最小公倍数**:几个数公有的倍数,叫做这几个数的公倍数,无限个。其中最小的一个,叫做这几个数的最小公倍数。
例如:$36$ 是 $12$ 和 $18$ 的最小公倍数,可以记作 $\begin{bmatrix} 12,18 \end{bmatrix}=36$。
**互质**:两个不同的自然数,它们只有一个公因数 $1$,则称它们互质。
$a$ 与 $b$ 互质,记为 $(a,b)=1$ 或 $\gcd(a,b)=1$ 或 $a \perp b$。
## 3.2 最大公约数和最小公倍数的关系
用 $a$ 和 $b$ 表示两个自然数。
### 3.2.1 关系一:乘积
$(a,b) \times \begin{bmatrix} a,b \end{bmatrix} = a \times b
证明:设 a=d \times x,b=d \times y,则 (a,b)=d,\begin{bmatrix} a,b \end{bmatrix}=d \times x \times y,则 (a,b) \times \begin{bmatrix} a,b \end{bmatrix} = d \times d \times x \times y= (d \times x) \times (d \times y)=a \times b。
3.2.2 关系二:大小
(a,b) \le a,b \le \begin{bmatrix} a,b \end{bmatrix}
看一眼就知道。
3.2.3 关系三:倍数关系
(a,b) \mid \begin{bmatrix} a,b \end{bmatrix}
3.2.4 关系四:加减
$(a,b) \mid (\begin{bmatrix} a,b \end{bmatrix} + (a,b))$\
$(a,b) \mid (\begin{bmatrix} a,b \end{bmatrix} - (a,b))
显而易见。
3.3 更相减损术
3.3.1 回顾辗转相除法
原理:(a,b)=(a,a \bmod b)。
int gcd1(int a,int b){
for(int c;b>0;c=a%b,a=b,b=c);
return a;
}
int gcd2(int a,int b){
if(b==0) return a;
return gcd2(b,a%b);
}
3.3.2 更相减损术的介绍与拓展
注意,更相减损术并不比辗转相除法慢,元素多的时候反而比辗转相除法快。
原理:(a,b)=(a,\lvert b-a \rvert),保证 b \ge a。
拓展:
$(a_1,a_2, \cdots ,a_{n-1} ,a_n)=\lvert (a_1,a_2-a_1, \cdots ,a_n-a_{n-1}) \rvert$,保证 $a_1 \le a_2 \le \cdots \le a_{n-1} \le a_n$。
```cpp
int gcd3(int a,int b){
while(a!=b){
if(a>b) a-=b;
else b-=a;
}
return a;
}
```
### 3.3.3 更相减损术的例题
#### 3.3.3.1 例题题面
给定两个整数数列 $x_1,x_2, \cdots ,x_{n-1},x_n$ 和 $y_1,y_2, \cdots ,y_{m-1},y_m$。对于每个 $j=1,2,\cdots,m$,计算出序列 $x_1+y_j,x_2+y_j,\cdots,x_n+y_j$ 的最大公约数。数据满足 $1 \le x_i,y_j \le 10^{18}$,$1 \le n,m \le 3 \times 10^5$。
#### 3.3.3.2 例题分析
更相减损术,先进行预处理,$g=(x_2-x_1,x_3-x_2,\cdots,x_n-x_{n-1})$。
对于每个 $j=1,2,\cdots,m$,只需输出 $(x_1+y_j,g)$ 的结果即可,时间复杂度为 $O(n \times \log(2^{18})+m \times \log(2^{18}))$。
辗转相除法时间复杂度为 $O(n \times m)$。
#### 3.3.3.3 例题代码
```cpp
#include<bits/stdc++.h>
using namespace std;
long long x[1000001];
long long y[1000001];
int main(){
long long n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&x[i]);
for(int i=1;i<=m;i++)
scanf("%lld",&y[i]);
long long g=x[2]-x[1];
for(int i=1;i<n;i++)
g=__gcd(g,x[i+1]-x[i]);
g=abs(g);
for(int j=1;j<=m;j++)
printf("%lld ",__gcd(g,x[1]+y[j]));
return 0;
}
```
# 4. 同余的性质
4.1 同余的定义\
4.2 同余的性质定理\
4.3 同余的简单练习
## 4.1 同余的定义
给定正整数 $m$,如果整数 $a$ 与 $b$ 之差被 $m$ 整除,则称 $a$ 与 $b$ 对于模 $m$ 同余,或称 $a$ 与 $b$ 同余,模 $m$,记为 $a \equiv b(\bmod \ m)$。也称 $b$ 是 $a$ 对模 $m$ 的同余。
## 4.2 同余的性质定理
模运算与四则运算有些相似,但是除法例外。其规则如下:
$(a+b) \bmod p=(a \bmod p + b \bmod p) \bmod p
(a-b) \bmod p=(a \bmod p - b \bmod p + p) \bmod p
(a \times b) \bmod p=(a \bmod p \times b \bmod p) \bmod p
a^b \bmod p=((a \bmod p)^b) \bmod p
模运算的除法:
~~先说一些废话,也是大实话。~~
$a \equiv a(\bmod \ m)$。
$a \equiv b(\bmod \ m)$,则 $b \equiv a(\bmod \ m)$。
$a \equiv b(\bmod \ m)$,$b \equiv c(\bmod \ m)$,则 $a \equiv c(\bmod \ m)$。
___
如果 $a \equiv b(\bmod \ m)$,$c \equiv d(\bmod \ m)$。
则 $a+c \equiv b+d(\bmod \ m)$,$a \times c \equiv b \times d(\bmod \ m)$。
___
如果 $a \equiv b(\bmod \ m)$,$k>0$,$k \in N$。则 $a+k \equiv b+k(\bmod \ m)$。
如果 $a \equiv b(\bmod \ m)$,$k>0$,$k \in N$。则 $a \times k \equiv b \times k(\bmod \ m)$。
如果 $a \equiv b(\bmod \ m)$,$d \mid m$,$d > 0$。则 $a \equiv b (\bmod \ d)$。
如果 $a \equiv b(\bmod \ m_i)$,$1 \le i \le k$。则 $a \equiv b (\bmod \ \begin{bmatrix} m_1,m_2,\cdots,m_k \end{bmatrix})$。
如果 $a \equiv b(\bmod \ m)$,则 $(a,m)=(b,m)$。
如果 $a \times c \equiv b \times c(\bmod \ m)$,$c \perp m$。则 $a \equiv b(\bmod \ m)$。
## 4.3 同余的简单练习

# 5. 数论分块
5.1 数论分块定义\
5.2 数论分块性质\
5.3 数论分块模版\
5.4 N 维数论分块\
5.5 数论分块例题
## 5.1 数论分块定义
数论分块也叫整除分块,是数学问题中一个优化时间复杂度的技巧,通常用于快速求解形如 $\sum_{i=1}^{n}f(i) \times g(\lfloor \frac{n}{i} \rfloor)$ 的问题。当可以在 $O(1)$ 时间复杂度内计算出 $\sum_{i=l}^{r}f(i)$ 或已经预处理出 $f$ 的前缀和时,数论分块就可以在 $O(\sqrt{n})$ 的时间内计算上述和式的值。

其原理是可以将 $\lfloor \frac{n}{i} \rfloor$ 相同的 $g(\lfloor \frac{n}{i} \rfloor)$ 函数值打包计算。
## 5.2 数论分块性质
### 5.2.1 性质一:分块数量
**问题**:
对任意的正整数 $n$,其不同商的个数不会超过多少呢?
___
**解答**:
给定 $n$,求算式 $\lfloor \frac{n}{i} \rfloor=x$ 中 $x$ 的最大数量,$i$ 和 $x$ 都为正整数。
我们分成两种情况来考虑:$i \le \sqrt{n}$ 和 $i > \sqrt{n}$。
$ i \le \sqrt{n}$ 时:
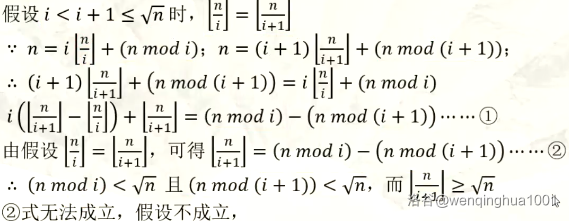
可知 $\lfloor \frac{n}{i} \rfloor$ 的值在 $1 \le i \le \sqrt{n}$ 范围内各不相同,共 $\sqrt{n}$ 个不同的值。
$ i > \sqrt{n}$ 时:
随着 $i$ 的增大 $\lfloor \frac{n}{i} \rfloor$ 的值单调不升,最大值是 $\lfloor \sqrt{n} \rfloor$,最小值为 $1$,所以不同值的个数为 $\lfloor \sqrt{n} \rfloor$。

$\sqrt{n}+\sqrt{n}=2 \times \sqrt{n}
结论:
最后,对任意的正整数 n,其不同商的个数不会超过 2 \times \sqrt{n}。
5.2.2 性质二:连续整除
性质:
**证明**:
设 $\frac{a}{b}=\lfloor \frac{a}{b} \rfloor + r$。
$$\begin{aligned}
\lfloor \frac{a}{b \times c} \rfloor &= \lfloor \frac{a}{b} \times \frac{1}{c}\rfloor\\
&= \lfloor \frac{1}{c} \times (\lfloor \frac{a}{b} \rfloor + r) \rfloor\\
&= \lfloor \frac{\lfloor \frac{a}{b} \rfloor}{c}+\frac{r}{c} \rfloor\\
&= \lfloor \frac{\lfloor \frac{a}{b} \rfloor}{c} \rfloor
\end{aligned}$$
### 5.2.3 性质三:分块边界


## 5.3 数论分块模版
### 5.3.1 例题:商之和(模版)
求 $\sum_{i=1}^{n}\lfloor \frac{n}{i}\rfloor$,$1 \le n \le 2^{32}$。
代码:
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll DivBlock(ll n){
ll res=0;
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l);
res=res+n/l*(r-l+1);
}
return res;
}
int main(){
ll n;
scanf("%lld",&n);
printf("%lld\n",DivBlock(n));
return 0;
}
```
## 5.4 N 维数论分块
一维数论分块我们已经讨论过了,接下来我们讨论二维数论分块。
二维数论分块可以处理形如 $\sum_{i=1}^{\min(n,m)}f(\lfloor \frac{n}{i} \rfloor) \times g(\lfloor \frac{m}{i} \rfloor)$ 的问题。

其中每块右端点下标,由一维时的 $r=n \div (n \div l)$ 改为 $r=\min(\frac{n}{\frac{n}{l}},\frac{m}{\frac{m}{l}})$。
二维以上同理。
## 5.5 数论分块例题
### 5.5.1 例题一:约数个数和
计算 $1 \sim n$ 内所有整数约数个数之和,$1 \le n \le 2^{32}$。
$\begin{bmatrix} 1,n \end{bmatrix}$ 里有约束 $i$ 的数的个数是 $\lfloor \frac{n}{i} \rfloor$ 个。
所以 $ans=\sum_{i=1}^{n}\lfloor \frac{n}{i} \rfloor$。
于是就可以用数论分块处理了,时间复杂度为 $O(\sqrt{n})$,代码同“商之和”。
### 5.5.2 例题二:约束和续
计算 $x \sim y$ 内所有整数的约数之和的和,$1 \le x \le y \le 2 \times 10^9$。
先思考 $S(n)$,表示 $1 \sim n$ 以内所有数的约束和的和。换一个维度思考,$i$ 作为约数的贡献有几次,显然是 $\lfloor \frac{n}{i} \rfloor$ 次。可以给出公式 $\sum_{i=1}^{n}(\lfloor \frac{n}{i} \rfloor\times i)$。
$$
\sum_{i=l}^{r}(\lfloor \frac{n}{i} \rfloor\times i)=\lfloor \frac{n}{l} \rfloor \times \sum_{i=l}^{r}i=\lfloor \frac{n}{l} \rfloor \times (l+r) \times (r-l+1) \div 2
$$
输出前缀和。
代码:
```cpp
#include<cstdio>
using namespace std;
typedef long long ll;
ll sum(int n){
if(n<=1) return n;
ll ans=0;
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l);
ans+=(n/l)*(l+r)*(r-l+1)/2;
}
return ans;
}
int main(){
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",sum(y)-sum(x-1));
return 0;
}
```
### 5.5.3 例题三:阶乘质因数分解
将 $n!$ 分解成若干个质数的积,$n \le 10^7$。
分析:
$$
\text{设} n!={p_1}^{r_1} \times {p_2}^{r_2} \times \cdots \times {p_k}^{r_k} \text{,则} r_i=\sum_{i=1}^{p^i<n}\lfloor \frac{n}{p^i} \rfloor \text{。}
$$
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
long long d[10000005],id=0;
long long r[10000005];
void prime(long long n){
r[1]=1;
for(long long i=2;i<=n;i++){
if(r[i]==0){
d[++id]=i;
for(long long j=i*i;j<=n;j+=i)
r[j]=1;
}
}
}
int main(){
long long n;
cin>>n;
prime(n);
for(long long i=1;i<=id;i++){
long long ans=0;
long long m=n;
while(m>1){
m/=d[i];
ans+=m;
}
if(ans>0) cout<<ans<<" ";
}
return 0;
}
```
### 5.5.4 例题四:组合数因子个数
求组合数 $C_n^k$ 的不同因子的个数,$2 \le k \le n \le 431$。
运用数论分块和中国唯一剩余定理,很简单地可以解出这题。埃氏筛时在 $c_i$ 中记录 $i$ 的最小质因子,$C$ 函数用于计算组合数约数个数,这种解法比较巧妙。
代码:
```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=450;
int p[N],pn,c[N];
void Prime(){
int m=23;
for(int i=2;i<=m;i++){
if(c[i]==0){
for(int j=i*i;j<N;j+=i){
if(c[j])
continue;
else
c[j]=i;
}
}
}
for(int i=2;i<N;i++)
if(c[i]==0)
p[pn++]=i;
}
int b[N];
int C(int n,int k){
memset(b,0,sizeof b);
for(int i=2;i<=n;i++)
b[i]++;
for(int i=2;i<=k;i++)
b[i]--;
for(int i=2;i<=n-k;i++)
b[i]--;
for(int i=n;i>1;i--){
if(c[i]>0){
b[c[i]]+=b[i];
b[i/c[i]]+=b[i];
b[i]=0;
}
}
int ans=1;
for(int i=0;i<pn;i++)
ans*=b[p[i]]+1;
return ans;
}
signed main(){
int p;
cin>>p;
Prime();
while(p--){
int n,k;
cin>>n>>k;
cout<<C(n,k)<<endl;
}
return 0;
}
```
### 5.5.5 例题五:素数密度
给定区间 $\begin{bmatrix} L,R \end{bmatrix}$,请计算区间中素数的个数。$2 \le L \le R \le 2147483647$,$R-L \le 10^6$。一道欧拉筛加数论分块。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1e6+1;
ll l,r;
int prime[maxn],cnt,ans;
bool vis[maxn];
void aprime(){
for(register int i=2;i<=50000;++i){
if(!vis[i])prime[++cnt]=i;
for(register int j=1;i*prime[j]<=50000;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
cin>>l>>r;
l=l==1?2:l;
aprime();
memset(vis,0,sizeof(vis));
for(register int i=1;i<=cnt;++i){
ll p=prime[i],start=(l+p-1)/p*p>2*p?(l+p-1)/p*p:2*p;
for(register ll int j=start;j<=r;j+=p)
vis[j-l+1]=1;
}
for(register int i=1;i<=r-l+1;++i)
if(!vis[i]) ans++;
cout<<ans;
return 0;
}
```
### 5.5.6 例题六:余数和
给出正整数 $n$ 和 $k$,请计算下式的值,$1 \le n,k \le 10^9$。
$$
G(n,k)=\sum_{i=1}^n k \bmod i
$$
分析:这是一道数论分块题目,根据式子 $\sum_{i=l}^{r}(\lfloor \frac{n}{i} \rfloor\times i)=\lfloor \frac{n}{l} \rfloor \times \sum_{i=l}^{r}i=\lfloor \frac{n}{l} \rfloor \times (l+r) \times (r-l+1) \div 2$,可以得出答案,用 $res$ 累加,最后输出 $n \times k - res$。
代码:
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll qh(ll n,ll k){
ll res=0;
for(ll l=1,r;l<=n;l=r+1){
if(k/l!=0)
r=min(k/(k/l),n);
else
r=n;
res+=(k/l)*(l+r)*(r-l+1)/2;
}
return n*k-res;
}
int main(){
ll n,k;
scanf("%lld%lld",&n,&k);
printf("%lld\n",qh(n,k));
return 0;
}
```