题解 P6750 【『MdOI R3』Pekka Bridge Spam】
JohnVictor
·
·
题解
放上官方题解,自认为这题还是不错的,主要是对于结构的观察而不是推式子。
性质 1
将这个图分成 nm 个 2 \times 2 个正方形,那么每个正方形中恰好有一个 1 \times 2。
证明:称 S 为所有被 1 \times 2 覆盖的格子的集合,那么 |S|=2mn。每个这样的 2 \times 2 中至多有两个格子属于 S。
然而所有 4mn 个格子中,恰好有一半的格子属于 S。所以每个 2 \times 2 中恰好 2 个,构成一个 1 \times 2。
从左上角的格子开始依次考虑,可以证明这些就是所有的攻城锤。
根据这个性质,称一个上述的分割中的 2 \times 2 的方格为 上,下,左,右 之一,取决于 1 \times 2 在它中的位置。
性质 2
一个 上 的方格的上方的方格也是 上 的,右边是 上 或者 右,左边是 上 或者 左。其他四种方格类似。
证明显然。
那么,结合以上两条性质,这个图大概是长这样的:
注意到,如果现在就要推式子等方法计算的话,这个生成函数肯定是二元的形式,难以计算,可以用矩阵做到 \Theta(n^6 \log m) 的复杂度,不详细说明。
这一步需要极高的技巧,相当于因式分解了那个难以刻画的二元生成函数。
用两条路径刻画这个图,一条从左上到右下,一条从左下到右上:
那么分成的四块就恰好是 上,下,左,右。
现在这题变成:左上走到右下,每次向右或者向下,有些地方不能走,求方法数。
不能走是因为有 k 个指定的位置,那么这些会限制这条路径。
当然,现在还没有明确说明哪些地方不能走,这里说清楚,下面的例子主要考虑左上到右下的路径。
限制就是,所有 下 的方格和所有 左 的方格和剩下两种方格被这条路径分成两半,也就是,如果把下和左看成 1,其余看成 2,那么这条路径将 1 与 2 分成两个部分。
现在让这个方格表左下为 (0,0),右上为 (m,n)。如果一个 1 类方格的左下角为 (p,q),那么这条路径不能经过任何 x\le p 并且 y \le q 的点,对于 2 类方格类似。下面的图表明了一种可能的能走与不能走的位置。
这里,红色的点表示不能走的点,绿色的线是一条合法的路径,黄色的线把能走到的地方分成了几个矩形。
矩形未必要有长与宽(可以为 0),可能用 s\times t 的点阵( s,t \ge 1)来形容更加合适,下面 点阵 和 矩形 都代表这个意思。
这些矩形是有特殊要求的,不难发现不能走的地方构成了两个简单多边形,这两个多边形的边有水平的和竖直的,用竖直的边分割这个网格图得到了图中所示的矩形,后面的方法会说明为什么要这么分,可以通过上面的图更好的理解这些矩形是怎么刻画出来的。
当然,刻画这些矩形需要将所有放好的块排序并且利用单调栈维护,细节比较多,这里不细说。
考虑最基本的 dp 以及一个没有限制的图,令 dp[i][j] 为到 (i,j) 的合法路径数,那么 dp[i][j]=dp[i][j-1]+dp[i-1][j]。
这个式子可以化成 dp[i][j]=\sum_{k=1}^jdp[i-1][k],也就是一个前缀和的形式。
注意到,如果按照上面的方式将合法区域划分为矩形,那么每个长为 t 的点阵就相当于做 t-1 次前缀和。
我们用到生成函数的知识,如果假设第 i 列(横坐标为 i 的所有点)从上到下的 dp[i][j](0 \le j \le n) 构成生成函数 F_i(x)=\sum dp[i][j]x^j,其中 0 \le i \le m,我们有递推式:
如果不在同一个矩形内,一定在相邻两个矩形内,设这两个矩形的上下高度分别为 $h_1,l_1,h_2,l_2$,如图:
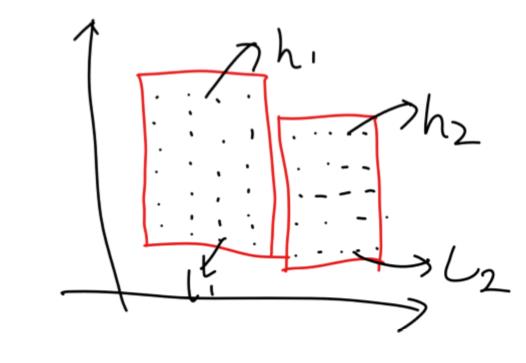
那么,这个生成函数,就是先保留原来 $F_i(x)$ 在 $h_2$ 到 $l_1$ 次项的系数,然后对其做前缀和,为 $G_{i+1}(x)$,然后 $F_{i+1}(x)$ 的系数,不大于 $l_1$ 次项的与 $G_{i+1}(x)$ 相同,$l_1$ 到 $l_2$ 次项用 $G_{i+1}(x)$ 的 $l_1$ 次项系数填充。
这个比较难以用式子进行刻画,所以只能通过文字进行解释。
我们并不需要求出所有的 $F_i(x)$,因为需要的甚至只是 $F_m(x)$ 的一项系数,所以我们求出所有矩形两条宽所在列代表的多项式,相邻多项式之间的转移可以用多项式前缀和以及 $NTT$ 优化就可以在 $n \log n$ 的时间内完成,由于矩形一共 $\Theta(n)$ 个那么这是 $n^2 \log n$ 的,但是这不够优秀,瓶颈在求前缀和上。
如果不用做前缀和,剩下的操作甚至是 $\Theta(n)$ 的。我们考虑一个稍微一般一点的问题:
维护一个多项式,支持三种操作:
(1)做若干次前缀和;(2)查一项系数;(3)加上一个单项式。
(在同一个矩形内的转移规约为(1)操作,相邻矩形转移可以查询 $h_1$ 到 $h_2$ 次项所有系数并依次减掉对应的单项式,然后再做一次前缀和,然后查询 $l_1$ 次项的系数,最后在依次查询 $l_1+1$ 到 $l_2$ 次项的系数,把他们加上与 $l_1$ 次项的系数的差)
此时解法几乎呼之欲出了:
维护一个多项式 $Q(x)$ 与一个整数 $t\ge 0$,我们真实的多项式是 $\dfrac{Q(x)}{(1-x)^t}$,那么对于(1)操作直接修改 $t$,对于 $2$ 操作可以 $O(n)$ 求出卷积的一项,对于 $3$ 操作将这个单项式乘以 $(1-x)^t$ 后加到 $Q(x)$ 上即可,时间复杂度 $O(n^2)$。
作为一道连 `FFT` 都不用的多项式题,快来为良心的出题人点赞吧!
std 供食用,感谢 Kubic,ix35,Karry5307 的付出。
std 进行适当卡常,其实只加上取模优化就能 AC。
```cpp
#include <bits/stdc++.h>
using namespace std;
#define N 9005
#define M 100005
#define LIM 1000000
#define ull unsigned long long
#define ulll __uint128_t
#define mod FM.reduce
#define gc() (P1==P2 && (P2=(P1=buf)+fread(buf,1,LIM,stdin),P1==P2)?EOF:*P1++)
char buf[LIM],*P1,*P2;
int n,c,p,cnt1,cnt2,ans,inv[N],st1[M],st2[M],L[M],R[M];
ull m,d,ds[M],vl[N],z[N];struct Node {int x,v;ull y;}a1[M],a2[M],b1[M],b2[M];
ull rd()
{
ull res=0;char c=0;while(!isdigit(c)) c=gc();
while(isdigit(c)) res=(res<<1)+(res<<3)+(c&15),c=gc();return res;
}
struct FastMod
{
ull b,m;FastMod(ull b=2):b(b),m((ull)(((ulll)(1)<<64)/b)) {}
ull reduce(ull a) {ull q=(ull)(((ulll)(m)*a)>>64),r=a-q*b;return r>=b?r-b:r;}
}FM;
bool cmp1(Node x,Node y) {return x.y==y.y?x.x<y.x:x.y<y.y;}
bool cmp2(Node x,Node y) {return x.y==y.y?x.x>y.x:x.y<y.y;}
int qPt(int x)
{
int C=1;ull res=0;d=mod(d);
for(int i=0;i<=x;++i)
{
if(i) C=mod(mod((d+i-1)*C)*inv[i]);z[x-i]=mod(z[x-i]);
res+=mod(1ull*C*z[x-i]);if(res>=9e18) res=mod(res);
}return mod(res);
}
void upd(int l,int r,int v)
{
int C=1;d=mod(d);for(int i=l;i<=r;++i) vl[i]=0;
for(int i=0;i<=r;++i)
{
if(i) C=mod(mod((d+i-1)*C)*inv[i]);
for(int j=i<l?l:i;j<=r;++j)
{
if(z[j-i]>=p) z[j-i]=mod(z[j-i]);
vl[j]+=mod(1ull*C*z[j-i]);if(vl[j]>=9e18) vl[j]=mod(vl[j]);
}
}C=1;for(int i=l;i<=r;++i) vl[i]=mod(vl[i]),vl[i]=v<vl[i]?v-vl[i]+p:v-vl[i];
for(int i=0,fl=1;i+l<=n && i<=d;++i,fl^=1)
{
if(i) C=mod(mod((d+p+1-i)*C)*inv[i]);
for(int j=l;j<=r && i+j<=n;++j)
{
z[i+j]+=fl?mod(1ull*C*vl[j]):p-mod(1ull*C*vl[j]);
if(z[i+j]>=9e18) z[i+j]=mod(z[i+j]);
}
}
}
void slv(Node a[])
{
cnt1=cnt2=d=st1[0]=st2[0]=ds[0]=0;for(int i=0;i<=n;++i) z[i]=0;
b1[++cnt1]=(Node) {-1,0,0};b2[++cnt2]=(Node) {n+1,0,m};
for(int i=1;i<=c;++i)
if(a[i].v==1 || a[i].v==4) b1[++cnt1]=a[i],++b1[cnt1].y;
else b2[++cnt2]=a[i],++b2[cnt2].x;
sort(b1+1,b1+cnt1+1,cmp1);sort(b2+1,b2+cnt2+1,cmp2);
for(int i=cnt1;i>=1;--i)
{
while(st1[0] && b1[i].x>=b1[st1[st1[0]]].x) --st1[0];
st1[++st1[0]]=i;
}
for(int i=1;i<=cnt2;++i)
{
while(st2[0] && b2[i].x<=b2[st2[st2[0]]].x) --st2[0];
st2[++st2[0]]=i;
}for(int i=1;i<=st1[0];++i) ds[++ds[0]]=b1[st1[i]].y;
for(int i=1;i<=st2[0];++i) if(b2[st2[i]].y<m) ds[++ds[0]]=b2[st2[i]].y+1;
ds[++ds[0]]=0;ds[++ds[0]]=m;
sort(ds+1,ds+ds[0]+1);ds[0]=unique(ds+1,ds+ds[0]+1)-ds-1;
for(int i=1,t1=st1[0],t2=1,t=0;i<=ds[0];++i)
{
while(t1 && b1[st1[t1]].y<=ds[i]) --t1;L[i]=b1[st1[t1+1]].x+1;
while(t2<=st2[0] && b2[st2[t2]].y<ds[i]) ++t2;R[i]=b2[st2[t2]].x-1;
if(!ds[i]) {for(int j=L[i];j<=R[i];++j) z[j]=1;continue;}
d+=ds[i]-ds[i-1]-1;upd(L[i-1],L[i]-1,0);++d;
if(R[i-1]<R[i]) t=qPt(R[i-1]);upd(R[i-1]+1,R[i],t);
}
}
int main()
{
n=rd();m=rd();c=rd();p=rd();FM=FastMod(p);
for(int i=1;i<=n;++i) inv[i]=i==1?1:mod(1ull*inv[p%i]*(p-p/i));
for(int i=1,x1,x2;i<=c;++i)
{
ull y1,y2;x1=rd();y1=rd();x2=rd();y2=rd();
a1[i]=(Node) {x1-1>>1,x1==x2?(x1&1?1:3):(y1&1?2:4),y1-1>>1};
x1=(n<<1)-x1+1;x2=(n<<1)-x2+1;
a2[i]=(Node) {x1-1>>1,x1==x2?(x1&1?1:3):(y1&1?2:4),y1-1>>1};
}slv(a1);ans=qPt(n);slv(a2);printf("%llu\n",mod(1ull*ans*qPt(n)));
puts("I would not copy!");return 0;
}