蒟蒻lhz2022的图论(tarjan算法学习笔记)
lhz2022
·
2025-01-21 22:22:45
·
算法·理论
主要是自学 + 看 bilibili 各位大佬的视频学的,有错误请见谅。
强连通
什么是强联通?
定义一个有向图 G ,如果对于任意两个点 u,v 都存在一条路径(双向都存在), 那么就是个强连通图。
特殊的,单个节点也算强连通图。
强连通分量
是一个图中极大 的强连通子图。(不是最大)
比如说这个有向图。节点 1 ,3 都是强连通分量。
那么节点 0,4,5 构成的那个子图显然也是强连通的,它是不是强连通分量呢?
不是。因为当我们把节点 2 放进来,发现也是强连通的。也就是说,图 G 的子图 G' 是强连通分量的条件是:
不存在一个 $G$ 的子图 $F$ 使得 $F$ 是强连通的且 $G'$ 是 $F$ 的真子图。
## 怎么求强连通分量?
用 Tarjan 算法即可。
至于 dfs 生成树,我觉得没有太大的必要讲。
```cpp
vector<int> g[N];//边
int dfn[N],low[N],stk[N],tp,tot,vis[N];//dfs序,从当前节点开始能够达到的dfs序最小的节点是多少,栈,用来计数dfs序的,是否在栈内
int n,m;
int bel[N];//该节点在哪个强连通分量内
```
```cpp
void tarjan(int x){
low[x]=dfn[x]=++tot;//初始化
stk[++tp]=x;//入栈
vis[x]=1;
for(auto v:d[x]){
if(!dfn[v]){
tarjan(v);
low[x]=min(low[x],low[v]);//显然成立
}
else if(vis[v]){
low[x]=min(low[x],dfn[v]);//这里的v可能指向x的一个之前的节点(这是一条返祖边)
}
}
if(dfn[x]==low[x]){//是强连通分量dfs序最小的一个节点
++scc;
int y=stk[tp];
while(1){//根据dfs的性质,在此之后的这些节点都是在同一个强连通分量里面的。
int u=stk[tp--];
bel[u]=scc;
vis[u]=0;
if(u==x) break;
}
}
}
```
## DAG 上的 dp
先考虑一个比较简单的例子。对 P3387 进行简化。如果本题中的图是一个 DAG,怎么求?
我们设 $dp_i$ 代表到 $i$ 这个节点时可以取得的最大值,则对于每一条边 $[u,v]$ 都有 $dp_v=\max(dp_v,dp_u+val_v)$ 必然成立。
然而,如何以正确的顺序进行 dp 呢?可以对这个图进行拓扑排序,然后按拓扑序求解。
但是本题都带上了【模板】缩点 了,那么就必须将一下缩点。
## 缩点
我们发现在本题中不要求每个节点和边只经过一次,于是我们发现如果存在一个强连通分量,那么就可以得到这个强连通分量中所有点的权值。
这就启发我们把强连通分量抽象为一个节点。就哪之前的图举个例子:
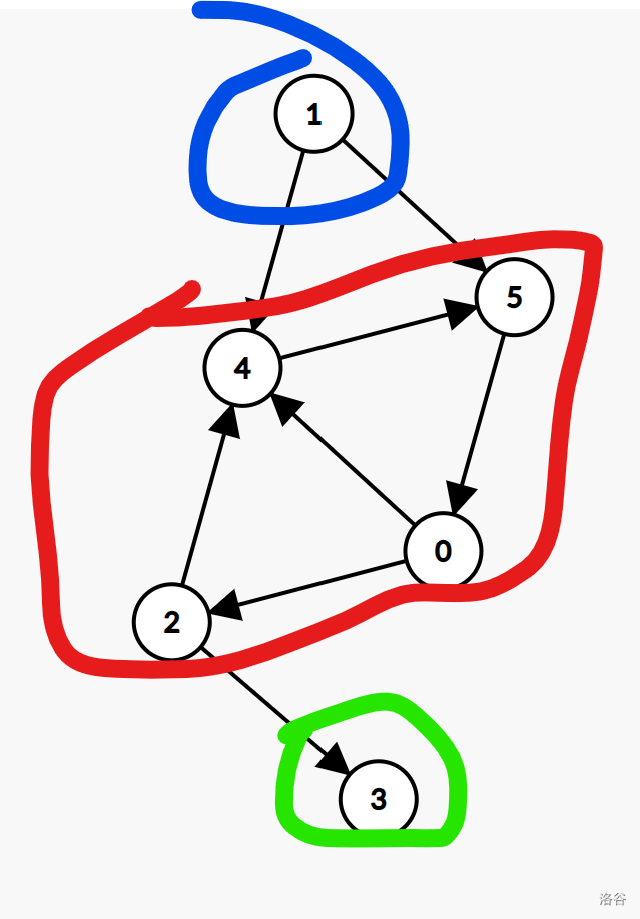
变成这样
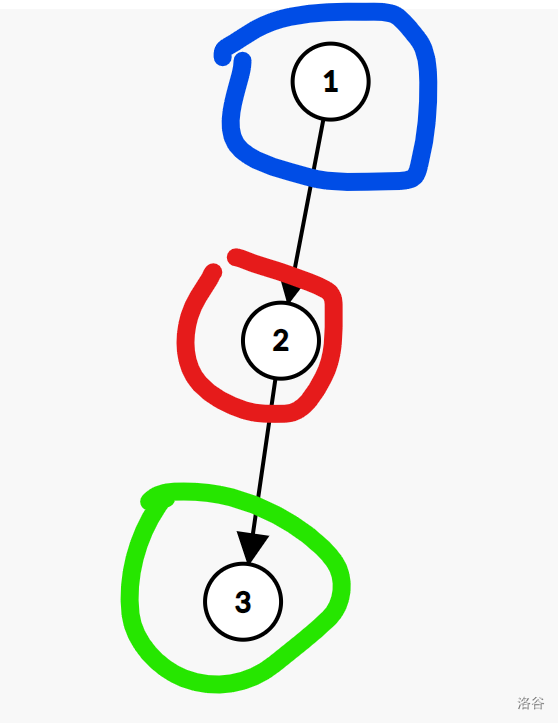
其中每个节点的权值就是之前强连通分量中的所有节点权值之和,这就是缩点。
容易证明,缩点后的图一定是一个 DAG,于是按照上述方法进行 dp 即可。
## 割点
什么是割点?割点是一个无向图中,要是把这个点(和与它连通的边)删除,则原图连通分量增加(或者说,变成了更多小块),如图: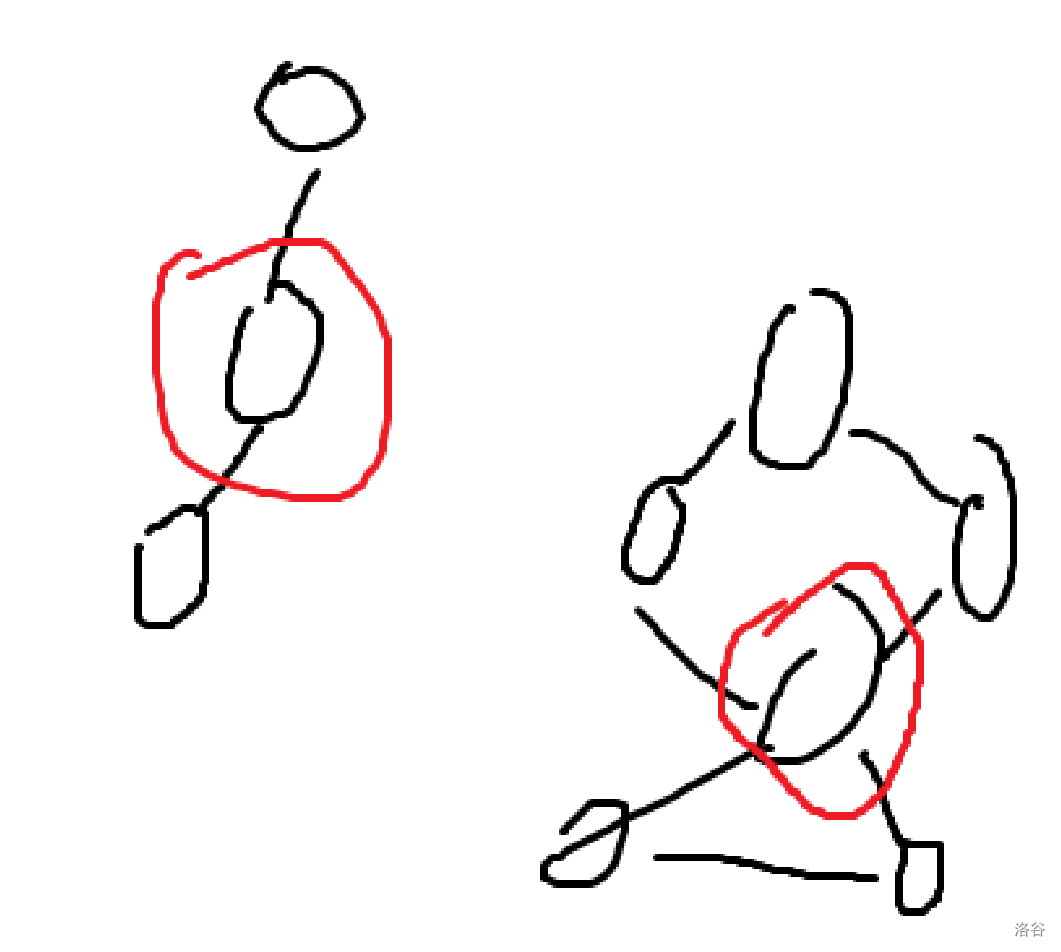圈起来的都是割点。
判断割点的方法是,如果一个节点 $u$ 与其一个子节点 $v$ 满足 $low_v\geq dfn_u$,即可。
上述式子的含义是,如果一个节点不能走到 dfs 序小于其父节点的节点,如图: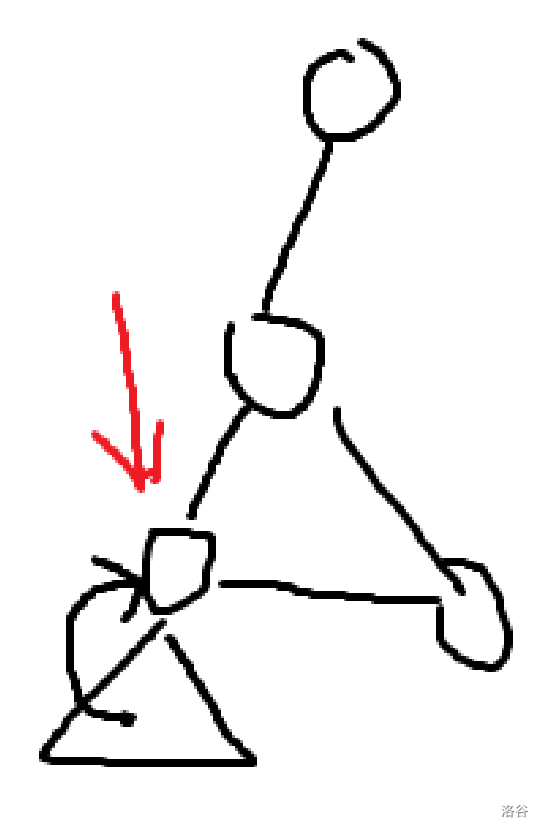我们就可以知道,如果我们删去了这一个点的父节点,那么一定至少这个节点无法与剩余的图联通,所以我们就可以知道这个节点的父节点是割点。
但是再仔细一想,发现,如果这个节点是根节点,发现不能这么算了。
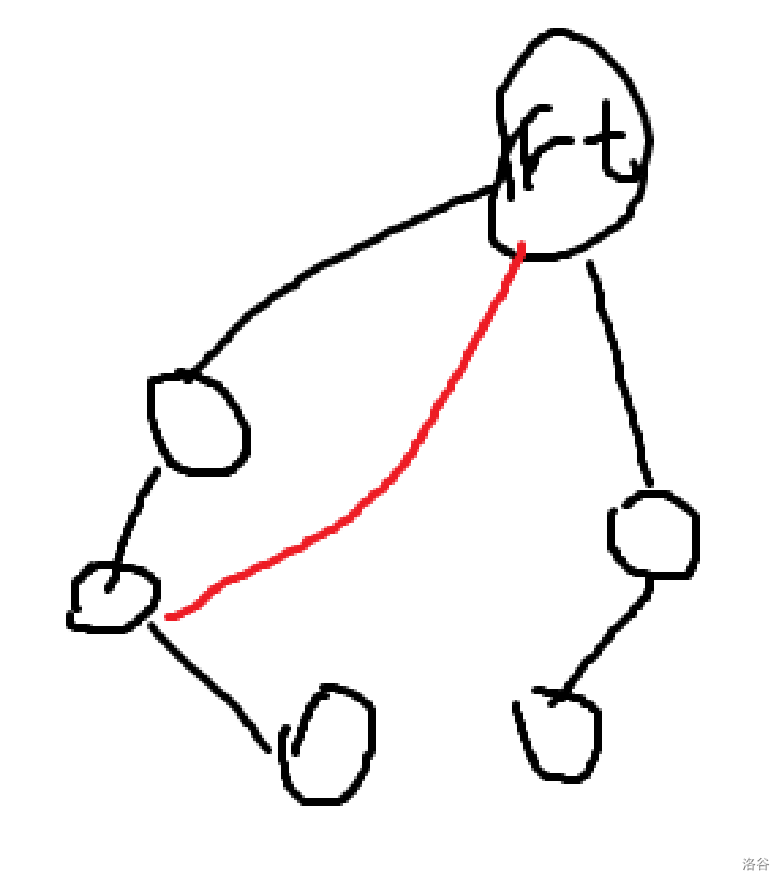
如图,根据 dfs 生成树的性质,我们发现,对于根节点如果是割点,其必有两个或以上个“子树”。所以在写代码的时候需要对根节点特判。
```cpp
void tarjan(int x,bool rt){//rt:是不是根节点
low[x]=dfn[x]=++tot;
vis[x]=1;
int ch=0;
for(auto v:d[x]){
if(!dfn[v]){
tarjan(v,0);
low[x]=min(low[x],low[v]);
if(rt) ch++;//统计
else if(low[v]>=dfn[x]) ans[x]=1;
}
else if(vis[v]){
low[x]=min(low[x],dfn[v]);
}
}
if(rt&&ch>=2) ans[x]=1;
}
```
## 割边
割边的定义是,如果把某一条边删除,则原图不连通,则这条边就是割点。
割边与割点差不多,但是我们需要考虑重边的问题。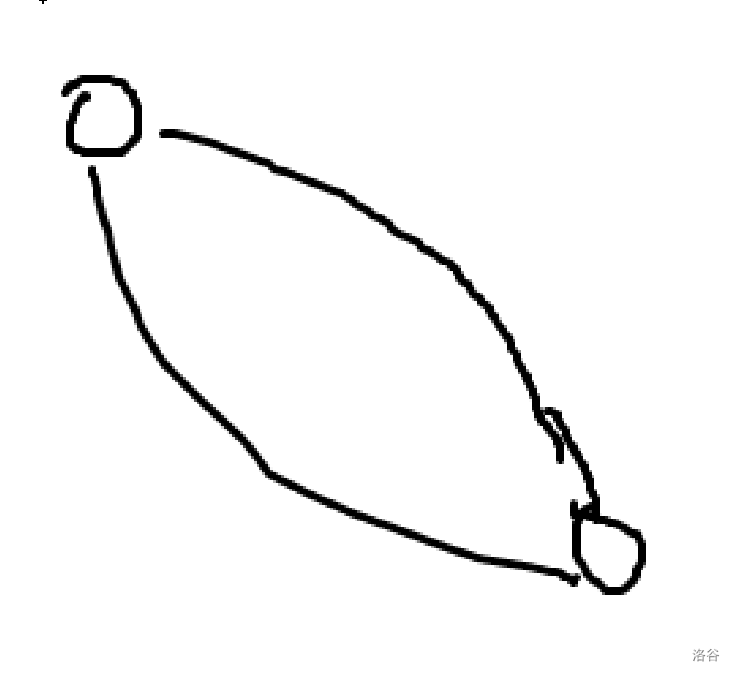
如图,如果有重边,那么这些边不可能是割边。
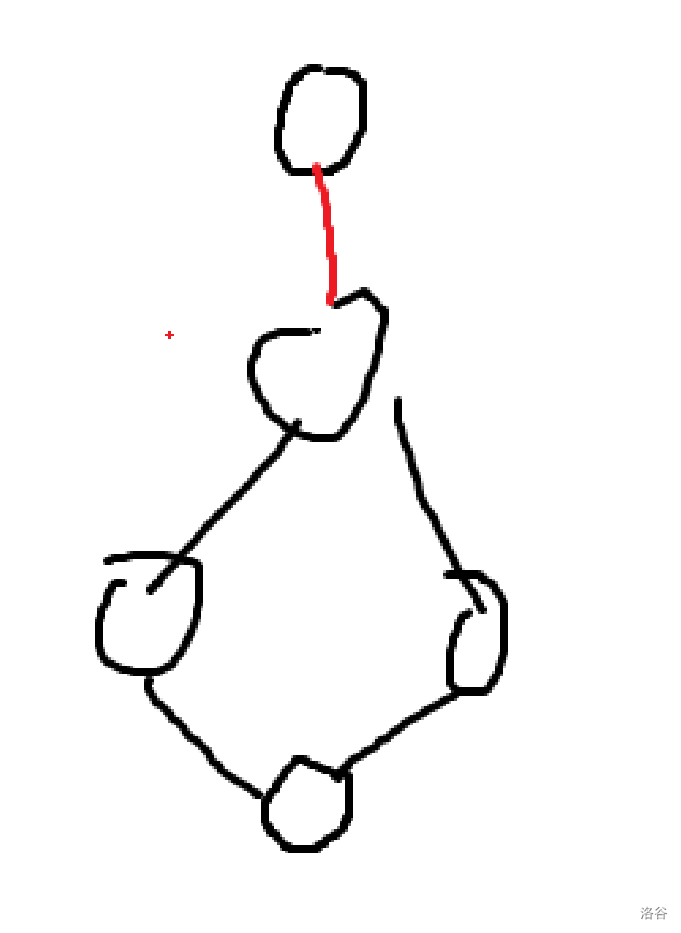
类似于割点的判断,我们发现,如果一个节点 $u$ 与其一个子节点 $v$ 满足 $low_v > dfn_u$,则边 $u,v$ 之间的连边就一定是割边。原因也很简单,因为 $v$ 这个节点显然删去后无法走到 $u$。
割边无需判断根节点,但是要判重。代码有许多细节。
```cpp
//请原谅我冗长复杂的写法
set<pair<int,int>> st;
multiset<pair<int,int>> st1;
void tarjan(int x,int f){
low[x]=dfn[x]=++tot;
vis[x]=1;
int ch=0;
for(auto v:d[x]){
if(!dfn[v]){
tarjan(v,x);
low[x]=min(low[x],low[v]);
if(low[v]>dfn[x]&&st1.count({min(v,x),max(v,x)})<=1) st.insert({min(v,x),max(v,x)});//这条边是割边
}
else if(v!=f&&vis[v]){
low[x]=min(low[x],dfn[v]);
}
}
}
```
几个~~模板题~~练习:
#### 巨简单题 P2002
有 $n$ 个城市,中间有单向道路连接,消息会沿着道路扩散,现在给出 $n$ 个城市及其之间的道路,问至少需要在几个城市发布消息才能让这所有 $n$ 个城市都得到消息。
首先,如果有一个强连通分量,那么在该节点中任意一个节点放出消息则必定使整个分量收到,可以缩点。
缩点完成后直接统计入度为 $0$ 的点的数量即可。
P2835 也是同理,只是改了输入,~~题面变长~~。
#### 简单题 P2341
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢” 是可以传递的 —— 如果 $A$ 喜欢 $B$,$B$ 喜欢 $C$,那么 $A$ 也喜欢 $C$。牛栏里共有 $N$ 头奶牛,给定一些奶牛之间的爱慕关系,请你算出有多少头奶牛可以当明星。
先把喜欢关系建图。
首先如果图是强连通的,那么每个奶牛都可以当明星。
然后就是缩点,然后考虑所有出度为 $0$ 的点。如果只有一个,那么必然这个强连通分量中的奶牛都可当明星。
但是如果不止一个呢?那么就没有牛能当明星。
这些都是比较显然的。
#### 有点思维的 P2476
其实第一问就是上一题了。
主要是第二问:给你一个 DAG,求最少加上几条边即可使其变成强连通分量?
\~\~ 看了一下题解,\~\~ 设入度为 $0$ 的点集是 $P$, 出度为 $0$ 的点集是 $Q
当 |P|\leq|Q| 时
当 |P|=1 则有所有的点都可以从这一个点出发到达,那么只需把 Q 中每一个节点连到这个入度为 0 的点上,答案是 |Q| 。
当 |P|\geq 2 则必然 |Q|\geq|P|\geq2 ,则必有 4 个点 p_1,p_2,q_1,q_2 前两者是 P 中的,后两者是 Q 中的,且从 p_1 可以走到 q_1 ,从 p_2 走到 q_2 。此时,连接 q_1,p_2 。这时的新的 |Q'|=|Q|-1,|P'|=|P|-1 。直到 |P'|=1 变成上面的情况,答案是 |Q| 。
当 |P|\geq |Q| 同理。
所以答案是 \max(|P|,|Q|) 。
稍微有一点改变 P1262
由于外国间谍的大量渗入,国家安全正处于高度的危机之中。如果 A 间谍手中掌握着关于 B 间谍的犯罪证据,则称 A 可以揭发 B。有些间谍收受贿赂,只要给他们一定数量的美元,他们就愿意交出手中掌握的全部情报。所以,如果我们能够收买一些间谍的话,我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍,他手中掌握的情报都将归我们所有,这样就有可能逮捕新的间谍,掌握新的情报。
我们的反间谍机关提供了一份资料,包括所有已知的受贿的间谍,以及他们愿意收受的具体数额。同时我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有 n 个间谍(n 不超过 3000 ),每个间谍分别用 1 到 3000 的整数来标识。
请根据这份资料,判断我们是否有可能控制全部的间谍,如果可以,求出我们所需要支付的最少资金。否则,输出不能被控制的一个间谍。
先吐槽一下题面,根本没有说明什么叫做控制间谍。根据题解的代码,我们才能推断出控制一个间谍的前提是被至少一个 人揭发。这样我们才能对于图进行缩点。
先判断无解的情况,即是否存在既不能被揭发也不能被贿赂的间谍。我们可以通过搜索查明一个间谍是否可以被控制。
然后我们可以证明,如果所有的间谍都可以被控制,我们应当选择缩点之后入度为 0 的所有间谍进行贿赂,这必然是最优的(用反证法可以证明)。
实际上此时这一题就做完了。但是我们发现 Tarjan 算法的实现过程中其实也是搜索。所以我们可以从每个可以贿赂的间谍的位置开始跑 Tarjan,大大的减小了码量。
模板题 P3388
割点模板题。