「HCOI-R1」孤独的 sxz
小胖同学
·
·
题解
「HCOI-R1」孤独的 sxz - 题解
官方题解
Easy Version
【设】
------------
**【分析】**
下图中黄色格子为同学,红色格子为 sxz 。黄色格子里的数为此格子对于 sxz 的曼哈顿距离。
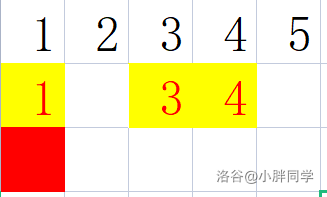
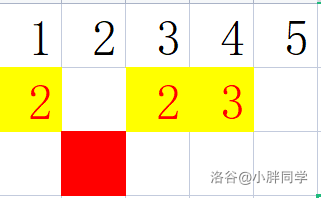
观察可以发现当 sxz 从 $f[i][j]$ 移动到 $f[i][j + 1]$ 时:
矩阵内 $[p,q] (p \in [1 , n] , q \in [1 , i - 1])$ 的曼哈顿距离 $+1$;$[p,q] (p \in [1 , n] , q \in [i , m])$ 的曼哈顿距离 $-1$ 。
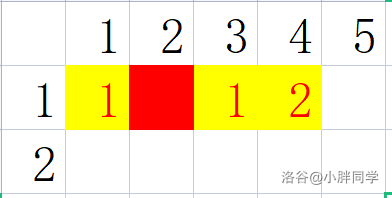
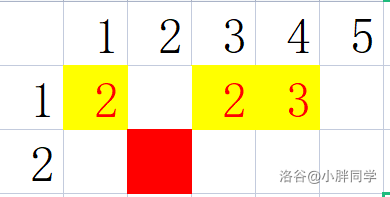
同理当 sxz 从 $f[i][j]$ 移动到 $f[i + 1][j]$ 时:
矩阵内 $[p,q] (p \in [1 , j - 1] , q \in [1 , m])$ 的曼哈顿距离 $+1$ ;
$[p,q] (p \in [j , n] , q \in [1 , m])$ 的曼哈顿距离 $-1$ 。
------------
**【递推式】**
注:$ a[i][j] $ 代表第 $i$ 行第 $j$ 列是否有同学。
$f[i][j] = f[i - 1][j] + cnt_h - cnt_t
cnt_h = \sum _ {p = 1} ^ {n} \sum _ {q = 1} ^ {j - 1} a[i][j]
cnt_t = \sum _ {p = 1} ^ {n} \sum _ {q = j} ^ {m} a[i][j]
f[i][j] = f[i][j - 1] + cnt_l - cnt_r
cnt_l = \sum _ {p = 1} ^ {i - 1} \sum _ {q = 1} ^ {m} a[i][j]
cnt_r = \sum _ {p = i} ^ {n} \sum _ {q = 1} ^ {m} a[i][j]
【实现】
$O(nm)$ 统计 $f[1][1]$ 的值。
$O(nm)$ 拓广。
---
## Hard Version
观察式子可以发现,对于列而言,相邻的两人间的的曼哈顿距离一定是单调的,行同理。
考虑 $O(k)$ 预处理 $f[1][1]$ 的值。
$O(8k)$ 计算 $(1,1)(n,1)(1,m)(n,m)$, $(x_i - 1 , y_i)(x_i + 1 , y_i)(x_i , y_i - 1)(x_i , y_i + 1)$ 和 $(1 , y_i),(n , y_i),(x_i , 1),(x_i , m)
转移乘上距离 f[x_i][y_i] = f[x _ {i - 1}][y _ {i - 1}] + cnt_h \times (x_i - x_{x - 1}) - cnt_t \times (y_i - y_{i - 1}) 就可以了。