[ABC134F] Permutation Oddness【DP】
Tan_Wei_Ye
·
·
题解
说在前面
- 本文部分内容参考了这篇博客和这篇博客。
如有错误请指出。
- 为了方便起见,本篇博客中的 m 为题目给出的 k 。
正题
我们可以把题意转换成球和盒子的配对:
左边的圆形代表球以及球的编号,右边的方形代表盒子,方形右边的数字是盒子的编号。箭头表示将数字放入盒子中。将 P_i 看成数字 i 所在的盒子的编号。
比如上图的 P 为 \{4,3,5,1,2\}。
在每个球之间画一条水平的线,那么这个排列的怪异度就是“球和盒子的连线”与“水平线”的“交点个数”。
可以把往盒子里放数字的过程看作下述 n 阶段决策过程。也就是说,在第 i 个阶段考虑球 i 和编号为 i 的盒子如何处置。
那么我们可以写出以下状态:
答案状态为:$dp[n][0][m]$。
然后给出状态转移方程,我们在下面解释:
$$
\begin{aligned}
dp[i][j][k] &= (2\times j+1)\times dp[i-1][j][k-2\times j] \\
&+ (j+1)\times(j+1)\times dp[i-1][j+1][k-2\times j]\\
&+ dp[i-1][j-1][k-2\times j]
\end{aligned}
$$
我们把一次配对称为在一个球和盒子之间连线。
第一行表示进行了 $1$ 次配对,那么有 $3$ 种情况
1. 第 $i$ 个球与没配对的 $j$ 个盒子配对 ,共有 $j$ 种。
2. 第 $i$ 个盒子与没配对的 $j$ 个球配对 ,共有 $j$ 种。
3. 第 $i$ 个球与第 $i$ 个盒子配对 ,共有 $1$ 种。
根据加法原理,共有 $2 \times j + 1$ 种方法。
第二行表示进行了 $2$ 次配对,那么有 $2$ 种情况
1. 第 $i$ 个球与没配对的 $j+1$ 个盒子配对 ,共有 $j+1$ 种。
2. 第 $i$ 个盒子与没配对的 $j+1$ 个球配对 ,共有 $j+1$ 种。
根据乘法原理,共有 $(j +1) \times (j + 1)$ 种方法。
第三行表示进行了 $0$ 次配对,那么有 $1$ 种情况, $1$ 种方法。
现在唯一的问题,也是当时我自己做的时候困扰我好久的问题:为什么 $k$ 要从 $k-2\times j$ 转移过来。
我们可以这样想:
因为最终的答案肯定是所有球和盒子都配对完了的,所以状态中的 $j$ 可以有另一种解释: $1 \sim i$ 这些球中有 $j$ 个要放到编号大于 $i$ 的盒子里。
每次转移时,因为我们把第 $i$ 个盒子进行了配对,所以未配对的球连的线会下移一行,会导致多出 $2 \times j$ 个交点,举个例子:
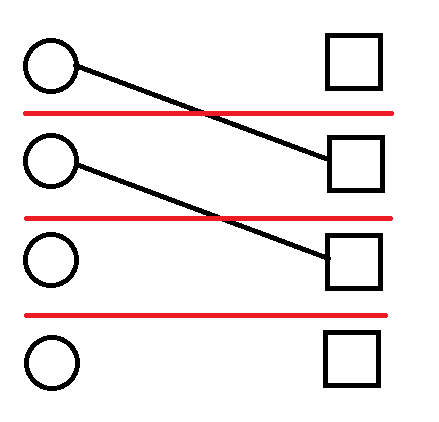
------------
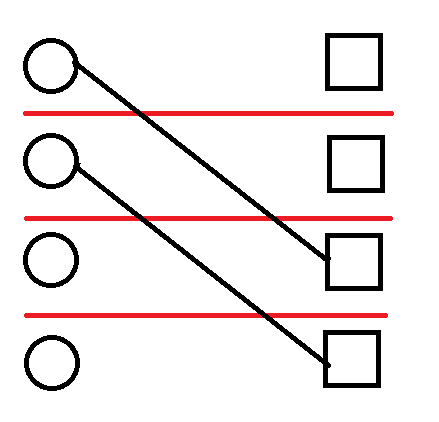
(交点从 $2$ 个变成了 $4$ 个,多了 $2$ 个,但还要算反着的,所以多了 $4$ 个)
其他应该没什么问题了。
## 代码
```cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=55;
const int mod=1e9+7;
int n,m;
int dp[N][N][N*N];
signed main()
{
cin>>n>>m;
if(m&1) return puts("0"),0;
dp[0][0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=i;j++)
for(int k=2*j;k<=m;k+=2)
{
dp[i][j][k]=((2*j+1)*dp[i-1][j][k-2*j]%mod
+(j+1)*(j+1)*dp[i-1][j+1][k-2*j]%mod)%mod;
if(j>=1) dp[i][j][k]=(dp[i][j][k]+dp[i-1][j-1][k-2*j])%mod;
}
cout<<dp[n][0][m];
}
```
------------
## 时间复杂度: $O(n^4)