题解 P1665 【正方形计数】
Huami360
·
·
题解
不知道为什么O(n^4)的玄学方法能过,正解显然是O(n^2)的,枚举对角线,然后算出另外两点判断存不存在。
关键就在怎么通过对角线算出另外两点的坐标。
先贴公式。
int midx = (x[i] + x[j]) / 2;
int midy = (y[i] + y[j]) / 2;
int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);
$(x1,y1),(x2,y2)$是我们算出来的另两个点的坐标。
怎么来的呢?
如图,
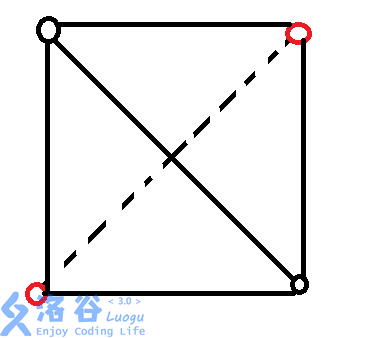
黑点是我们枚举的对角线,红点就是我们要算的另外两点。
我们算出对角线的重点$(midx,midy)$。
然后做几条辅助线,如图:
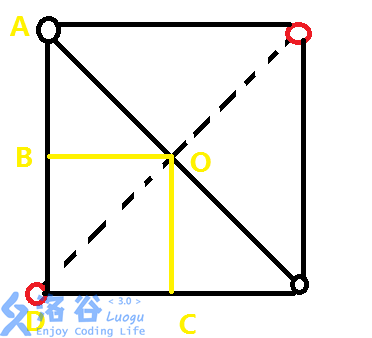
图中的$OC$,$OB$是垂直于$x$轴和$y$轴,并不一定垂直于正方形的边。
易得△$ABO$ ≌ △$DCO$,于是,这两个三角形以$AB$,$CD$为底的高也相等,现在是不是就能理解这个公式了。
贴代码$O(n^2)$常数小
```cpp
#include <cstdio>
#define Open(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout);
#define Close fclose(stdin);fclose(stdout);
int n, ans;
int x[60000], y[60000], vis[1100][1100], xs[1100][1100];
int main(){
Open("count");
scanf("%d", &n);
for(int i = 1; i <= n; ++i){
scanf("%d%d", &x[i], &y[i]);
x[i] = (x[i] + 51) << 1; //防止负数和小数
y[i] = (y[i] + 51) << 1;
vis[x[i]][y[i]] = 1;
}
for(int i = 1; i < n; ++i)
for(int j = i + 1; j <= n; ++j){
int midx = (x[i] + x[j]) / 2;
int midy = (y[i] + y[j]) / 2;
int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);
if(x1 <= 0) continue; if(x2 <= 0) continue;
if(y1 <= 0) continue; if(y2 <= 0) continue;
if(vis[x1][y1] && vis[x2][y2]) ++ans;
}
printf("%d\n", ans >> 1);
return 0;
}
```