题解:CF1874C Jellyfish and EVA
Ray_Wu
·
·
题解
Luogu | Codeforces
题目大意
有一张 n 个点 m 条边的有向图,任意一条边 u\rightarrow v 满足 u<v。
你在点 1,可以进行若干次移动。对于每次从点 u 开始的移动,你需要遵循以下规则:
首先,选择一个 u 的出点 v。
然后,从所有 u 未被销毁的出点中等概率随机选择一个出点 w。若 v=w,则移动到 v;否则销毁 (u,v),(u,w) 两条边,之后不能再走也不会在任何情况下被考虑到。
从点 1 开始走,在每个点 u 选择最优的点 v,使得成功走到点 n 的概率最大。输出此概率。
### 思路
首先设 DP 状态。
我们不妨设 $f_i$ 表示在全局最优解下从节点 $i$ 走到 $n$ 的概率。
对于每个节点 $u$,它的每个后继节点 $v$ 都有 $f_v$ 属性,按照题目要求:
- 当 $u \to v$ 这条边仍然保留时:我们肯定会优先选择 $f_v$ 最大的 $v$。
- 否则如果 $u \to v$ 已被删除:将会在剩下的 $v$ 中选择最优的点($f_v$ 最大)。
- 重复以上过程,直到前往下一个节点或者停止操作。
我们可以先写一个转移方程:
$$
f_u = \sum_{(u \to v) \in E} f_v \times p_{u \to v}
$$
其中 $p_{u \to v}$ 表示 $u$ 前往 $v$ 的概率。
为了表示 $p$,我们定义 $g_{i, j}$ 表示对于一个出度为 $i$ 的节点 $u$,前往第 $j$ 优的后继节点的概率。
那么上面的式子可以写成:
$$
f_u = \sum_{(u \to v_i) \in E} f_{v_i} \times g_{d_u, i}
$$
其中 $v$ 为 $u$ 的后继节点,$f_{v_1} \ge f_{v_2} \ge \cdots \ge f_{v_{d_u}}$,$d_u$ 表示 $u$ 的后继节点个数。
那么为了推出答案 $f_1$,我们需要求出 $g$。
可以发现,$g$ 的取值和具体是哪个 $u$ 无关,只和出度以及优先度有关。因此它可以预处理出来。
考虑如何预处理 $g$。
对于优先度最高的后继节点,成功前往它的概率是 $\frac{1}{d}$。所以 $g_{i, 1} = \frac{1}{d}$。
那么对于 $g_{i, j}(j > 1)$,我们如何转移?
分类讨论,删除边存在两种情况:
- **情况一:**
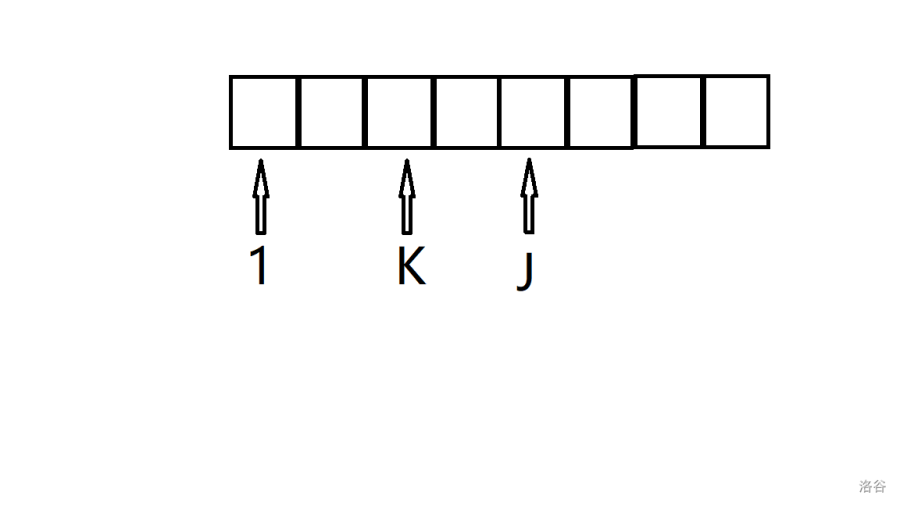
$k < j$,$u$ 的后继结点 $k$ 优于 $j$,此时我们可以从 $g_{i - 2, j - 2}$ 转移到 $g_{i, j}$(删去 $1$ 和 $k$ 后,$j$ 从原来的第 $j$ 优变为了 $j - 2$ 优)。
那么走这条边的概率是多少呢?
由于 $1 < k < j$,那么 $k$ 一共有 $j - 2$ 种选择,一共 $i$ 条出边,所以 $p_{u \to j} = \frac{j - 2}{i}$。
该情况对 $g_{i, j}$ 的贡献为:
$$
g_{i - 2, j - 2} \times \frac{j - 2}{i}
$$
- **情况二:**
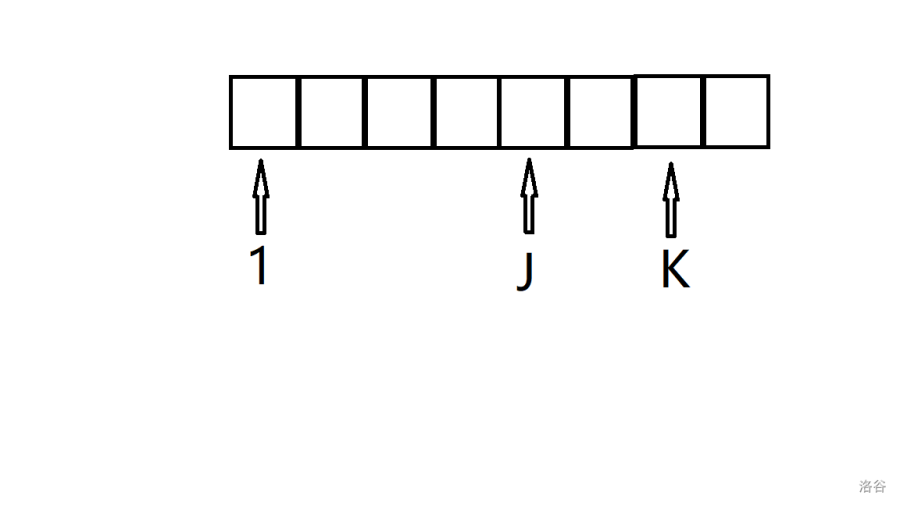
$k > j$,$k$ 的优先度低于 $j$。那么选择该边的概率为 $\frac{i - j}{i}$($j$ 后面的点都可以选)。
原来的第 $j$ 优变为了第 $j - 1$ 优,故从 $g_{i - 2, j - 1}$ 转移过来。
所以该情况对 $g_{i, j}$ 的贡献为:
$$
g_{i - 2, j - 1} \times \frac{i - j}{i}
$$
综上:
$$
g_{i, j} = g_{i - 2, j - 2} \times \frac{j - 2}{i} + g_{i - 2, j - 1} \times \frac{i - j}{i}
$$
所以做完了。
**做法综述:**
1. 预处理 $g$。
2. 读入,根据给出的图算出 $f$。
3. 答案为 $f_1$。
时空复杂度 $O(n^2 + m \log m)$。
[AC CODE](https://codeforces.com/contest/1874/submission/277264411)
---
### 注意事项
- 多组数据,记得清空;
- 计算 $f$ 应当从 $n$ 到 $1$(每条边 $u \to v$ 满足 $u < v$)。
- 记得用 double,注意输出 double 的精度。
---
### 其他
希望这篇题解能给您带来帮助。
感谢 @[wjwWeiwei](https://www.luogu.com.cn/user/547295) 对本篇题解的巨大贡献。