题解 P2501 【HAOI2006】数字序列
lsoer
·
·
题解
有一个长度为 n 的整数序列 a ,现在希望通过改变其中的一些数字的大小来使这个序列变成一个单调上升的序列(右边的数字大于左边的数字,不能等于)。
问题一:
最少需要改变几个数字才能达成目标。
问题二:
在改变数字数最少的情况下,对所有被改变数字改变量的和最小为多少。
一,解决问题一
第1步:转化为序列 b
改变的数字最少,就是不被改变的数字最多。我们从哪些数字可以不被改变来开始思考。
首先,题目对我们选择改变哪个数字没有限制。所以单独考虑某一个数字能否不改变似乎没什么意义,“我们想保住它,就能保住它”。
那么考虑两个数字,如果我们想让某两个数字不被改变,它们就可以不被改变吗?
显然这是不行的,比如序列 3,1 ,有 a_1>a_2 ,它们不满足右边的数字大于左边的数字,是一定要改变其中的一个才能达成目标的。
那么对于 a_i 和 a_j ( i<j ,即 a_i 在 a_j 左边),如果 a_i<a_j ,它们就一定可以都不被改变吗?
其实还是不行,考虑序列 1,1,2 ,虽然有 a_1<a_3 ,但 a_1 和 a_3 中还是必须有一个被改变。原因在于二者之间的 a_2 必须满足 a_1<a_2<a_3 ,但 a_1 和 a_3 数值上太过接近,结果 a_2 “无处可去”了。
由此我们可以明白 a_i 和 a_j 间需要有一些空间来“放下”它们之间的数,不然就必须有一个被修改。
即需要满足 $a_j-a_i-1 \geqslant j-i-1$ ,即 $a_j-a_i \geqslant j-i$ ,也就是 $a_i-i \leqslant a_j-j$ 。
记 $b_i=a_i-i$ ,那么对于 $a_i$ , $a_j$ 如果满足 $b_i \leqslant b_j$ 那么它们两个都可以不被改变。
#### 第2步:转化为最长不下降子序列
我们可以发现一件有意思的事情:如果 $b_i \leqslant b_j$ ,且 $b_j \leqslant b_k$ ( $j<k$ ),那么有 $b_i \leqslant b_k$ ,这表明如果 $a_i$ 和 $a_j$ 可以同时不被改变,且 $a_j$ 和 $a_k$ 可以同时不被改变,那么三者就是可以同时不被改变的。这个结论还可以向更多的数字拓展。
**这使得我们的问题可以转化为:在新构造的 $b$ 序列中寻找最长的一个子序列,它满足对于其中的任意两个数字都有左边的不大于右边的。**
显然这个序列所对应的 $a$ 序列的子序列中每个数字是可以同时不被改变的(原因见上上一段),而它又是最长的,这就满足了我们的要求:尽量多保留数字不被改变。
最长不下降子序列的 $n\log(n)$ 做法可见 [P1020 导弹拦截](https://www.luogu.com.cn/problem/P1020) ,这里只简单提一下。
1. 建立一个队列,并从左到右遍历原数组。
1. 对于当前遍历的数,如果它不小于队列的最后一个数字,就将它接在队列的最后。
1. 不然就从左到右寻找队列中第一个大于它的数字(这里用二分查找)并替换之。
1. 每个数字进入队列的位置就代表了以它为尾的最长不下降子序列的长度。
我们找到的 $b$ 序列的最长不下降子序列的长度就是我们最多能不改变的数字数,用 $n$ 减就可以得到最少需要改变的数字数。
### 二,解决问题二
通过上边的分析,我们可以得知哪些数字需要改变,哪些需要保留。现在我们需要考虑一个方案使改变量尽量小。
我们可以发现:一旦我们改变 $a_i$ ,$b_i$ 也会跟着改变。由于 $b_i=a_i-i$ ,$i$ 不变, $a_i$ 和 $b_i$ 的改变量应该是相同的。
我们希望改变 $a_i$ ,使 $a$ 序列变成单调上升的序列,并且想尽量少改。
我们可以改变 $b_i$ ,使 $b$ 序列变成单调不降的序列,并且想尽量少改。
可知二者的答案是相同的,现在我们就把上面的问题转化为了下面的问题。
现在考虑我们找到的最长不下降子序列,这个序列中的两个相邻数之间可能会有一些其它不在序列中的数:
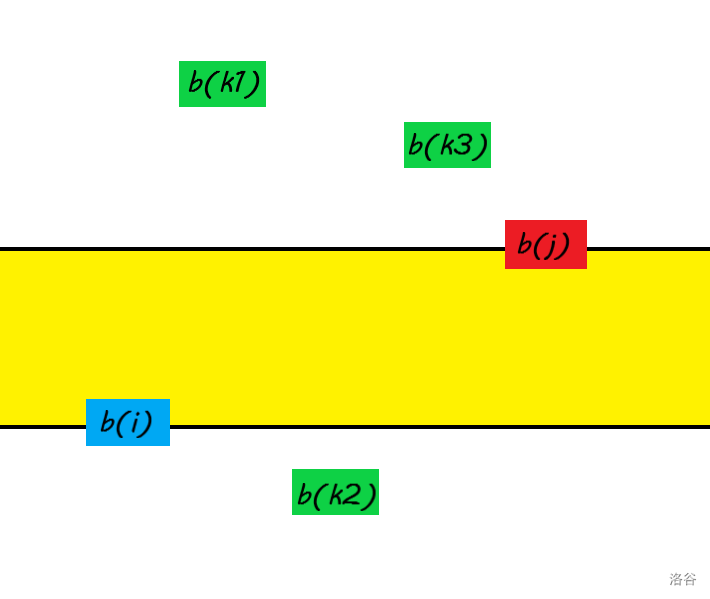
$b_i$ 和 $b_j$ 是序列中的数,它们之间有 $b_{k1}$ , $b_{k_2}$ , $b_{k_3}$ 这三个数。
注意这三个数都不在图中的黄色区域里面或边上,不然它们就应该是最长不下降子序列的一部分,即有:$b_i$ 和 $b_j$ 间任何一个数 $b_k$ 都满足 $b_k>b_j$ 或 $b_k<b_i$ 。
我们现在希望改变 $b_{k1}$ , $b_{k2}$ , $b_{k3}$ 的大小使它们都在黄色区域的里面或边上,且满足左边的数不大于右边的数。
结果大概是这样的:
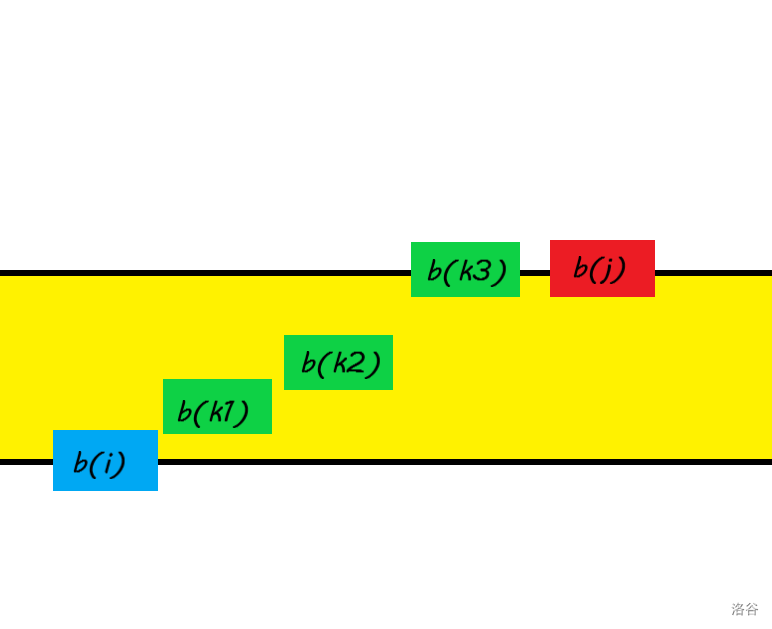
但我们希望尽可能少的改变每个数,这就需要去找到那个最优的方案。
但无论如何,每一个方案,不管是否最优,都需要这一步:将中间的这些数移动到黄色区域的边界上,即:
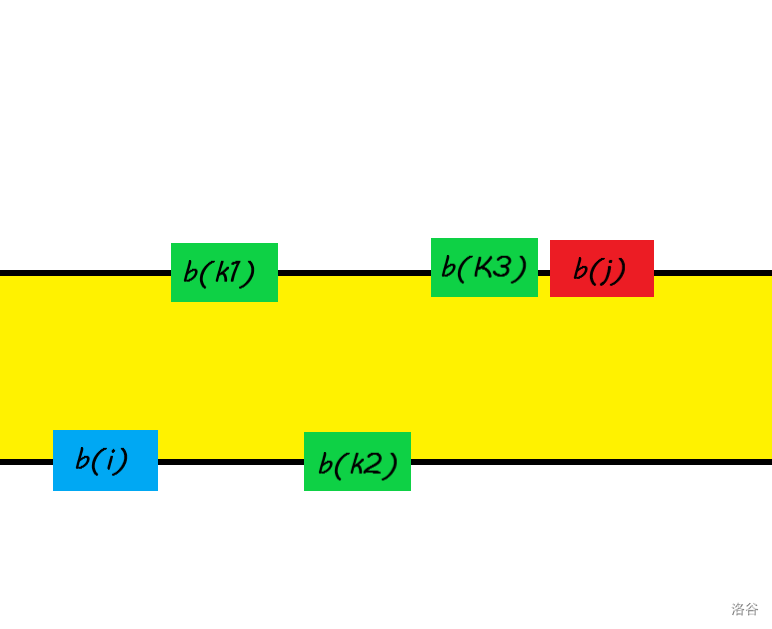
这是因为不管怎样,最后它们这些数最后都要处于黄色区域里面或边上,先移到边上总管是没错且必须的。
如何寻找最优解呢?
可以证明:**最优解之一一定是所有中间的数都在黄色区域的边界上的情况**。
这是一个例子:
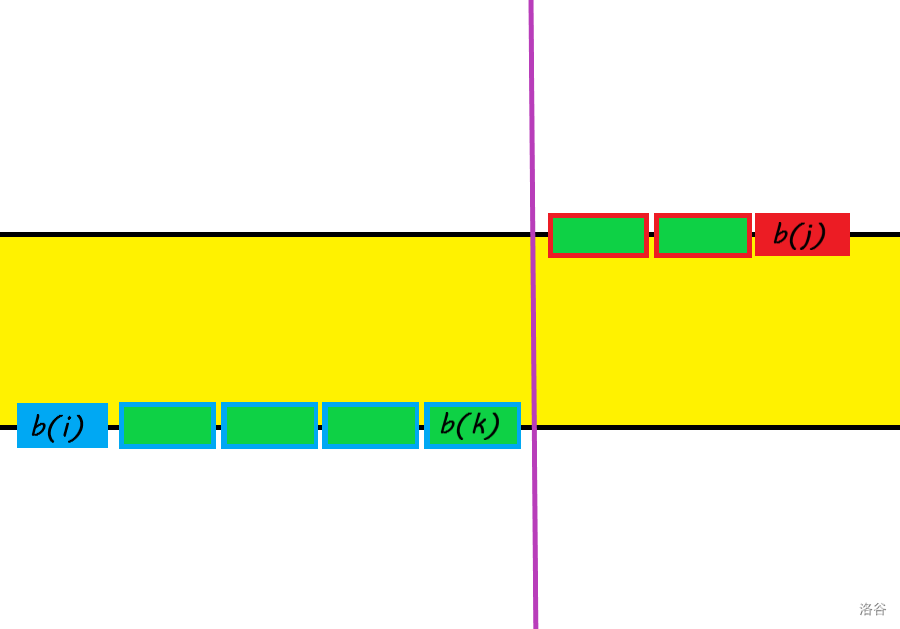
换句话说就是:找到满足 $i \leqslant k<j$ 的 $k$ 并使 $b_{i+1},b_{i+2},...,b_k=b_i$ 且 $b_{k+1},...,b_{j-2},b_{j-1}=b_j$ ,一定存在一个 $k$ 使得这种修改方案是一个最优解。
就将这种修改方案称为“**了不起的优质修改方案**”吧!
为什么它是最优解(之一)呢?
假设最优解不是这样的,而是:
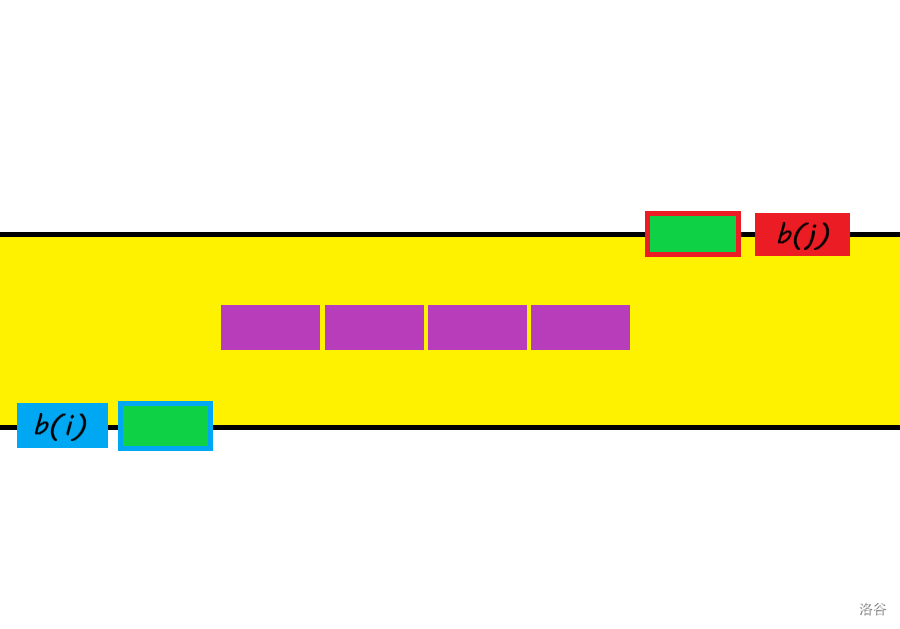
分析一下中间连在一起紫色的那一堆数(“紫色平板”),将它们分为两类: $b_X$ 和 $b_Y$ ,在被改变之前,有 $b_X<b_i$ , $b_Y>b_j$ 。也就是说 $b_X$ 是从黄色区域下方“升”上来的, $b_Y$ 是从黄色区域上方“降”下来的。
为了最小的改变量,我们希望 $b_X$ 尽量少“升”, $b_Y$尽量少“降”。
考虑紫色的那堆数里 $b_X$ 的数量为 $N_X$ , $b_Y$ 的数量为 $N_Y$ 。
- **情况一:$N_X>N_Y$**
这时如果我们让这个“紫色平板”下降,由于 $b_X$ 的数量更多,总改变量的减少比增加多(**$b_X$ 下降会使总改变量减少, $b_Y$ 上升会使总改变量增加**),总改变量会减少,这意味着上面的情况不是最优解,将“紫色平板”降到不能再降的“了不起的优质修改方案”才是更优的解。
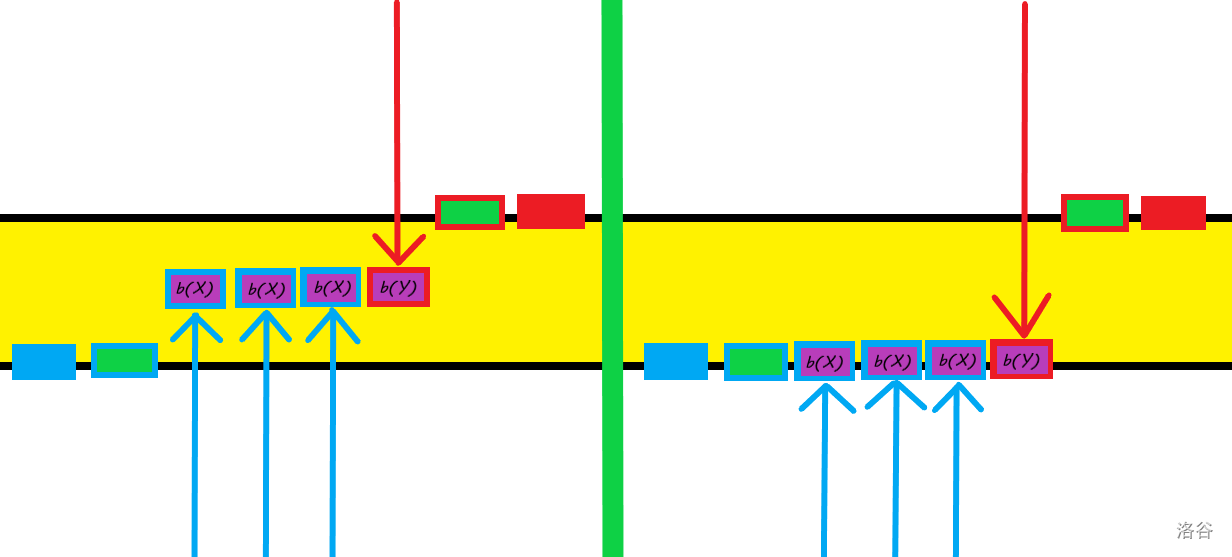
- **情况二:$N_X<N_Y$**
和上面相似,这时我们让“紫色平板”上升,由于 $b_Y$ 更多,总改变量的减少还是会比增加多,“了不起的优质修改方案”再一次替代了此方案,成为了更优的解。
- **情况三:$N_X=N_Y$**
这时,由于 $b_X$ 的数量和 $b_Y$ 一样多,“紫色平板”无论上升还是下降都不会使总改变量改变(增加的和减少的一样多),“了不起的优质修改方案”和此方案一起都是最优解。
很好,有一个“紫色平板”的情况下,“了不起的优质修改方案”是最优解。但如果有多个“紫色平板”呢?
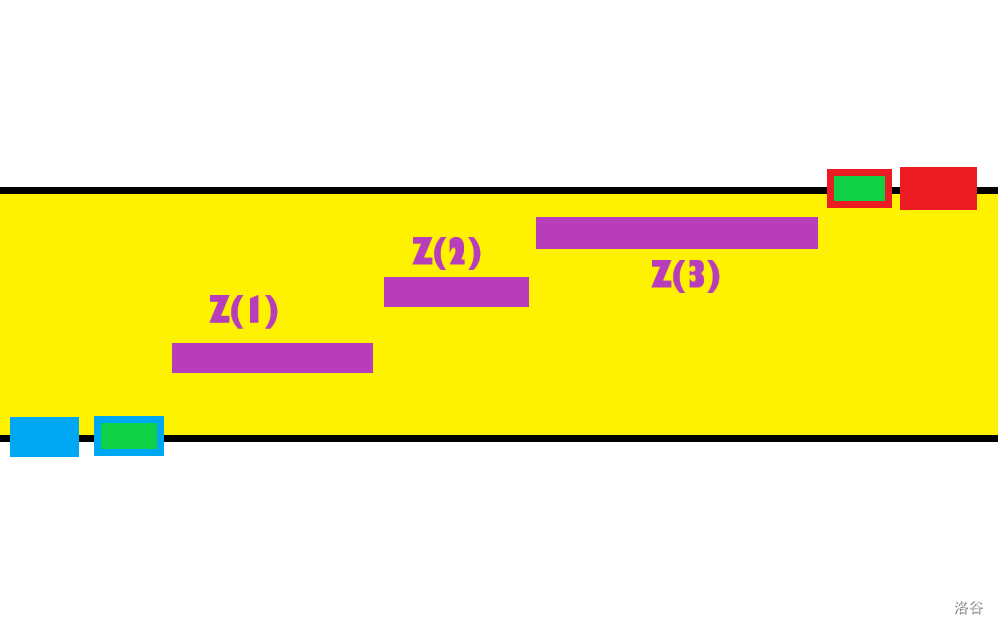
处理方法如下:
1. 从左到右遍历这些“平板”,对于一个“平板”考虑它的 $N_X$ 和 $N_Y$ 的大小比较。
1. 若 $N_X>N_Y$ 将它下降至边界。
1. 若 $N_X<N_Y$ 将它上升使它与右边的那一块“平板”“合为一体”,之后一起处理(如果右边没有“平板”就上升至边界”)
1. 若 $N_X=N_Y$ 就······随便,反正不影响结果。
这样最后还是成为了“了不起的优质修改方案”,证明了“了不起的优质修改方案”是更优的。
如此,可以证明我们的方案是对的,**只要枚举 $k$ 的所有值就能找到最优解**。
### 三,代码实现细节
懂得了方法不一定代表你能通过这道题,本题的代码要求还是有不少的:
#### 1,多个最长不下降子序列
事实上 $b$ 序列的最长不下降子序列可能有多个,为了第二问能找到最优解我们需要将它们全部记下来。
实现方法是考虑 $b$ 序列中每个数最长的以其结尾的不下降子序列长度,并用一个vector数组将同一长度的数记下来。查询时反向寻找即可。
这样做的好处是可以方便之后的动态规划状态转移。
#### 2,dp
考虑 $b$ 序列中的数 $b_i$ ,最长的以它为结尾的不下降子序列的长度为 $l_i$ ,以它为最后一个数的子任务(找到的最长不下降子序列以它为结尾)最优解为 $dp_i$ 。有:
$$dp_j=min(dp_i+min(\sum_{q=i+1}^k|b_q-b_i|+\sum_{q=k+1}^{j-1}|b_q-b_j|))$$
$$l_i+1=l_j,b_i \leqslant b_j ,i \leqslant k < j$$
上述的两个求和使用前缀和优化加速。
#### 3,最左和最右
我们的最长不下降子序列左边和右边可能会有数,为了不落下它们,设定一个虚拟的 $b_0$ 和 $b_{n+1}$ ,具体请看代码。
小声说一句,记得开long long
### 四,代码
```
#include<iostream>
#include<vector>
#include<algorithm>
#define inf 10000000000
using namespace std;
inline long long min(long long x,long long y){return x<y?x:y;}
inline int abs(int x){return x>0?x:-x;}
int a[35010],b[35010];
long long sum1[35010],sum2[35010];
int le[35010];//每个数最长的以其结尾的不下降子序列长度
long long dp[35010];
int lin[35010],ln;//算最长不下降子序列所用序列
vector<int> v[35010];
int main()
{
int n;
cin>>n;
for (int i=1;i<=n;++i)
{
cin>>a[i];
b[i]=a[i]-i;
dp[i]=inf;
}
int pl;
for (int i=1;i<=n;++i)
{
if (!ln||lin[ln-1]<=b[i])
{
lin[ln++]=b[i];
v[ln].push_back(i);
le[i]=ln;
}
else
{
pl=upper_bound(lin,lin+ln,b[i])-lin;
lin[pl]=b[i];
v[pl+1].push_back(i);
le[i]=pl+1;
}
}
cout<<n-ln<<endl;
//第一问结束
v[0].push_back(0);
b[0]=-200000;//虚拟b(0)
le[n+1]=ln+1;
b[n+1]=200000;
dp[n+1]=inf;//虚拟b(n+1)
for (int j=1;j<=n+1;++j)//枚举j
for (int p=0;p<v[le[j]-1].size();++p)
{
int i=v[le[j]-1][p];//枚举i
if (i>j||b[i]>b[j])
continue;
sum1[i]=sum2[j]=0;
for (int q=i+1;q<j;++q)
sum1[q]=sum1[q-1]+abs(b[q]-b[i]);
for (int q=j-1;q>i;--q)
sum2[q]=sum2[q+1]+abs(b[q]-b[j]);
//两个前缀和
long long ans=inf;
for (int k=i;k<j;++k)
ans=min(ans,sum1[k]+sum2[k+1]);
dp[j]=min(dp[j],dp[i]+ans);
}
cout<<dp[n+1];
//第二问结束
return 0;
}
```