题解:CF1906H Twin Friends
Greenzhe
·
·
题解
:::info[提示 1]{open}
:::
:::success[解答]{open}
记 $b_i$ 为 $A$ 中字符 $i$ 出现的次数,大写字母依次编号为 $1 \sim 26$。
如果我们已经确定了每个 $A_i$ 对应 $B$ 中的位置,
那么最后答案就为(不考虑 $A$ 顺序的方案数)$\times \dfrac{n!}{b_1!b_2!\cdots b_{26}!}$,后者即为 $A$ 的不同排列总数。
:::
:::info[提示 2]{open}
现在问题就转化为:对于每个位置上的字符 $A_i$,都要在 $B$ 中匹配一个字符 $i$ 或 $i+1$。
记 $c_i$ 为 $B$ 中字符 $i$ 出现的次数。
你能刻画出这个模型并设计 DP 方程吗?
:::
## Solution
注意到相同字符之间是不区分的,答案只和 $b_i, c_i$ 有关。
这相当于把每个 $b_i$ 划分成两部分,一部分对应 $c_i$,一部分对应 $c_{i+1}$。所有 $b_i$ 必须分完,而 $c_i$ 则不必。
令 $f_{i,j}$ 表示**已经分完 $b_1 \sim b_i$,其中 $b_i$ 给 $c_{i+1}$ 分了 $j$ 的方案数。**
显然有 $f_{0,0}=1$,所求即为 $f_{26,0}$。
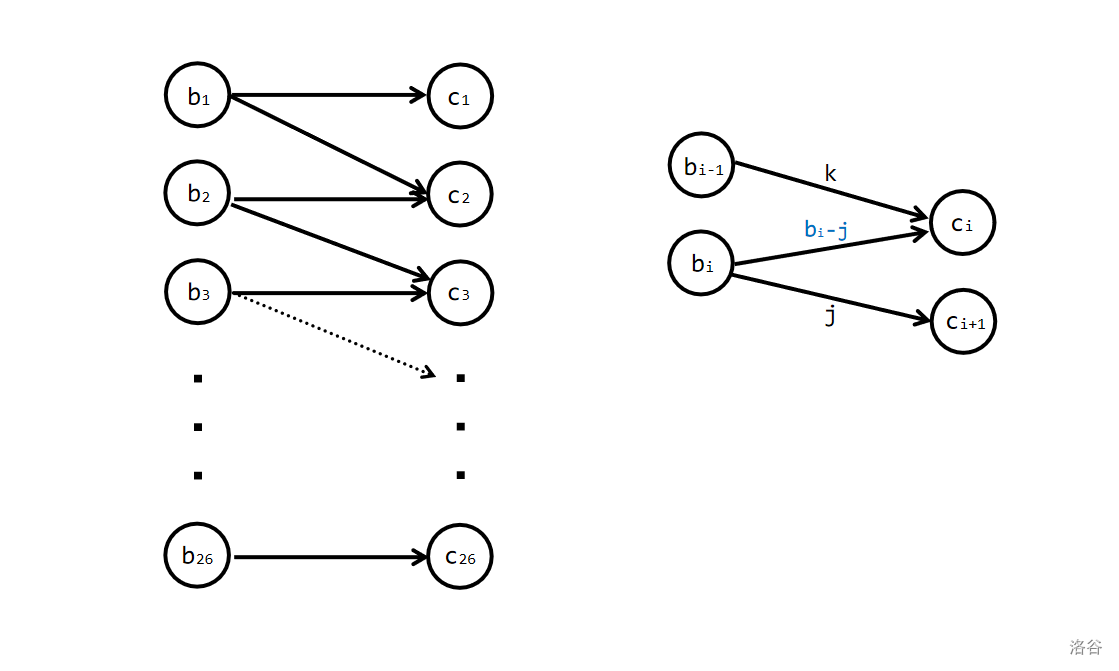
不难画出如上示意图。
注意到 $k+b_i-j \le c_i$,由此得到转移方程:
$$f_{i,j}=\sum_{k=0}^{c_i-b_i+j} f_{i-1,k} \times \binom{b_i}{j}$$
显然这个 $\sum_{k}$ 可以用前缀和优化掉。预处理阶乘组合数,复杂度 $\mathcal O(n \times |\Sigma|)$,其中 $|\Sigma|$ 为字符集大小 $26$。
答案为 $f_{26,0} \times \dfrac{n!}{b_1!b_2!\cdots b_{26}!}$。
```cpp
// Problem: CF1906H Twin Friends
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1906H
// Memory Limit: 1000 MB
// Time Limit: 1000 ms
// Author: Greenzhe_qwq
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD=998244353;
const int N=4e5+5;
int n,m,c[30],b[30];
char s1[N],s2[N];
ll fac[N],ifac[N],dp[30][N],sum[N];
inline ll qpow(ll a,ll b){
ll res=1;
while(b){
if(b&1) res=res*a%MOD;
a=a*a%MOD;
b>>=1;
}
return res;
}
inline ll C(int n,int m){
if(n<m) return 0;
return fac[n]*ifac[n-m]%MOD*ifac[m]%MOD;
}
int main(){
scanf("%d%d",&n,&m);
fac[0]=1;
for(int i=1;i<=n;++i) fac[i]=fac[i-1]*i%MOD;
ifac[n]=qpow(fac[n],MOD-2);
for(int i=n-1;~i;--i) ifac[i]=ifac[i+1]*(i+1)%MOD;
scanf("%s%s",s1+1,s2+1);
for(int i=1;i<=n;++i) b[s1[i]-'A'+1]++;
for(int i=1;i<=m;++i) c[s2[i]-'A'+1]++;
dp[0][0]=1;
for(int i=1;i<=26;++i){
sum[0]=dp[i-1][0];
for(int j=1;j<=c[i]-b[i]+min(b[i],c[i+1]);++j)
sum[j]=(sum[j-1]+dp[i-1][j])%MOD;
for(int j=max(0,b[i]-c[i]);j<=min(b[i],c[i+1]);++j)
dp[i][j]=sum[c[i]-b[i]+j]*C(b[i],j)%MOD;
}
ll ans=dp[26][0]*fac[n]%MOD;
for(int i=1;i<=26;++i) ans=ans*qpow(fac[b[i]],MOD-2)%MOD;
printf("%lld\n",ans);
return 0;
}
```