P8518 题解
Undead2008
·
·
题解
题目
题目描述
Khong 阿姨花了 q 天时间准备糖果盒。在第 j 天,对于每个编号满⾜ l[j] \leq k \leq r[j] 的盒⼦ k:
-
如果 v[j] > 0,如果该盒⼦ k 之前已有 p 块糖果,那么在这次操作之后盒⼦将有 \min(c[k], p + v[j]) 块糖果。
-
如果 v[j] < 0,如果该盒⼦之前已有 p 块糖果,那么在这次操作之后盒⼦将有 \max(0, p + v[j]) 块糖果。
你的任务是求出 q 天之后每个盒⼦中糖果的数量。
1\le n,q\le 2\times 10^5
题目分析
以下均用 a 代指原序列。
如果不考虑上下界的话,就是一个朴素的线段树问题。
棘手的是每一个位置都有独特的上界,没办法直接维护。
如果位置 j 在某一时刻的值 a_j=0,就说它碰了下壁;如果位置 j 在某一时刻的值 a_j=c_j,就说它碰了上壁。在最后一次碰壁后,上下界就没有作用了。因此,我们只需要知道最后一次碰壁的时间,就可以很方便地维护答案。
维护“时间”可以离线询问,将每一个操作的贡献打到时间轴上。将不考虑上下界后得到的时间轴记作 b。对于每一个位置 j,如果第 i 个操作将 b_j 加上了 \Delta,就相当于将 b_j 在时刻 i 到时刻 q 内的每一个时刻的值都加上了 \Delta。
建立 n 棵线段树维护每一个位置的时间轴 b 是不现实的。可以使用类似差分的做法,将一个区间操作拆成两个对后缀的操作,即将 (l,r,\Delta) 拆成 (l,n,\Delta) 和 (r+1,n,-\Delta),考虑扫描线思想,用一棵维护时间轴的线段树从左到右扫,到每个位置时都进行该位置上的操作(即到 j 时进行所有 (j,n,\Delta) 操作),这样执行完位置 j 的所有操作后,线段树维护的就是位置 j 的时间轴 b_j。
注意到如果一段时间内 b_j 的极差(最大值减去最小值)大于等于 c_j,则 j 至少碰壁一次。如果在这段时间内的时刻 u 时 b_j 取最大值,时刻 v 时 b_j 取最小值,则在时刻 \max(u,v) 时 j 一定碰壁 ^\dag。不管 \min(u,v) 是否碰壁,\max(u,v) 往上走和往下走都会碰壁。
(蓝线代表考虑上下界后 $b_j$ 的值,红线代表不考虑上下界时 $b_j$ 的值)
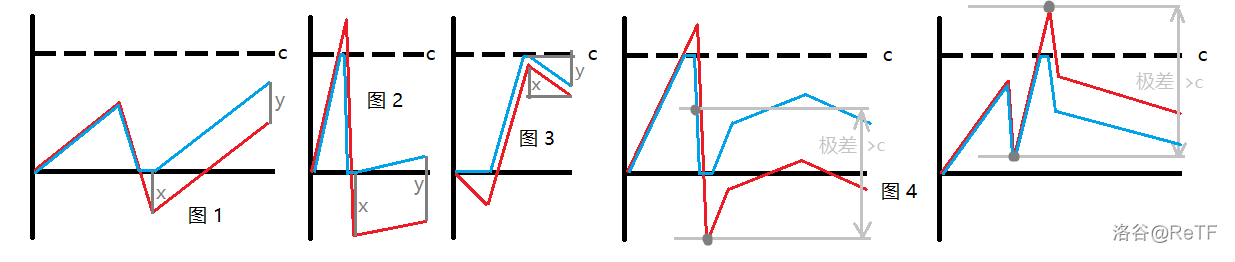
我们要找 $j$ 的最后一次碰壁,也就是要找时间轴上极差 $\ge c_j$ 的最短后缀。线段树的每个节点维护区间最大值,最小值时,这可以在线段树上二分实现。
记时刻 $q$ 时 $b_j$ 的值为 $f$,有三种情况:
- 找不到满足要求的后缀(对应上图 $1$),则答案等于 $f$ 减去整个时间轴每个时刻中 $b_j$ 的最小值。
否则,记 $U$ 和 $V$ 为满足要求的后缀中的最大值和最小值。
- $U$ 比 $V$ 先出现(对应上图 $2$)则答案等于 $f-V$;
- $V$ 比 $U$ 先出现(对应上图 $3$)则答案等于 $c_j-(U-f)$。
注意到前 $3$ 张图上的 $x$ 总等于 $y$,可以根据这个性质推出答案。
这道题就做完了。
### 代码实现
我写了一个带区间操作的线段树,代码或许会长出去好多。
线段树的每个节点维护区间最大值、最小值、懒标记和(叶子结点的)值即可。
[代码](https://www.luogu.com.cn/paste/acdtrv90)