[P4383 : 林克卡特树]

zyc2003 · 2020-11-01 08:23:21 · 题解

Update : 修改了一个有关凸函数定义的大锅 , 感谢评论区的提醒 .

Update : 对 latex 做出了重新完善 (更好的阅读体验) , 增加了感性方面如何认知题目中的凸性 .

题解摘要

详细介绍了题目的转化 , 60 分树上动态规划的做法 , 粗略证明 100 分做法中有关函数的凸的性质的正确性 , 以及二分边界问题 . 不含有 wqs 二分/带权二分/dp 凸优化的引入和介绍 .

题意复述

给定一棵带整数边权的树 , 你一共需要断掉树上的 K 条边 , 然后再重新连接 K 条权值为 0 的边 , 得到一棵新的树 . 最后 , 你选择树上一条路径走过 , 要求最大化权值和 .

转化思路

首先来看 K=0 的情况 . 不用切边 , 意味着我们只需要找到这棵树的最长链即可 . 而 K=1 的话 , 我们枚举切去的一条边 , 变成了两棵树 . 由于新连接的边权值为 0 , 对最终答案没有贡献 , 所以我们应当分别找到两棵树的最长链 , 它们的权值之和即为答案 .

是不是有感觉了 ? 对于 K=2 似乎同理 , 枚举切去的两条边即可 . 而此时我们找到的三条链 , 它们在切去两条边后分属于三棵树 , 是互不相交的 . 这也就意味着 , 如果我们能找到树上的任意三条不相交的链 , 一定可以构造出一种方案 , 使得最终路径经过这三条链和两条新增添的权值为 0 的边 .

那么最终答案显而易见 , 我们找到树上的 K+1 条最大权不相交路径 , 权值之和即为答案 .

分类讨论

求 K+1 条最大权不相交路径 的动态规划做法似乎是一个经典问题 , 我们在这里重新探讨 .

首先考虑一个点的状态 , 它可能并不在一条链上 , 也可能是一条链的某个端点 , 也可能是一条链的中间结点 . 那么自然的想到 , 设 : f[x][j][0/1/2] 表示 : 在以 x 为根的子树内 , 已经有 k 条链 , 且 x 结点 : (并不在链上/是一条链的端点/是一条链的中间结点)

注意这里 "是一条链的中间结点" 的定义 , 并不是意味着 x 是某个从其端点分别是其祖先和其子树中的点的链的中间结点 , 而是一条端点均在其子树内的链的端点 . 姑且设只有一个点的链为 : 退化链吧 .

然后考虑边界状况 . 一个点也可以是一条链 , 这个点既可以当做这条"链"的端点 , 也可以看做这条"链"的中间结点 . 所以 , 我们初始设 :

f[x][0][0]=0

其它所有值设为 -\inf .

先不考虑 x 自成一条链的情况 . 为什么呢 ? 请看下文 .

考虑如何转移 . 我们每处理完一棵子树 , 就立刻进行转移操作 . 设当前处理到的子结点是 y , 从 x 到 y 的边权值为 z:

1. x 并不在链上

貌似很简单的样子 ?

f[x][j][0]=\max(f[x][j][0],f[x][j-k][0]+f[y][k][0]) , j\in [0,K] , k\in[0,j]

不大多对劲 , 子结点 y 的状态其实可以是 1/2 的 , 只要我们 x 不是链的端点就行 . 于是乎我们多设一个状态 : 3 , f[x][j][3]=\max(f[x][j][0,1,2]) 来方便转移 .

于是乎方程变为 :

f[x][j][0]=\max(f[x][j][0],f[x][j-k][0]+f[y][k][3]) , j\in [0,K] , k\in[0,j]

2. x 是一条链的端点

这就有意思了 . x 结点可以在处理到子结点 y 之前就已经是一条链的端点 , 也可以和当前 y 连边成为端点 , 也可以自成一个 退化链 . 这里形成 退化链 很重要 , 它表示新建了一条路径的起始点 , 可能会成为 K+1 条最大不相交路径 的端点之一 .

所以 f[x][j][1],j\in [1,K] 是一下三者取 \max :

\rm A.$ $f[x][j-k][1]+f[y][k][3] , k\in [0,j-1]

\rm B.$ $f[x][j-k][0]+f[y][k][1]+z , k\in [1,j]

\rm C.$ $f[x][j-k-1][0]+f[y][k][3] , k\in [0,j-1] $ $($该方程不会用到$)

3. x 是一条链的中间结点

和 x 是一条链的端点一样 , x 结点可以在处理到子结点 y 之前就已经是一条链的中间结点 , 也可以在处理到子结点 y 之前就是一条链的端点 , 然后和 y 相连 , 成为新的一条链的中间结点 . 当然你也可以自成一个退化链 , 貌似可以看做一个自环 ?

所以 f[x][j][2],j\in [1,K] 是一下三者取 \max :

\rm A.$ $ f[x][j-k][2]+f[y][k][3] , k\in [0,j-1]

\rm B.$ $ f[x][j+1-k][1]+f[y][k][1]+z , k\in [1,j]

\rm C.$ $ f[x][j-k-1][0]+f[y][k][3] , k\in [0,j-1]$ $($该方程不会用到$)

处理完对于所有子结点的 0,1,2 后 , 我们再 :

f[x][j][3]=\max(f[x][j][0],f[x][j][1],f[x][j][2]) , j\in [0,K]

一定要注意 j 和 k 的取值范围 , 以及 j 的倒序循环 , 否则会导致什么你们也知道 (笑

一堆细节

而后我们来讨论转移时的方程之间的位置问题 .

1. 关于为何不一开始就让 x 成为退化链

前面说过 , 我们不考虑在一开始就让 x 自成一条退化链 . 注意到当 x 是一条链的中间结点 , 转移时就可能导致这个退化链和它的子结点相连接 , 使得 x 成为中间结点 . 但是 , 显然此时的 x 是这一整条链的端点 .

2. 注意到 x 为中间结点时有这样的方程 :

\rm B.$ $f[x][j+1-k][1]+f[y][k][1]+z , k\in [1,j]

和别的方程中的 j-k 略有不同 .

这可能会导致重复转移 , 也就是 f[x][j+1-k][1] 已经在本次被更新过 , 而后又用来更新 f[x][j][2] . 所以我们特殊处理 , 在循环 j 时 , 优先处理该情况 .

3. 关于何时让 x 成为退化链

我们也不应该在循环时让 x 成为退化链 , 会导致的情况在 1 时也有说明 . 这就是为什么上面有 "该方程不会用到" . 所以在处理完所有子结点后 , 我们再新建 :

f[x][j][1]=\max(f[x][j][1],f[x][j-1][0])

f[x][j][2]=\max(f[x][j][2],f[x][j-1][0])

时间复杂度是 \mathcal O(nk^2) ... 貌似卡一卡常可以通过 k\leq 100 , 但是我没卡成 ... 吸氧才能过 60 分 .

void dfs(int x,int fa) {
    f[x][0][0]=0;
    for(int i=head[x];i;i=nxt[i]) {
        int y=ver[i],z=edge[i];
        if(y == fa) continue;
        dfs(y,x);
        // j in [K,1]
        for(int j=K;j>=1;j--) {         
            //特殊处理 
            for(int k=j;k>=1;k--)
                f[x][j][2]=max(f[x][j][2],
                max(f[x][j-k][2]+f[y][k][3],f[x][j+1-k][1]+f[y][k][1]+z)
                ); 
            //k is j
            f[x][j][0]=max(f[x][j][0],f[x][j-j][0]+f[y][j][3]);  //有意义
            f[x][j][1]=max(f[x][j][1],f[x][j-j][0]+f[y][j][1]+z);//有意义

            //k in [j-1,1]
            for(int k=j-1;k>=1;k--) {
                f[x][j][0]=max(f[x][j][0],f[x][j-k][0]+f[y][k][3]);             
                f[x][j][1]=max(f[x][j][1],
                max(f[x][j-k][1]+f[y][k][3],f[x][j-k][0]+f[y][k][1]+z)
                );
            }
            //k is 0
            f[x][j][0]=max(f[x][j][0],f[x][j-0][0]+f[y][0][3]);  //无意义 
            f[x][j][1]=max(f[x][j][1],f[x][j-0][1]+f[y][0][3]);  //无意义
            f[x][j][2]=max(f[x][j][2],f[x][j-0][2]+f[y][0][3]);  //无意义  
        } 
        //j is 0
        //f[x][0][0]=... 无意义 , 早就被算过了 
    }
    for(int j=1;j<=K;j++)
        f[x][j][1]=max(f[x][j][1],f[x][j-1][0]),
        f[x][j][2]=max(f[x][j][2],f[x][j-1][0]);
    for(int j=0;j<=K;j++)
        f[x][j][3]=max(f[x][j][0],max(f[x][j][1],f[x][j][2])); 

}

优化策略 : 凸优化

这个函数是凸的 ! --- 众大佬

啥呀 , 啥函数啊 , 为啥是凸的啊 ...

如果我们以不相交路径数 K 为横坐标 , K 条不相交路径最大权值和为 f(K) 为纵坐标 , 那么这个函数就是凸函数 ! (注意这里的 K 实际上等于题目给的 K+1 )

啥是凸函数 ... 为啥能证明是凸函数呢 ?

"凸函数"的定义 , 在别的题解有详细解释 , 我就不再叙述了 . 这里着重感性证明该函数为凸的理由 . (不考虑特殊构造情况 , 例如边权全部相等之类的)

感性理解

经过了近一年的学习 (现在为 21 年的 7 月 , 离发布这篇题解的 20 年 11 月已经过去了快一年) , 我回顾本题 , 发现 ... 这不显然是凸优化 ? ~~(我已经成为当年自己口中的大佬了吗 qaq)~~

具体的说 , 能看出凸优化 , 是因为有恰好 K 条的限制 , 这是 wqs二分优化 dp 的重要标志 ; 当 K 较小时 , 随着 K 的不断增大 , 我们能选的路径越来越多 , 值 f(K) 越来越大 , 但是增长的速度不断变慢 (能选的权值大的路径在一开始 K 较小就被选了 , 后面能选的边权越来越小) ; 而到了某个临界 , 即 K 较大的时候 , 由于要满足路径不相交 , 很多本来可以选的边被舍弃 , 我们此时的 f(K) 也越来越小 , 且减少的速度不断增大 (能断掉的权值小的边在之前就被断掉了 , 后面只能选择权值大的边切断) .

所以 , 凸优化的重要性质是 , 总有某个限制 (比如恰好啥啥啥的) , 让你在该限制较小时能轻易得到大的答案 , 但是限制较大时迫不得已减小答案 .

理性证明

实际上 , 只要证明任意一个 K 满足 f(K+1)-f(K)\geq f(K+2)-f(K+1) 即可 (非严格凸) .

首先来考虑 K=1 的情况 , 求出树的直径即可 .

那么 K=2 呢 ? 我们考虑这两条路径和树的直径有什么关系 :

不会是最优解 . 由于**直径**是树上最长链 , 我只需要把其中一条路径变为直径 , 得到的权值和一定更大 . $2.$ 两条路径有一条和直径相交 , 但是直径上的两个端点不都在这两条路径上和 $1$ 类似 , 将这条与直径相交的路径换为直径 , 权值和更大 . $3.$ 两条路径有一条和直径相交 , 但是直径上的两个端点都在这两条路径上可以是最优解 . $4.$ 两条路径都与直径相交 , 但是并不是直径上所有点都包括在这两条路径上考虑其中一条路径 , 它被分成三部分 , 有两部分不在直径上 , 设为 $\rm Left$ 和 $\rm Right$ . 有一部分在直径上 , 设为 $\rm Mid$ 部分 . 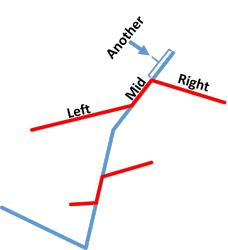请看图 : ![](https://cdn.luogu.com.cn/upload/image_hosting/qhmyf9pa.png?x-oss-process=image/resize,m_lfit,h_250,w_300) 还有一个 $\rm Another$ 部分 , 是直径的一部分 . 设 $\rm val(path)$ 表示路径 $\rm path$ 的权值和 . 一定有 : $\rm val(Another) \geq val(Right)$ . (直径的定义) 所以 , 将 $\rm Right$ 部分换为 $\rm Another$ 更优 . 可以证明 , 直径的两个端点一定在新的两条路径上 . $5.$ 两条路径都与直径相交 , 但是直径上所有点都包括在这两条路径上可以是最优解 . 于是我们发现 , 最优解一定包括直径的两个端点 . 可以类推 , 从 $K$ 到 $K+1$ , 前 $K$ 条不相交路径的端点一定被包括在内 . 所以 , 找到新一条路径的过程可以具体化为这样 : 要么我们重新在树中找到一条路径 , 设为 $\rm A$ 操作 ; 要么我们将一条路径拆开 , 两个端点分离 , 各自作为两条新路径的端点 , 设为 $\rm B$ 操作 . 由此 , 从 $K$ 到 $K+1$ 到 $K+2$ 的最优解的变化一定是如下构造之一 : $1.$ $\rm A,A

2.$ $\rm A,B

3.$ $\rm B,A

4.$ $\rm B,B

我们设 \Delta f(K)=f(K+1)-f(K) . 下面主要使用反证法证明 .

如果两次操作中 , 我们都不是针对同一条链 ; 且有 : \Delta f(K+1) > \Delta f(K)

说明第二次操作新增的贡献和比第一次的大 , 那么为什么不第一次就进行这个操作呢 ? 所以在该类操作中 , 一定满足 \Delta f(K+1) \leq \Delta f(K) .

如果针对的是同一条链 , 那就只有 \rm A,B 和 \rm B,B 两种符合 . 且看图片演示 :

对于 \rm B,B 而言 :

那么最优解中 , 我们应当第一次就执行现在执行的第二次操作 , 以使得权值和最大化 .

对于 \rm A,B 而言 :

这也是不对的 , 因为移项后 :

显然我们最优解中 , 第一次操作时应当选择加入第二次操作时分化得到的两条链中权值和最大那条 , 一定比现在第一次操作优 .

于是乎 , 我们就证明了 f(K) 函数是凸的 . 这样就可以愉快地使用 wqs 二分/带权二分/dp 凸优化了 !

凸壳特殊问题

wqs 二分/带权二分/dp 凸优化在别的题解讲解得十分清楚 , 不再赘述使用方法和新的树上 dp 方程的写法(使用结构体和重载运算符) .

但是有一点需要注意 , 如果这个"凸"是不严格的 , 也就是我们要求的 K , 其实是 : (K,f(K)),(K+1,f(K+1)),(K+2,f(K+2)) 多点共线怎么办 ?

这里需要稍微处理一下 , 设我们最终的斜率为 ans . 那么我们输出的答案不应该是 :

不相交链最大权值和 - ans\ * \ 不相交链条数

而应该是 :

不相交链最大权值和 - ans\ * \ K

否则会导致答案错误 . 可以使用 \rm loj 的这组数据试试 :

至于为什么 ? 如果你熟悉 wqs 二分的本质 , 能很快能想出答案 . 如果不熟悉 , 请再仔细瞧瞧 wqs 二分哦 !

(p.s. : 答案可见评论区大佬发言)