整体二分--题解 P3242 【[HNOI2015]接水果】
Vocalise
·
·
题解
挺毒的一道题。
首先还是要说说如何将问题转化的,即如何考虑路径之间的包含关系。
我们有 DFS 序:入序 ln_x 及出序 rn_x=ln_x+size_x-1。
设有 ln_x < ln_y,ln_v < ln_u,路径 (x,y) 包含 (v,u)。
讨论 (v,u) 路径的形态。
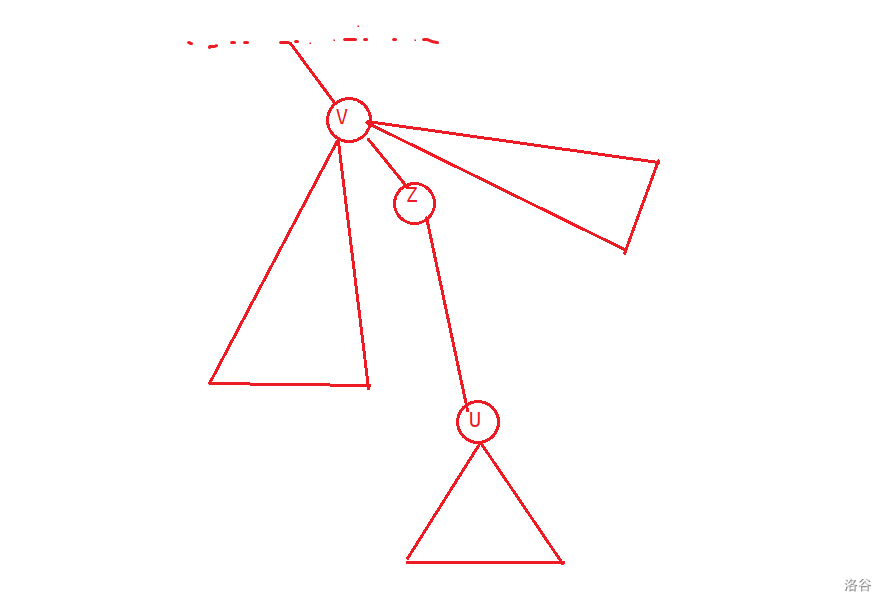
考虑 $z$ 为 $(v,u)$ 路径上距离 $v$ 最近的点,发现 $(x,y)$ 一个在 $z$ 的子树之外,一个在 $u$ 的子树之内。求 $z$ 可以倍增或树剖随便。
前者的 $ln$ 区间为 $[1,ln_z)\cup(rn_z,n]$,而后者为 $[ln_u,rn_u]$。
于是 $x$ 就是前者, $y$ 就是后者吗?也不尽然。
如果 $ln_z > 1$,则 $x\in[1,ln_z)$, $y\in[ln_u,rn_u]$ 时包含;
同时如果 $rn_z < n$,则 $x\in[ln_u,rn_u]$,$y\in(rn_z,n]$ 时包含。
发现两种情况没有交集,看作两个条件即可。
---
$u$ 和 $v$ 互不为祖先。
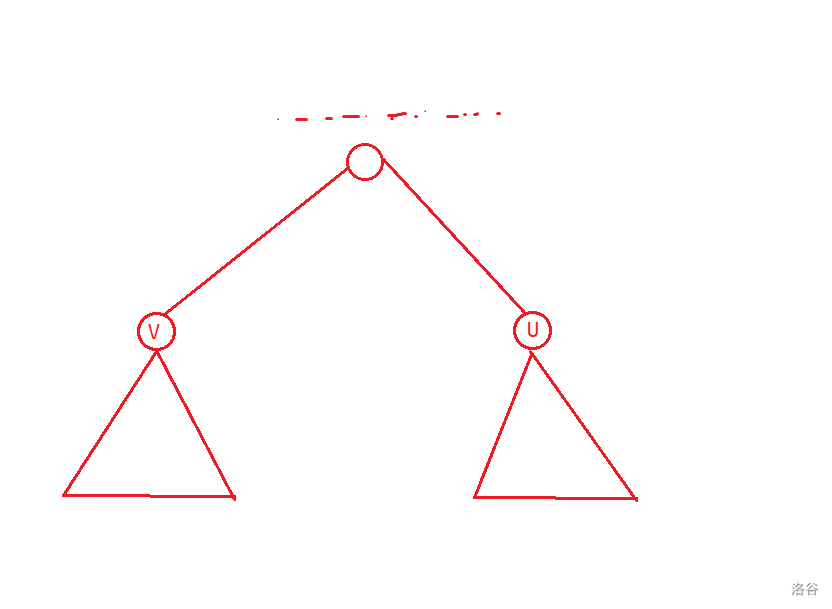
这种情况就是 $x,y$ 分别在 $v,u$ 子树中了。即:$x\in[ln_v,rn_v],y\in[ln_u,rn_u]$。
---
发现对于每个条件, $x$ 和 $y$ 都属于一个区间,即对于一个点 $(x,y)$,它在一个矩形中时,这条路径 $(x,y)$ 被该路径包含。
问题变为:求若干点包含其的权值 $k$ 大矩形。
考虑一个弱化问题:求若干点包含其的矩形数。
自然问矩形包含的点数我们知道怎么求:把一个坐标轴变为时间轴,矩形拆成 $4$ 个前缀,扫描线顺序插入,维护树状数组即可。
事实上这个问题也可以这么做。树状数组单点加区间查改成区间加单点查即可,具体地:
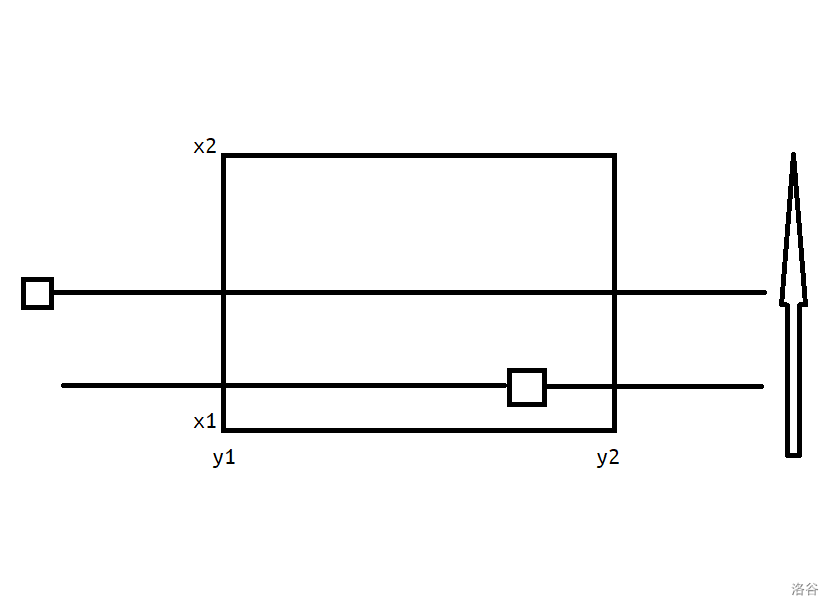
从下往上扫,到 $x1$ 位置时在 $[y1,y2]$ 上加一,到询问点时查询其横坐标上的值,到 $x2 + 1$ 时在 $[y1,y2]$ 上减一。
这个问题带上 $k$ 大且可以离线,整体二分。
在二分里不用排序,之前按 $y$ 坐标第一,修改在前第二排好序;树状数组维护 $x$ 坐标轴;二分本身维护权值轴。
整体二分本身是模板,可以去其它题目如 [P3332 [ZJOI2013]K大数查询](https://www.luogu.com.cn/problem/P3332) 看看。
求包含数的子问题是 $O(n\log n)$ 的,套上整体二分,总复杂度是 $O(n\log^2n)$ 的。
> 注意:
1. $(x,y)$ 和 $(v,u)$ 都是有序的;
3. 操作中直接存矩形的边界线即可;
2. $y$ 坐标相同时,修改应该在前;
4. 操作数组的空间较大。
```cpp
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
const int MAXN = 50001;
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch > '9' || ch < '0') { if(ch == '-') f = -1; ch = getchar(); }
do x = x * 10 + ch - 48, ch = getchar(); while(ch >= '0' && ch <= '9');
return x * f;
}
struct Edge {
int u; Edge *nxt;
} *adj[MAXN];
void ins(int v,int u) {
Edge *e = new Edge; e -> u = u;
e -> nxt = adj[v], adj[v] = e;
}
int fa[MAXN],d[MAXN],sv[MAXN],son[MAXN],top[MAXN];
int ln[MAXN],rn[MAXN],dfn;
void Dfs1(int v,int f) {
ln[v] = ++dfn;
fa[v] = f, d[v] = d[f] + 1, sv[v] = 1;
for(Edge *i = adj[v];i;i = i -> nxt) {
int u = i -> u;
if(u == f) continue;
Dfs1(u,v);
sv[v] += sv[u]; if(sv[u] > sv[son[v]]) son[v] = u;
}
rn[v] = dfn;
}
void Dfs2(int v,int t) {
top[v] = t;
if(!son[v]) return;
Dfs2(son[v],t);
for(Edge *i = adj[v];i;i = i -> nxt) {
int u = i -> u;
if(top[u]) continue;
Dfs2(u,u);
}
}
int GetSon(int v,int u) {
while(top[v] != top[u]) {
if(fa[top[v]] == u) return top[v];
v = fa[top[v]];
}
return son[u];
}
struct Item {
int tp,y,l,r,k,id;
Item() {}
Item(int _tp,int _y,int _l,int _r,int _k,int _id) :
tp(_tp), y(_y), l(_l), r(_r), k(_k), id(_id) {}
friend bool operator <(const Item &x,const Item &y) {
if(x.y != y.y) return x.y < y.y;
else return x.tp < y.tp;
}
} p[MAXN * 4], p1[MAXN * 4], p2[MAXN * 4];
int n,m,q,b[MAXN],ans[MAXN],f[MAXN];
void Add(int i,int x) {
for(;i <= n;i += i & (-i))
f[i] += x;
}
int Sum(int i) {
int ans = 0;
for(;i;i -= i & (-i)) ans += f[i];
return ans;
}
void Solve(int l,int r,int L,int R) {
if(L > R) return;
if(l == r) {
for(int i = L;i <= R;i++)
if(p[i].tp) ans[p[i].id] = l;
return;
}
int m = (l + r) >> 1, c1 = 0, c2 = 0;
for(int i = L;i <= R;i++) if(!p[i].tp) {
if(p[i].k <= m) Add(p[i].l,p[i].id), Add(p[i].r + 1,-p[i].id), p1[++c1] = p[i];
else p2[++c2] = p[i];
} else {
int s = Sum(p[i].l);
if(s >= p[i].k) p1[++c1] = p[i];
else p[i].k -= s, p2[++c2] = p[i];
}
for(int i = 1;i <= c1;i++) p[L + i - 1] = p1[i];
for(int i = 1;i <= c2;i++) p[R - c2 + i] = p2[i];
Solve(l,m,L,L + c1 - 1), Solve(m + 1,r,L + c1,R);
return;
}
int main() {
n = read(), m = read(), q = read();
for(int i = 2;i <= n;i++) {
int v = read(), u = read();
ins(v,u), ins(u,v);
}
Dfs1(1,1), Dfs2(1,1);
int t = 0;
for(int i = 1;i <= m;i++) {
int v = read(), u = read(), k = b[i] = read();
if(ln[v] > ln[u]) std::swap(v,u);
if(rn[v] >= rn[u]) {
v = GetSon(u,v);
if(ln[v] > 1) {
p[++t] = Item(0,ln[u],1,ln[v] - 1,k,1);
p[++t] = Item(0,rn[u] + 1,1,ln[v] - 1,k,-1);
}
if(rn[v] < n) {
p[++t] = Item(0,rn[v] + 1,ln[u],rn[u],k,1);
p[++t] = Item(0,n + 1,ln[u],rn[u],k,-1);
}
} else {
p[++t] = Item(0,ln[u],ln[v],rn[v],k,1);
p[++t] = Item(0,rn[u] + 1,ln[v],rn[v],k,-1);
}
}
std::sort(b + 1,b + 1 + m);
int tmp = std::unique(b + 1,b + 1 + m) - b - 1;
for(int i = 1;i <= t;i++) p[i].k = std::lower_bound(b + 1,b + 1 + tmp,p[i].k) - b;
for(int i = 1;i <= q;i++) {
int v = read(), u = read(), k = read();
if(ln[v] > ln[u]) std::swap(v,u);
p[++t] = Item(1,ln[u],ln[v],0,k,i);
}
std::sort(p + 1,p + 1 + t);
// for(int i = 1;i <= t;i++) std::printf("i=%d tp=%d y=%d l=%d r=%d k=%d id=%d\n",i,p[i].tp,p[i].y,p[i].l,p[i].r,p[i].k,p[i].id);
Solve(1,tmp,1,t);
for(int i = 1;i <= q;i++) std::printf("%d\n",b[ans[i]]);
return 0;
}
```
同样有不用整体二分的做法。扫描线的同时,权值线段树套动态开点线段树区间加,单点查即可。空间 $O(n\log^2 n)$ 时间 $O(n\log^2n)$。