P12650 [KOI 2024 Round 2] 双 v 字形涂色
_JF_
·
·
题解
Link
压力!
好难写的模拟/tuu,思路还行。
分类讨论两个 V 是否相交,只会相交,不相交看了尺子姐姐的题解才会呜呜呜。
第一种是形如样例,给出的近似 W 的形状,我们不妨考虑枚举中间的那个顶端,思考两边的最值怎么取。
来看右边怎么取,实际上是这样的一个问题:
对于 (i,j),(i+1,j+1),\dots(i+x,j+x) 这一段连续的白色格子,定义 g_{i,j} 为每个白色格子往右上延续的长的白格数量,定义 f_{i,j}=\max_{i+x\le n,j+x\le m }{g_{i+x,j+x}+x}。
很经典的问题了吧,这个东西是有单调性的。
对于两个位置 $(i+x,j+x)$ 和 $(i+x',j+x')$ 而言 $(x'>x)$,$(i,j)\rightarrow (i+x-1,j+x-1)$ 这一段贡献是一样的,那我们只用把 $(i+x',j+x')$ 平移到 $(i+x,j+x)$,比较谁更优即可。
~~这个人一开始用 deque 维护,但是 $9\times 10^6$ 个~~,用 vector 维护即可。
对于左半部分的处理是类似的。
还有一种相交情况形如:
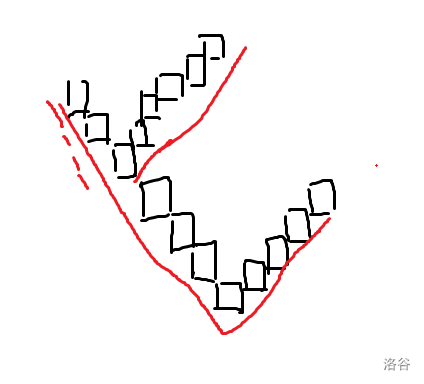
这个是好处理的,直接维护前缀 $\max$ 即可。
- 不相交的情况。
观察奇偶性,发现若 $(i,j),(i-1,j-1),(i-1,j+1)\dots$ 为白色,那么这些点坐标和的奇偶性不变。
那么可以枚举 `V` 底端那个点,两个点奇偶性不一样,说明必然不相交。
还有一种情况是包含,这种就考虑一个 $B_{i,j}$ 表示以 $(i,j)$ 为底部点,能完全包含最大的 `V` 的格子数量,递推式显然:
$$B_{i,j}=\max\{B_{i-1,j},B_{i-1,j-1},B_{i-1,j+1},val_{i,j}\}$$
其中 $val_{i,j}$ 表示当前点为底部点能最大构成 `V` 的格子数。
最后一种情况,就是注意到构成 `V` 的所有点坐标,右边的边的 $i+j$ 是定值,左边的边 $i-j$ 是定值,那么分别以两种情况作为分割线,分左右统计即可。
难写到爆炸。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N =3001;
char ch[N][N];
struct node{
int i,j,val;
};
vector<node> q[9000001];
int predis1[N<<1],predis[N<<1],sum1[N][N],sum2[N][N],tot,LU_Mx[N][N],RU_Mx[N][N],id[N][N][2];
int num1,num2,ans,n,m,RU[N][N],LU[N][N],Now[N][N],B[N][N];
int main(){
// freopen("P12650_36.in","r",stdin);
cin>>n>>m;
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>ch[i][j];
// 1,2
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
RU[i][j]=RU[i-1][j+1]+1,LU[i][j]=LU[i-1][j-1]+1,Now[i][j]=RU[i][j]+LU[i][j]-1;
if((i+j)%2==0) num1=max(num1,Now[i][j]); else num2=max(num2,Now[i][j]);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
B[i][j]=max(max(B[i-1][j],max(B[i-1][j-1],B[i-1][j+1])),Now[i][j]);
ans=max(ans,B[i-1][j]+Now[i][j]);
}
// cout<<B[3][1]<<endl;
ans=max(ans,num1+num2);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) predis[i+j]=max(predis[i+j],Now[i][j]),predis1[i-j+m]=max(predis1[i-j+m],Now[i][j]);
for(int i=1;i<=n+m;i++) predis[i]=max(predis[i],predis[i-1]);
for(int i=1;i<=n+m-1;i++) predis1[i]=max(predis1[i],predis1[i-1]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
int now=i+j-LU[i][j]*2;
ans=max(ans,Now[i][j]+predis[now]);
int now1=i-j+m-2*RU[i][j];
ans=max(ans,Now[i][j]+predis1[now1]);
}
// 3
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
RU_Mx[i][j]=max(RU_Mx[i-1][j-1],RU[i][j]),LU_Mx[i][j]=max(LU_Mx[i-1][j+1],LU[i][j]);
ans=max(ans,RU_Mx[i-1][j-1]-1+Now[i][j]);
ans=max(ans,LU_Mx[i-1][j+1]-1+Now[i][j]);
}
// 4 RU:1 LU:0
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
// LU
if(ch[i-1][j-1]=='1'){
int now=id[i-1][j-1][0];
while(!q[now].empty()&&RU[i][j]+(i-q[now].back().i)>=q[now].back().val) q[now].pop_back();
q[now].push_back({i,j,RU[i][j]}),id[i][j][0]=id[i-1][j-1][0];
}
else id[i][j][0]=++tot;
// RU
if(ch[i-1][j+1]=='1'){
int now=id[i-1][j+1][1];
while(!q[now].empty()&&LU[i][j]+(i-q[now].back().i)>=q[now].back().val) q[now].pop_back();
q[now].push_back({i,j,LU[i][j]}),id[i][j][1]=id[i-1][j+1][1];
}
else id[i][j][1]=++tot;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
if(ch[i-1][j-1]=='0'||(i-1<1)||(j-1<1)){
int now=id[i][j][0],lsti=i,lstj=j;
for(int l=0;l<q[now].size();l++){
int nowi=q[now][l].i,nowj=q[now][l].j;
while(lsti<nowi){
sum1[lsti][lstj]=Now[nowi][nowj]-LU[lsti-1][lstj-1];
// cout<<"0"<<' '<<lsti<<' '<<lstj<<' '<<sum1[lsti][lstj]<<endl;
lsti++,lstj++;
}
}
}
if(ch[i-1][j+1]=='0'||(i-1<1)||(j+1>m)){
int now=id[i][j][1],lsti=i,lstj=j;
for(int l=0;l<q[now].size();l++){
int nowi=q[now][l].i,nowj=q[now][l].j;
while(lsti<nowi){
sum2[lsti][lstj]=Now[nowi][nowj]-RU[lsti-1][lstj+1];
// cout<<"1"<<' '<<lsti<<' '<<lstj<<' '<<sum2[lsti][lstj]<<endl;
lsti++,lstj--;
}
}
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if(ch[i][j]=='0') continue;
ans=max(ans,sum1[i][j]+sum2[i][j]-1+max(LU[i][j],RU[i][j])-1);
// if(ans==36) cout<<i<<' '<<j<<' '<<sum1[i][j]<<' '<<sum2[i][j]<<endl,exit(0);
}
// cout<<sum1[3][7]<<' '<<sum2[3][7]<<endl;
cout<<ans<<endl;
return 0;
}
/*
5 5
10101
01010
00100
01010
10101
*/
```