P1248 加工生产调度 题解
SMT0x400
·
·
题解
补一个第一篇题解的证明。
拿出原来的排序不等式的式子。需要让最终序列满足:
我们分析一下,因为依旧是四个元素两两之间最小值的东西,不好求。
这里就分析 $\min(a_1,b_2)\le \min(a_2,b_1)$ 好了。
需要分类讨论。
首先可以尝试画拓扑图来解决问题。研究同一个变量 $a,b$ 之间的关系。
+ 一,$a_1<b_1,a_2<b_2$ 时候,如下图所示,我们要求 $a_1$ 为最小值(因为这种情况下 $b_2$ 不可能为最小值),就是需要在拓扑图上连接一条边使得 $a_1$ 是拓扑图的起点。
+ 则可以如下图红色、蓝色所示方式连边。最本质的答案就是需要保证 $a_1\le a_2$。

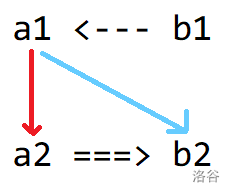
+ 二,讨论 $a_1<b_1,a_2\ge b_2$ 的情况。如图所示,要求 $a_1$ 为最小值。
+ 则需要保证 $a_1\le b_2$。
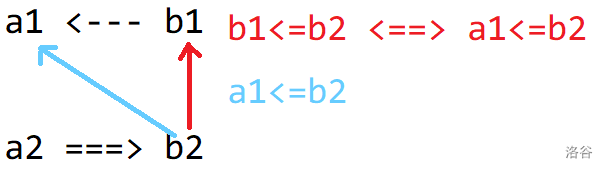
+ 这种情况下 $b_2$ 可能为最小值,那么就是上图这样:本质是 $a_1\ge b_2$ 时候才会出现。
+ 所以 $a_1<b_1,a_2\ge b_2$ 的情况,无论 $a_1$ 和 $b_2$ 的大小关系如何,都能够成立。
+ 三,当 $a_1=b_1$ 且 $a_2<b_2$ 时候,只能让 $a_1$ 为最小值,这个时候,就需要 $a_1\le a_2$ 时候 $a_1$ 才有可能为最小值了。
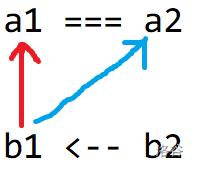
+ 四,当 $a_1=b_1$ 且 $a_2=b_2$ 时候,这时怎么排序都没有影响了,因为等号一定成立。
+ 五,当 $a_1=b_1$ 且 $a_2>b_2$ 时候,当 $a_1$ 为最小值时,如下图所示,这时要想小于等于号成立,就得 $b1\le b2$。
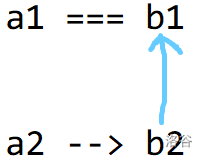
+ 当 $b_2$ 为最小值时,就有 $b_1\ge b_2$ 了。(图未画出)
+ 六,当 $a_1>b_1$ 且 $a_2\le b_2$ 时候,$a_1$ 取不到最小值,$b_2$ 可能取到全局最小值,所以当小于等于号成立时候,必有 $a_2=b_2$ ,且满足 $b_1\le a_2$。如下图所示。实际上,原式恒成立。

+ 七,当 $a_1>b_1$ 且 $a_2>b_2$ 时候,只有 $b_2$ 才有可能取到最小值,则有 $b_1\ge b_2$。

+ 总结上述七种情况:
+ 当 $a_1<b_1$ 时候,如果 $a_2<b_2$ 则应该有 $a_1\le a_2$;如果 $a_2\ge b_2$ 则原式恒成立;
+ 当 $a_1=b_1$ 时候,如果 $a_2<b_2$ 则应该有 $a_1\le a_2$;如果 $a_2=b_2$ 则原式恒成立;如果 $a_2>b_2$ 则有 $b_1\le b_2$。
+ 当 $a_1>b_1$ 时候,如果 $a_2\le b_2$ 则原式恒成立;如果 $a_2>b_2$ 则有 $b_1\ge b_2$。
具体写程序的时候,可以设置 $d$ 表示 $a$ 与 $b$ 的大小关系来实现。
```cpp
struct nd{
I a,b,d,id;
friend bool operator <(nd x,nd y){
if(y.d==x.d){
if(x.d<0)return x.a<y.a;
if(x.d==0)return x.id<y.id;
return x.b>y.b;
}return x.d<y.d;
}
}
```