题解 P5959 【 [POI2018]Plan metra】
maruize
·
·
题解
少有的构造题
我们可以想象这样一个形状:
(一条线上挂一堆点)
(图画的不好)
首先考虑在线上的点
要想知道哪些点在线上,只要知道1-n的距离
显然他是
min_{i=1}^n(d(1,i)+d(i,n))
因为如果d(1,n)比这个长的话 d(1,i)+d(i,n)<d(1,n)的点将无处安放。
然后考虑剩下的点能不能挂上
M=d(t,i),X=d(1,t),Y=d(t,n)
如图,若点i能挂在位置为t的点,则
A=X+M(1),B=Y+M(2)
所以判断一个点i是否能挂在线上,只要判断是否有在线上的点j使
$d(1,i)-d(i,n)=d(1,j)-d(j,n)$。
开个桶存一下即可。
code:
```cpp
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
int n;
void WA(){puts("NIE"),exit(0);}
struct data{int x,y,id;}f[500005];
bool cmp(data a,data b)
{return a.x+a.y==b.x+b.y?a.x<b.x:a.x+a.y<b.x+b.y;}
bool CMP(data a,data b){return a.x<b.x;}
int ope[10000005],*val=ope+5000000;//桶
//要开够,要不RE|WA|UKE。。。
int fa[500005],v[500005];
signed main(){
int M=0x3f3f3f3f;
scanf("%d",&n);//cout<<n<<endl;
for(int i=1;i<=n;i++)f[i].id=i;
for(int i=2;i<n;i++)scanf("%d",&f[i].x);
for(int i=2;i<n;i++)scanf("%d",&f[i].y);
for(int i=2;i<n;i++)M=min(M,f[i].x+f[i].y);
f[1]={0,M,1},f[n]={M,0,n};
sort(f+1,f+n+1,cmp);//排序来分隔在线上的和不在的。
int s;
val[-M]=1;//往桶里塞进d(1,1)-d(1,n)
for(s=2;s<=n;s++){
if(f[s].x+f[s].y==M){//在线上
if(f[s].x==f[s-1].x)WA();//点间距离!=0
val[f[s].x-f[s].y]=s;
//往桶里塞进d(1,s)-d(s,n)
}
else break;//不在
}
for(int i=s;i<=n;i++){
int&t=val[f[i].x-f[i].y];
if(t)fa[i]=t,v[i]=f[i].x-f[t].x;
else WA();
}
puts("TAK");
for(int i=2;i<s;i++)
printf("%d %d %d\n",f[i-1].id,f[i].id,f[i].x-f[i-1].x);
for(int i=s;i<=n;i++)
printf("%d %d %d\n",f[fa[i]].id,f[i].id,v[i]);
return 0;
}
```
结束?
---
然后你光荣的得了80pts。
这是漏了一种情况:
1-n的路径上没有其他点
like this:
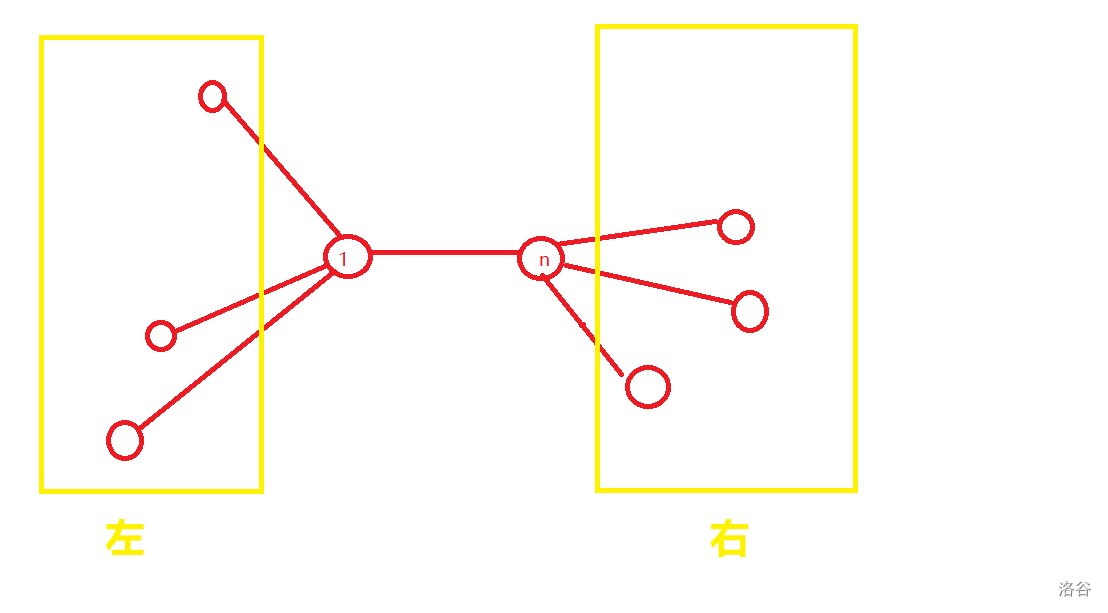
这时d(1,n)就不是原来的了。
d(1,n)=
$ \ $d(1,i)-d(i,n)$ \ $[ i在“左侧” ]
$ \ $d(i,n)-d(1,i)$ \ $[ i在“右侧” ]
只有对于所有的i,d(1,n)相等才可以。
所以特判一下:
```cpp
bool flag=1;
for(int i=3;i<n;i++)if(abs(f[i].x-f[i].y)!=abs(f[2].x-f[2].y))flag=0;
if(!flag)return;
int M=abs(f[2].x-f[2].y);//M=d(1,n)
if(M==0)return;
puts("TAK");
printf("1 %d %d\n",n,M);
for(int i=2;i<n;i++){
//if(f[i].x==f[i].y)return;
if(f[i].x<f[i].y)printf("1 %d %d\n",i,f[i].x);
else printf("%d %d %d\n",i,n,f[i].y);
}exit(0);
```