P1761 正方形 题解
jzzcjb
·
·
题解
今天把这道题刚过去了,写篇题解纪念一下。
发现因为数据水,所以有些并没有考虑全情况的代码也AC了。
我的方法比较容易懂。写一篇自认为正确的题解,有错轻喷。
Step 0
先看懂题意,题目中的从上往下看是指把纸竖过来,从y轴正方向的位置往下看,所有的正方形都变成了一段段线段,其中有多少个正方形(变成的线段)能被看到。原来的这4个正方形从上面看是这样的,
对齐之后
黄色的那一小段 1 就被左边的 5 和右边的 4 盖住了,所以输出 1,2,4 。
依次 就是不能越过上一个正方形。就像样例中的 3 没有插到 1,2 中间的空的意思。这意味着,一旦给定每个正方形的边长,那么它们的放置情况就是一定的了。
这给了我们思路,可以依次把这 n 个矩形都放置好,再计算那些能被看到,那些不能被看到。
Step 1
计算每个正方形应该被放到哪。
首先转化一下:
所以不妨重新定义每个正方形对角线的长度为“边长”,并且以相同的刻度对 x 轴的刻度进行重置。就像这样
回到我们的要求:看看两个正方形相邻都有哪些形态
不难发现,两个正方形相邻的时候,只要让其中比较小的那个有一个“落脚点”即可。也就是说,只要它们之间的距离等于两者边长的较小值即可。
所以得出递推式
pos_i=pos_{i-1}+\min(a_i,a_{i-1})
这样就结束了吗?考虑这样一种情况
如果按上面的公式计算,就变成了
显然不对。所以,我们还要满足对于之前所有的正方形,都能让它满足存在“落脚点”,即
pos_i=\max_{j=1}^{i-1} \{ pos_j+\min(a_i,a_j) \}
这样,就求了每个正方形的位置。
Step 2
计算正方形覆盖
根据对于边长的重新定义,很容易能写出一个正方形的左右两个顶点的位置 pos_i+\frac{a_i}{2} 和 pos_i-\frac{a_i}{2}。
最简单的想法是如果它左边的正方形完全覆盖它,或者它右边的正方形完全覆盖它,或者两边一边覆盖一半,那么它就不会被看见了。
pos_{i-1}+\frac{a_{i-1}}{2}>pos_i+\frac{a_i}{2}
pos_{i+1}-\frac{a_{i+1}}{2}<pos_i-\frac{a_i}{2}
pos_{i-1}+\frac{a_{i-1}}{2}>pos_{i+1}-\frac{a_{i+1}}{2}
但是,有这样一种情况。
$$L_i=\min_{j=i+1}^{n} \{ pos_j-\frac{a_j}{2}\}$$
$$R_i=\max_{j=1}^{i-1} \{ pos_j+\frac{a_j}{2}\}$$
如果两个端点接触了,则证明这个正方形被覆盖了。
$L_i$要与 $pos_i+\frac{a_i}{2}$ 取 $\min$ , $R_i$要与 $pos_i-\frac{a_i}{2}$ 取 $\max$。因为即使没有接上另一头,被一边单独覆盖也是不行的。
这样就结束了吗?再看一个反例
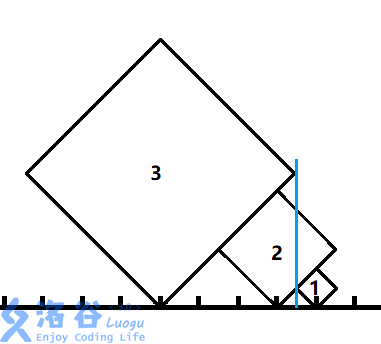
这里$L_2$ $R_2$很显然已经接触了,但还是能看到 $2$ 。因为 $3$ 在 $2$ 的下面,所以即使 $3$ 接触了 $2$ 的右警戒线,但还是对 $2$ 造不成威胁。所以计算 $L $ 和 $R$ 时要忽略那些比 $i$ 矮的,也就是边长小与 $i$ 的正方形。
还有注意 $L $ 和 $R$ 的初始化,一个要赋成极大值,一个要赋成极小值,不能赋成 $0$ 。因为有可能某个正方形的左顶点会变为负数,这样就影响了它左边的某些正方形。
这样,这道题就被完美解决了,细节比较多,但代码很简单。
**代码:**
```
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,a[101],p[101],R[101],L[101];//p -> pos
int main(){
while(cin>>n&&n){
memset(p,0,sizeof(p));
memset(a,0,sizeof(a));
memset(L,0x3f,sizeof(L));
memset(R,0xcf,sizeof(R));
for(int i=1;i<=n;i++){
cin>>a[i];a[i]*=2;//后面有/2操作,这里要*2以逃避double
for(int j=1;j<i;j++)
p[i]=max(p[i],p[j]+min(a[j],a[i]));
}
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++)if(a[j]>a[i])
R[i]=max(R[i],p[j]+a[j]/2);
R[i]=max(R[i],p[i]-a[i]/2);
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++)if(a[j]>a[i])
L[i]=min(L[i],p[j]-a[j]/2);
L[i]=min(L[i],p[i]+a[i]/2);
}
for(int i=1;i<=n;i++)
if(R[i]<L[i]) cout<<i<<" ";
puts("");
}
}
```
另外再附上刚才举反例的数据
```
3
7 3 1
1 2
```