动态维护单调栈的一种方法
zjc5
·
·
算法·理论
前言:
本人没有见过需要此算法的题目,所以文中的题目均没有来源。
感谢 xzf_200906 对本文的帮助。
一个问题:
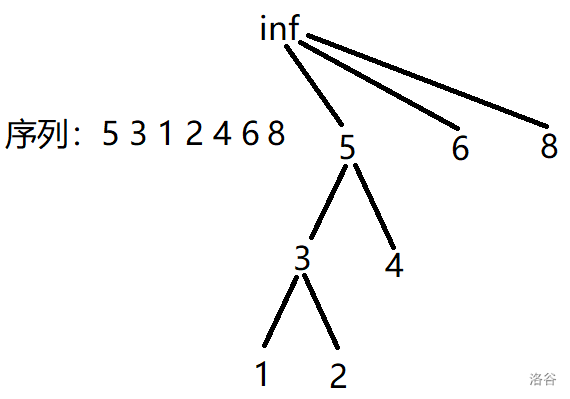
给你一个长为 n 的序列 a。
## 解法:
设区间 $[1,i]$ 形成的单调下降的栈为 $Z_i$。即求 $\max_{i=1}^{n}|Z_i|$ 和 $\sum_{i=1}^{n}|Z_i|$。
对于 $i$,考虑向 $Z_{i,|Z_i|-1}$ 连一条边,最后会连出一片森林。这不方便,不妨考虑在序列的开头插入一个 `inf`,使其变成一棵树,称其为栈树。
考虑修改操作时,就是找到 $x$ 祖先节点中第一个大于 $a_x$ 的节点 $i$,再找到 $i$ 的子节点中第一个大于 $a_x$ 的节点 $j$,将 $dfn$ 序在 $(dfn_i,dfn_j)$ 的子树顺次接到 $x$ 的上,然后再将 $x$ 接到 $i$ 上。
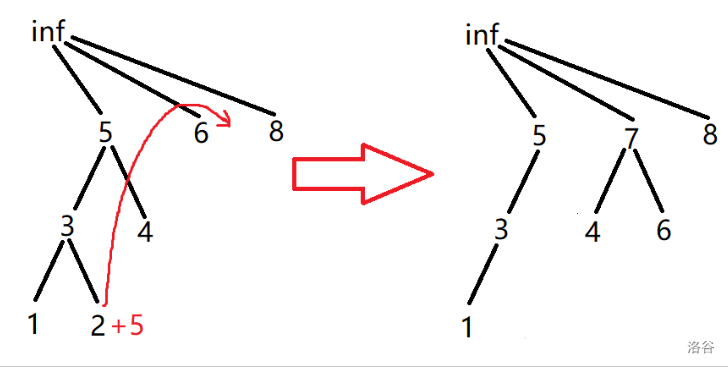
维护考虑括号序,视左括号为 $+1$,右括号为 $-1$,$|Z_i|$ 为位置 $i$ 的前缀和。
这个过程中 $dfn$ 序显然不变,也就是左括号的相对位置不变,那么直接将右括号看成减一的标记,修改操作相当于移动标记,设一次操作需要左移的标记集合为 $S$。
一次移动一个标记显然可以卡到 $O(nq)$,但是我们注意到存在多个右标记在同一个节点的情况,因此考虑先求出 $|S|$,然后每次移动一个点上的所有减一标记,则一次操作的时间复杂度变为 $S$ 中的标记涵盖的点数 $\times\log n$。
### 证明 $q$ 次中 $S$ 中的标记涵盖的点数为 $O(n+q)
考虑 (x,i) 这条链,当一个点右侧存在兄弟节点时,显然需要移动的右括号会存在于一个新的节点,统计这样的点的个数,并将其称为一次操作的代价。
那么考虑 q 次操作后代价总和的上界。将所有右侧存在兄弟节点的点的权值设为 1,其余点为 0,每次操作的代价为 (x,i) 这条链的点权和,将其称为链的代价。
将链的代价分为两部分,一种是初始树中有的,另一种是操作后产生的新代价。
发现每次操作结束后,会将链上的所有节点权值变为 0,且可能产生的新代价 \le2(x 产生的代价,将一个原本为 0 的点改为 1)。
那么一次操作的代价相当于 选出初始树中的代价和新产生的代价的一部分删去,并将新产生的代价总量 +2。
### 关于具体维护
对于标记建线段树,对于每个节点记录信息:左、右端点 $l/r$,最小前缀和 $mn$,前缀和最小的点中最靠右的点的点权 $v$,整段区间的权值总和 $ed$。信息容易合并。
设计以下函数:
`findl(x,val)`:找到最大的 $y$ 满足 $[y,x]$ 的 $v$ 大于 $val$。
`findr(x,val)`:找到最小的 $y$ 满足 $[x,y]$ 的 $v$ 大于 $val$。
`next(x)`:找到最小的 $y$ 满足 $[x,y]$ 的 $mn$ 小于 $0$。
使用 `findl` 即可找到 $i$,进而求出 $|S|$。然后用 `next` 找出下一个需要移动标记的点进行标记移动。最后使用 `findr` 找到 $j$ 就能完成一次修改。
最值和总和在移动时顺便维护即可。
上述三个函数都可以通过线段树二分实现,总时间复杂度 $O((n+q)\log n)$。
## 栈树与笛卡尔树的联系
考虑笛卡尔树的建树,弹栈时将最后一个弹出的点接到当前节点的左儿子。这两个点在栈树上为相邻的兄弟节点。
于是将栈树中所有右侧有兄弟节点的点 断开与其父亲节点的边,向其右侧的兄弟节点连边,就是一颗笛卡尔树。
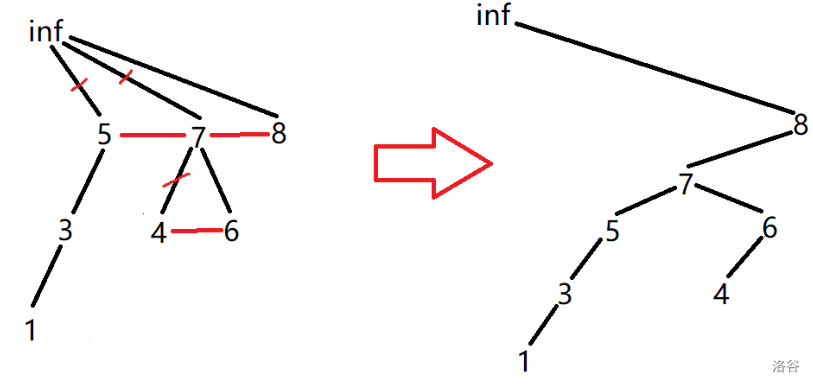
这意味着可以用它维护动态笛卡尔树的形态。前人早已有动态笛卡尔树的相关研究,用的是 `LCT`,但是 `LCT` 难以维护子树最值问题。
于是考虑题目:修改操作不变,要求维护笛卡尔树的一个子树内的最长左、右链的长度。
解法:
容易发现一条右链的长度为它深度最大的节点上 的标记数量减一。
于是可以用 `findl` 和 `findr` 求出一个子树对应在线段树上的的区间 $[l,r]$,答案为区间内节点上 标记数量的最大值减一,注意节点 $r$ 要单独计算。
最长左链的维护只需要从前缀单调栈建树改为后缀单调栈建树即可。
最后以最长右链的维护给出一份代码(值域相同则编号较小的更大):
```cpp
int n,q,a[N];
vector<int>v[N];
int d[N];
int st[N],tp;
struct node{
int mn,ed,v,l,r;//most right v
int mx;
};
struct tree{
node tr[N*4];
node bin(node a,node b){
node k;
b.mn+=a.ed;
k.mn=min(a.mn,b.mn);
k.mx=max(a.mx,b.mx);
k.ed=a.ed+b.ed;
k.v=(a.mn<b.mn?a.v:b.v);
k.l=a.l,k.r=b.r;
return k;
}
void up(int now){
tr[now]=bin(tr[ls],tr[rs]);
}
void build(int now,int l,int r){
if(l==r){
tr[now].ed=1-d[l];
tr[now].v=a[l];
tr[now].l=tr[now].r=r;
tr[now].mx=d[l];
return ;
}
int mid=(l+r)/2;
build(ls,l,mid);
build(rs,mid+1,r);
up(now);
}
void add(int now,int l,int r,int x,int v){
if(l==r){
tr[now].ed-=v;
tr[now].mx+=v;
return ;
}
int mid=(l+r)/2;
if(x<=mid) add(ls,l,mid,x,v);
else add(rs,mid+1,r,x,v);
up(now);
}
void chgv(int now,int l,int r,int x,int v){
if(l==r){
tr[now].v=v;
return ;
}
int mid=(l+r)/2;
if(x<=mid) chgv(ls,l,mid,x,v);
else chgv(rs,mid+1,r,x,v);
up(now);
}
node ask(int now,int l,int r,int x,int y){
if(x<=l&&r<=y) return tr[now];
int mid=(l+r)/2;
if(y<=mid) return ask(ls,l,mid,x,y);
if(x>mid) return ask(rs,mid+1,r,x,y);
return bin(ask(ls,l,mid,x,y),ask(rs,mid+1,r,x,y));
}
node fidl(int now,int l,int r,int x,int v,node rt){
if(l==r) return tr[now];
int mid=(l+r)/2;
if(x<=mid) return fidl(ls,l,mid,x,v,rt);
if(r<=x) {
if(bin(tr[now],rt).v<v) return tr[now];
node k=bin(tr[rs],rt);
if(k.v>=v) return fidl(rs,mid+1,r,x,v,rt);
else return bin(fidl(ls,l,mid,x,v,k),tr[rs]);
}
node k=fidl(rs,mid+1,r,x,v,rt);
if(k.v>=v) return k;
return bin(fidl(ls,l,mid,x,v,k),k);
}
node fidr(int now,int l,int r,int x,int v,node lf){
if(l==r) return tr[now];
int mid=(l+r)/2;
if(x>mid) return fidr(rs,mid+1,r,x,v,lf);
if(x<=l){
if(bin(lf,tr[now]).v<=v) return tr[now];
node k=bin(lf,tr[ls]);
if(k.v>v) return fidr(ls,l,mid,x,v,lf);
else return bin(tr[ls],fidr(rs,mid+1,r,x,v,k));
}
node k=fidr(ls,l,mid,x,v,lf);
if(k.v>v) return k;
return bin(k,fidr(rs,mid+1,r,x,v,k));
}
node nxt(int now,int l,int r,int x,node lf){
if(l==r) return tr[now];
int mid=(l+r)/2;
if(x>mid) return nxt(rs,mid+1,r,x,lf);
if(x<=l){
if(bin(lf,tr[now]).mn>=0) return tr[now];
node k=bin(lf,tr[ls]);
if(k.mn<0) return nxt(ls,l,mid,x,lf);
else return bin(tr[ls],nxt(rs,mid+1,r,x,k));
}
node k=nxt(ls,l,mid,x,lf);
if(k.mn<0) return k;
return bin(k,nxt(rs,mid+1,r,x,k));
}
}t;
int dfn;
void dfs(int now){
dfn++;
for(int t:v[now]) dfs(t);
d[dfn]++;
}
signed main(){
n=read()+1,q=read();
a[1]=inf,st[tp=1]=1;
for(int i=2;i<=n;i++){
a[i]=read();
while(tp>1&&a[st[tp]]<a[i]) tp--;
v[st[tp]].pb(i);
st[++tp]=i;
}
a[n+1]=inf;
dfs(1);
t.build(1,1,n+1);
for(int i=1;i<=q;i++){
int op=read();
if(op==1){//修改
int x=read()+1,v=read();
int s=t.fidl(1,1,n+1,x-1,a[x]+v,{inf,0,0}).ed-1;
t.add(1,1,n+1,x-1,s);
while(s>0){
node k=t.nxt(1,1,n+1,x,{inf,0,0});
k.r--;
if(-k.mn<=s){
t.add(1,1,n+1,k.r,k.mn);
s+=k.mn;
}else{
t.add(1,1,n+1,k.r,-s);
s=0;
}
}
int r=t.fidr(1,1,n+1,x,a[x],{inf,0,0}).r-1;
int nwr=t.fidr(1,1,n+1,x,a[x]+v,{inf,0,0}).r-1;
t.add(1,1,n+1,r,-1);
t.add(1,1,n+1,nwr,1);
a[x]+=v;
t.chgv(1,1,n+1,x,a[x]);
}else{//查询
int x=read()+1;
int l=t.fidl(1,1,n+1,x-1,a[x],{inf,0,0}).l+1;
int r=t.fidr(1,1,n+1,x,a[x],{inf,0,0}).r-1;
if(l==r) pc('0');
else{
node p=t.ask(1,1,n+1,l,r-1);
write(max(p.mx-1,p.ed));
}
pc('\n');
}
}
l_write();
return 0;
}
```