P6617 查找 Search 题解
scp020
·
·
题解
P6617 查找 Search 题解
真的肝死我了,这破题调了好长时间。还是颇有思维量的一道题。
解法
引入
我这道题的思路源自 P5278 那题。那道题可转换为若干子问题,其中之一就是让我们求区间内有无重复数字。
我们可以维护对于每个位置左边第一个与该位置值相同的位置,记作 pre_i。如果不存在该位置,则记为 -1。
显然初始化这个 $pre$ 数组可以做到线性,现在考虑如何维护修改。
我们考虑维护一个集合 $s_i$,其中包含所有值等于 $i$ 的位置。如果将 $a_x$ 的值修改为 $y$,这个操作即为在 $s_{a_x}$ 中删除 $x$,在 $s_y$ 中插入 $x$。这个过程最多只影响 $3$ 个位置的 $pre$,即为 $x$,$x$ 右面第一个等于 $a_x$ 的位置,$x$ 右面第一个等于 $y$ 的位置。过程如图,黑笔为原来的 $pre$ 情况,红笔为修改后的 $pre$ 情况。字有点丑,见笑了。
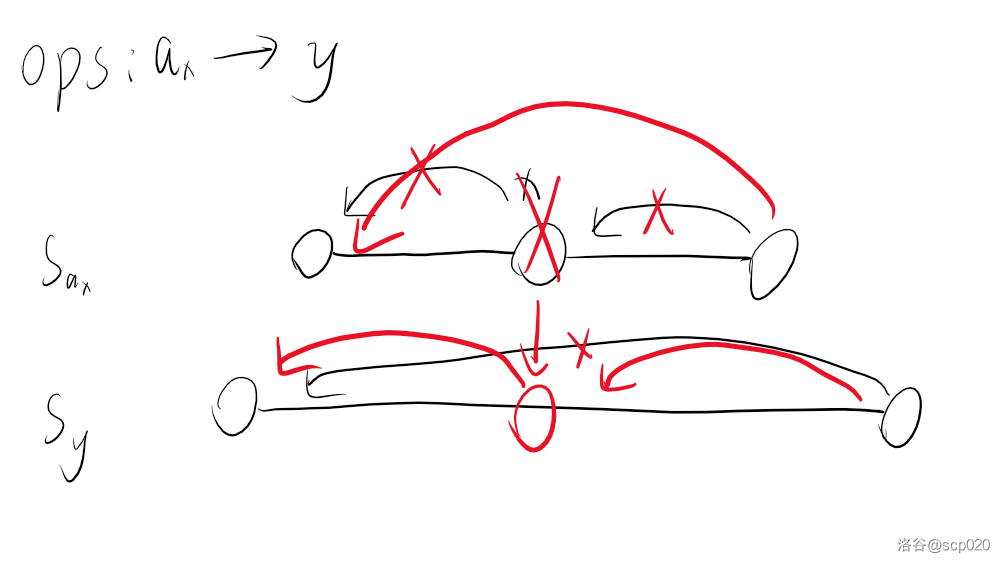
### 迁移
将那道题的思想继承到这道题上。
还是维护数组 $pre$,但是意义有所不同。这里的 $pre$ 维护的是每个位置左边第一个与该位置值相加等于 $w$ 的位置。如果不存在该位置,则记为 $-1$。
需要注意的是,我们这次维护的 $pre$ 需要满足 $\forall i,j \in [1,n],pre_i \neq pre_j$。否则我们的时间复杂度是错的。如图,假若我们将所有的红色点的 $pre$ 都设为绿色点,那么当绿色点的值修改时我们需要修改每个红色点的 $pre$ 值。这么修改时间复杂度可以是 $\mathcal{O}(n)$ 的。
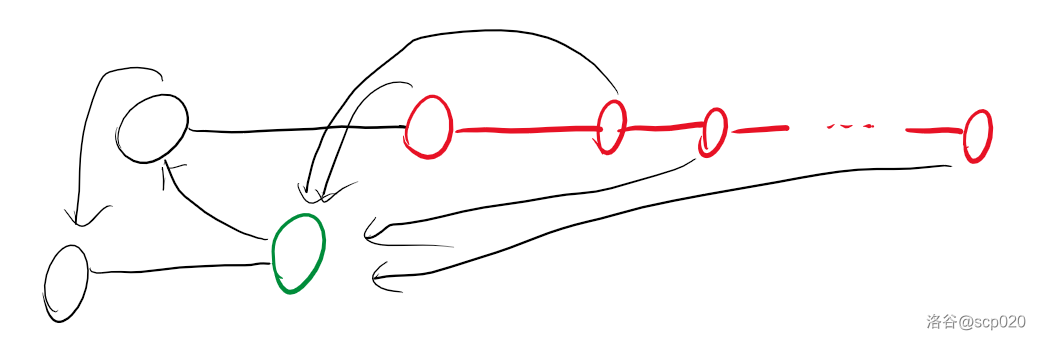
我们可以改进这个问题。因为如果有一个位置 $x \in [l,r]$ 满足 $pre_x \in [l,r]$,那对于 $k \ge x,pre_k = pre_x$,这些 $pre_k$ 都是无效的,不会对答案产生影响。相反,如果有一个位置 $x \in [l,r]$ 不满足 $pre_x \in [l,r]$,那对于 $k \ge x,pre_k = pre_x$,这些 $pre_k$ 也都是无效的,不会对答案产生影响。所以对于每个值,最多只会有一个 $pre$ 值等于它。这些无效的值设为 $-1$ 即可。
我们可以额外维护一个 $ed$ 数组来维护这个值是否已经“被使用”。
这里我们只需要考虑在每次修改中需要更改的位置有哪些。如图,红色点即为可能需要修改的值。最多有 $5$ 个。
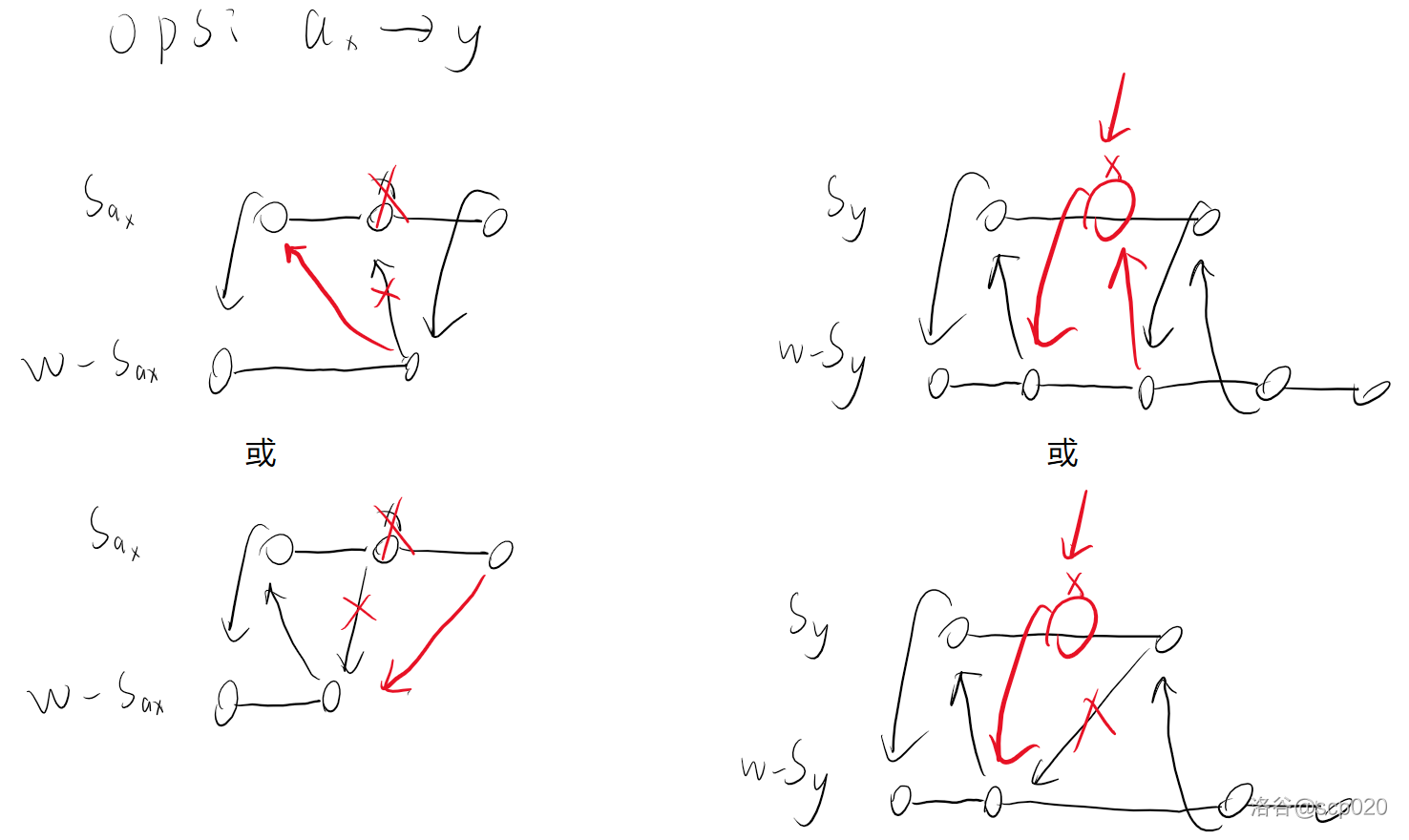
知道了该修改哪些点了,我们就可以比较暴力地修改了。对于每个需要修改的位置 $x$,我们先把 $ed_{pre_x}$ 给解除一下,因为我们后续要进行修改。然后在 $s_{a_x}$ 中查找 $x$ 左边第一个与该位置值相同的位置,进行修改即可。
线段树只是个辅助维护 $pre$ 的工具,在本题中不是重点,不过多介绍了。线段树维护区间 $pre$ 最大值。
## 代码
```cpp
#include<bits/stdc++.h>
namespace fast_IO
{
#define Getchar() p1==p2 and (p2=(p1=Inf)+fread(Inf,1,1<<21,stdin),p1==p2)?EOF:*p1++
#define Putchar(c) p3==p4 and (fwrite(Ouf,1,1<<21,stdout),p3=Ouf),*p3++=c
char Inf[1<<21],Ouf[1<<21],*p1,*p2,*p3=Ouf,*p4=Ouf+(1<<21);
inline void read(int &x,char c=Getchar())
{
bool f=c!=45;
x=0;
while(c<48 or c>57) c=Getchar(),f&=c!=45;
while(c>=48 and c<=57) x=(x<<3)+(x<<1)+(c^48),c=Getchar();
x=f?x:-x;
}
inline void write(int x)
{
if(x<0) Putchar(45),x=-x;
if(x>=10) write(x/10),x%=10;
Putchar(x^48);
}
inline void write(std::string st)
{
for(int i=0;i<st.size();i++) Putchar(st[i]);
}
};
using namespace fast_IO;
int n,m,w,a[500010],pre[500010],ed[500010];
std::unordered_map< int,std::set<int> > mp;
struct node
{
int mpre;
node *lc,*rc;
inline void pushup()
{
mpre=std::max(lc->mpre,rc->mpre);
}
};
class seg_tree
{
#define ls l,mid
#define rs mid+1,r
private:
node *root;
inline node *build(int l,int r)
{
node *rt=new node;
if(l==r) rt->mpre=pre[l];
else
{
int mid=(l+r)/2;
rt->lc=build(ls),rt->rc=build(rs),rt->pushup();
}
return rt;
}
inline void fix(node *rt,const int &pos,const int &val,int l,int r)
{
if(l==r)
{
rt->mpre=val;
return;
}
int mid=(l+r)/2;
if(pos<=mid) fix(rt->lc,pos,val,ls);
else fix(rt->rc,pos,val,rs);
rt->pushup();
}
inline int ask(node *rt,const int &L,const int &R,int l,int r)
{
if(L<=l && r<=R) return rt->mpre;
int mid=(l+r)/2,ret=0;
if(L<=mid) ret=std::max(ret,ask(rt->lc,L,R,ls));
if(R>mid) ret=std::max(ret,ask(rt->rc,L,R,rs));
return ret;
}
public:
inline void build()
{
root=build(1,n);
}
inline void fix(const int &pos,const int &val)
{
fix(root,pos,val,1,n);
}
inline int ask(const int &L,const int &R)
{
return ask(root,L,R,1,n);
}
};
seg_tree tree;
std::vector< std::pair<int,int> > v;
inline void addget(const int &val,const int &it)
{
if(pre[it]!=-1) ed[pre[it]]=0;
v.push_back(std::make_pair(val,it));
}
inline void getpre(const int &val,const int &it)
{
if(mp[w-val].empty())
{
pre[it]=-1,tree.fix(it,pre[it]);
return;
}
std::set<int>::iterator it2=mp[w-val].lower_bound(it);
if(it2==mp[w-val].begin()) pre[it]=-1,tree.fix(it,pre[it]);
else
{
it2--;
if(ed[*it2])
{
if(ed[*it2]>=it) pre[ed[*it2]]=-1,tree.fix(ed[*it2],pre[ed[*it2]]),ed[*it2]=it,pre[it]=*it2,tree.fix(it,pre[it]);
else pre[it]=-1,tree.fix(it,pre[it]);
}else ed[*it2]=it,pre[it]=*it2,tree.fix(it,pre[it]);
}
}
inline void deladd()
{
for(int i=0;i<v.size();i++) getpre(v[i].first,v[i].second);
v.clear();
}
int main()
{
// freopen("example.in","r",stdin);
// freopen("example.out","w",stdout);
read(n),read(m),read(w);
for(int i=1;i<=n;i++) read(a[i]);
std::set<int>::iterator it1,it2,it3;
for(int i=1,prev;i<=n;i++)
{
if(!mp[w-a[i]].size()) pre[i]=-1;
else
{
prev=*(--mp[w-a[i]].end());
if(ed[prev]) pre[i]=-1;
else pre[i]=prev,ed[prev]=i;
}
mp[a[i]].insert(i);
}
tree.build();
for(int i=1,op,l,r,ans=0;i<=m;i++)
{
read(op),read(l),read(r);
if(op==1)
{
it1=mp[a[l]].find(l),it2=mp[w-a[l]].lower_bound(l);
if(it2!=mp[w-a[l]].end()) addget(w-a[l],*it2);
if(it1!=mp[a[l]].end())
{
it1++;
if(it1!=mp[a[l]].end()) addget(a[l],*it1);
}
if(pre[l]!=-1) ed[pre[l]]=0;
mp[a[l]].erase(l),mp[r].insert(l),a[l]=r;
it1=mp[a[l]].find(l),it2=mp[w-a[l]].lower_bound(l),addget(a[l],*it1);
if(it2!=mp[w-a[l]].end()) addget(w-a[l],*it2);
if(it1!=mp[a[l]].end())
{
it1++;
if(it1!=mp[a[l]].end()) addget(a[l],*it1);
}
deladd();
}else
{
l^=ans,r^=ans;
if(tree.ask(l,r)>=l) write("Yes\n"),ans++;
else write("No\n");
}
}
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}
```