题解[P9501 likely]

· · 题解

原题链接

题意：求满足 \sum\limits_{k=0}^{n-1}\prod\limits_{j=0}^{m-1}a_{(k+j)\bmod n}=k,\forall_{i\in[0,n)}\ a_{i}=\pm 1 的 a 的数量。

为方便考虑，以下下标均自动对 n 取模，\oplus 指异或，\bigoplus 指异或和。

重新设 A_{i}\!=\!0/1，并将限制条件改为 \sum\limits_{k=0}^{n-1}(-1)^{\bigoplus \limits_{0\leq j<m}A_{k+j}}=k。

首先考虑 m=1 怎么做，此时 \sum\limits_{k=0}^{n-1}(-1)^{A_i}=k，设 A_i=1 的 i 的个数为 p，则有 -p+n-p=k，所以 p=\frac{n-k}{2}（n-k 不是偶数时答案必为 0）。那这时答案显然为 \binom{n}{p}。

对于一般情况，设 B_i=\bigoplus \limits_{0\leq j<m}A_{i+j}，则 B_i 中 1 的个数有 p=\frac{n-k}{2} 个，即 \sum\limits_{0\leq i<n}B_i=p。

考虑统计 B 的个数，而 B 由 A 确定，那接下来要重点做的是便是：

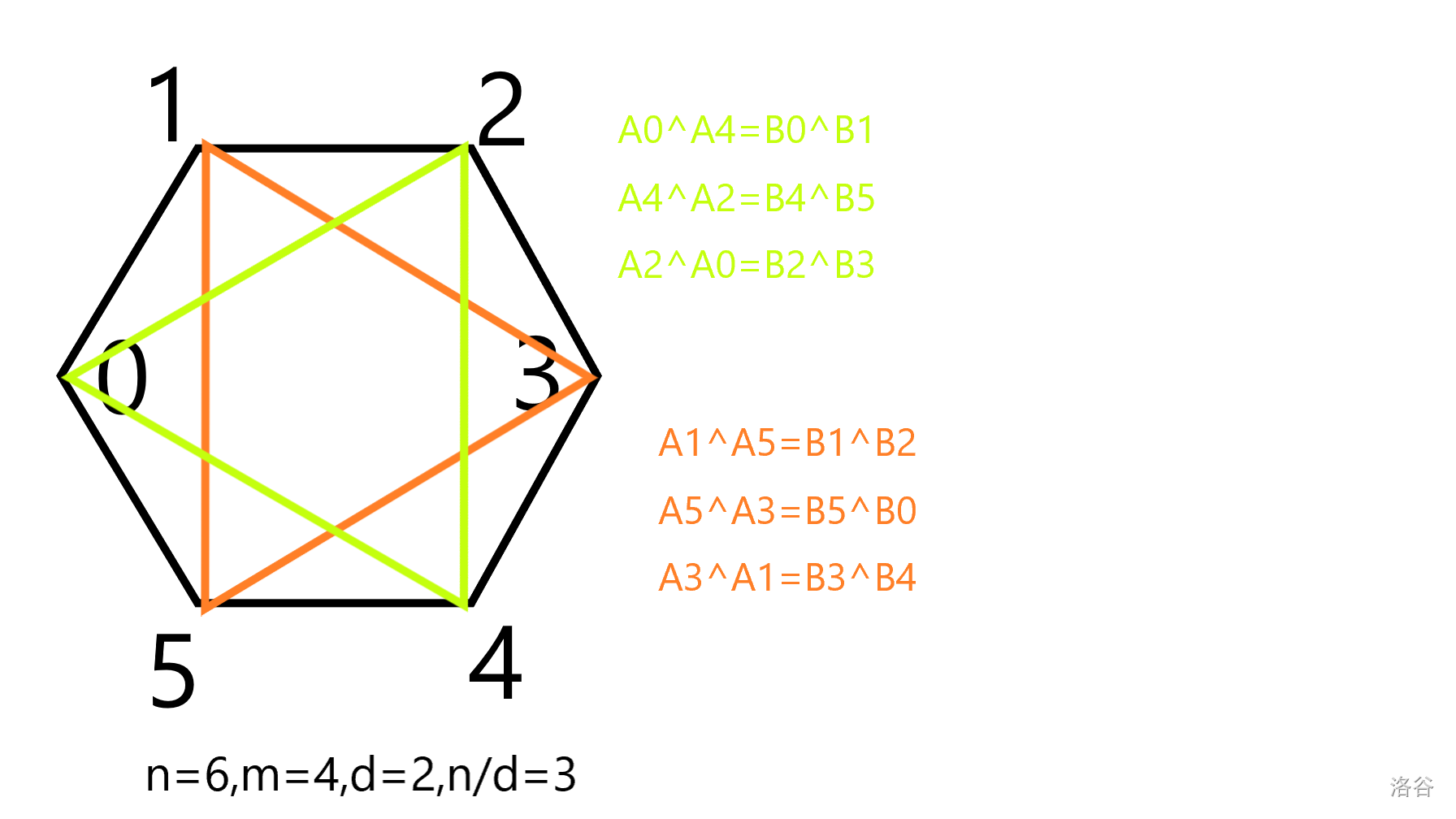
$2.$ 找到关系 $B_i=\bigoplus \limits_{0\leq j<m}A_{i+j}$ 中蕴含的 $B$ 的限制条件。 ### $\text{Step 1}:$ $A$ 与 $B$ 的对应关系 假设我们已经有了一个序列 $B$，考虑如何生成所有满足条件的 $A$。 由于 $A_i\oplus A_{i+m}=B_i \oplus B_{i+1}$，等号右边是确定的，所以当 $A_i$ 确定时直接可以推出 $A_{i+m},A_{i+2m}\cdots$。他们间的关系组成了一个长度为 $\frac{n}{\gcd(n,m)}$ 的环，而一共有个 $\gcd(n,m)$ 个环。 ![](https://cdn.luogu.com.cn/upload/image_hosting/gtri6nh1.png) 设 $d=\gcd(n,m)$，则我们只需确定 $A_0,A_1\cdots A_{d-1}$ 就能得出全部数。 而 $B_i=\bigoplus \limits_{0\leq j<m}A_{i+j}$ 等价于 $A_i\oplus A_{i+m}=B_i \oplus B_{i+1}$ 并且 $B_0=\bigoplus \limits_{i=0}^{m-1}A_i$。接下来着重看第二个等式。 由于相差 $d$ 的倍数的下标之间的关系已经明确，**所以 $B_{0}=\bigoplus \limits_{0\leq j<m}A_{j}$ 本质上是 $B_0$ 等于 $m/d$ 个 $A_0\oplus A_1\oplus \cdots \oplus A_{d-1}$ 相异或，再异或上一个已知的数**。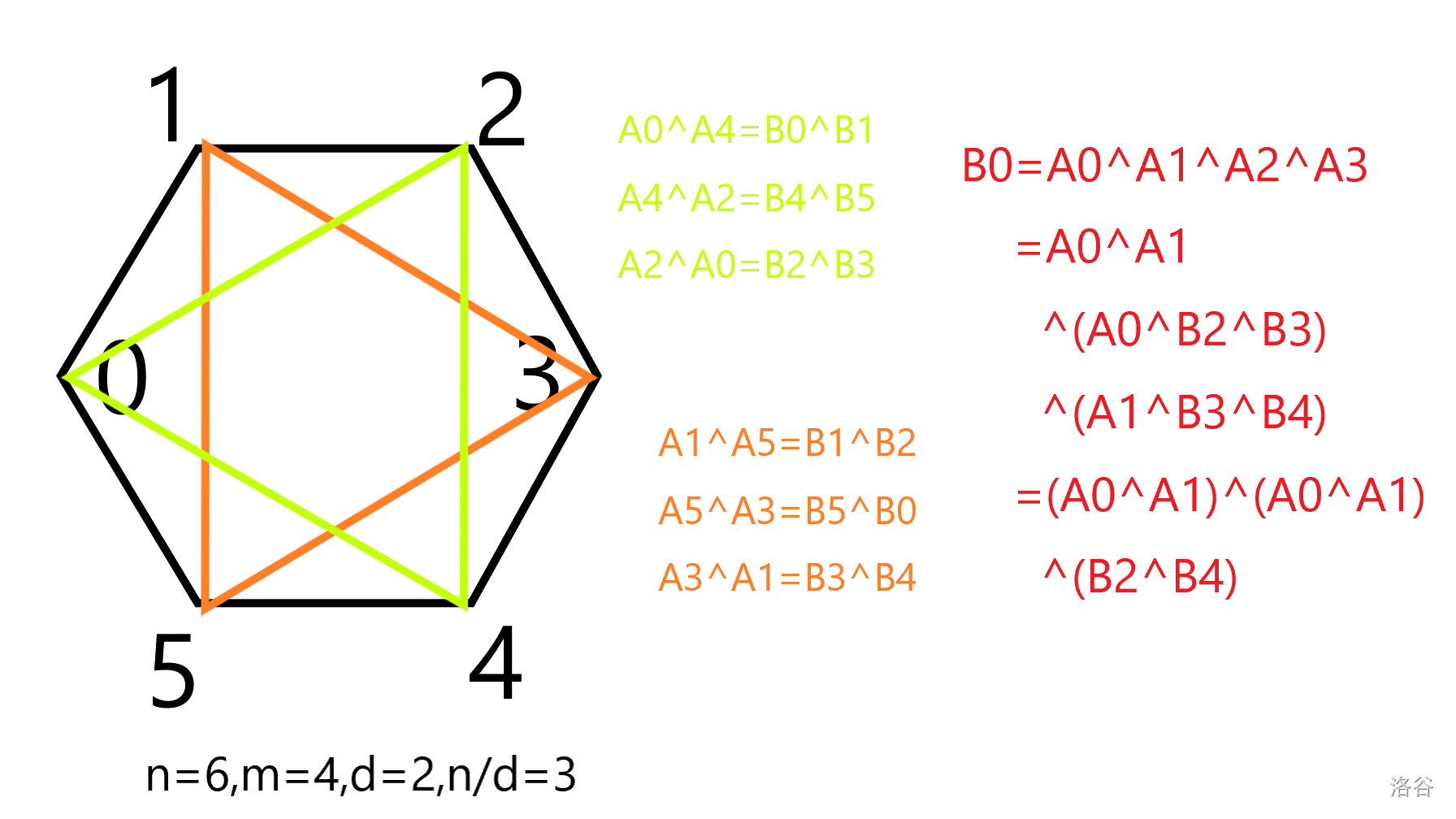 ![](https://cdn.luogu.com.cn/upload/image_hosting/r0qov496.png) 当 $m/d$ 是偶数时，$A_0,A_1\cdots A_{d-1}$ 分别出现偶数次，都自己跟自己异或没了，不再有对他们间的限制，方案数为 $2^d$。 当 $m/d$ 是奇数时，$A_0\oplus A_1\oplus \cdots \oplus A_{d-1}$ 会将明确等于一个数 $0/1$。由于在所有情况下，所有数异或起来等于 $0$ 和等于 $1$ 的方案数相同（改变一个数则一一对应），方案数为 $2^{d-1}$。 所以每个 $B$ 会对应 $2^{d-[m/d\in \mathrm{odd}]}$ 个 $A$。 ### $\text{Step 2}:$ $B$ 的限制条件 对于一个环，相邻两个 $A$ 间的限制条件是 $A_i\oplus A_{i+m}=B_i \oplus B_{i+1}$。但由于这是一个环，将所有这样的关系异或起来后，等号左边的 $A$ 会变成 $0$（每个数出现两次），所以 $B_{i}\oplus B_{i+1}\oplus B_{i+m}\oplus B_{i+1+m}\oplus \cdots=0$。 设 $C_i=\bigoplus \limits_{j=0}^{n/d-1}B_{i+jd}$，即一个环上所有 $B$ 的异或和，上面说的就是对所有 $i$ 都有 $ C_{i}\oplus C_{i+1}=0$，所以 $C_i=C_{i+1}$。于是所有的 $C_i$ 要么全部等于 $0$，要么全部等于 $1$。也就是说每个环上 $B$ 的和**要么全是奇数，要么全是偶数**。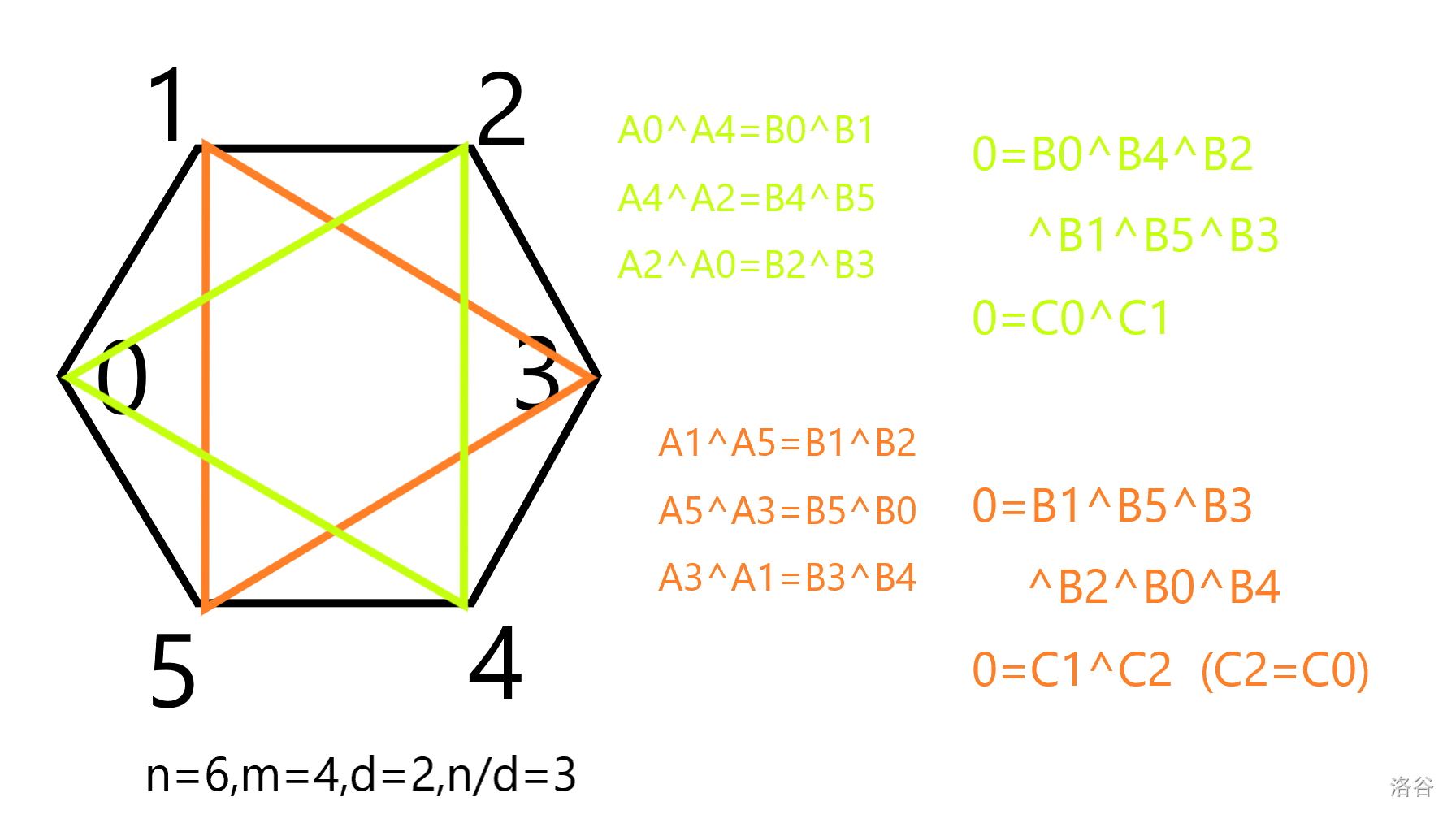 ![](https://cdn.luogu.com.cn/upload/image_hosting/kpdlg0a3.png) 还不止这一限制，依然重新考虑 $B_{0}=\bigoplus \limits_{i=0}^{d-1}A_i$。 根据之前的讨论，当 $m/d$ 是偶数时，$A$ 全消掉了，事实上我们能推导出 $C_{i}$ 必定是 $0$（$\text{Step 1}$ 的第二张图红字等价于 $B_0\oplus B_{2}\oplus B_{4}=0$）。($m/d$ 是奇数时肯定不会有限制，因为和 $A$ 有关。) 证明如下： 由于 $m/d$ 是偶数，$d|m/2$，所以对任意的 $i$，$i$ 和 $i+m/2$ 在同一个环内。 为构建 $A_{i}$ 与 $A_{i+m/2}$ 间的关系，设 $S_i$ 代表从 $i$ 开始，每次将下标 $+m$ 并对 $n$ 取模，直到下标为 $i+m/2$，此过程中遍历到的下标上（包括 $i$ 而**不**包括 $i+m/2$）所有 $B$ 的异或和，那么就有 $A_i\oplus A_{i+m/2}=S_{i}\oplus S_{i+1}$（不断由 $A_{i}\oplus A_{i+m}=B_{i}\oplus B_{i+1}$ 异或得来）。 所以 $B_{0}=\bigoplus \limits_{0\leq i<m/2}A_i\oplus A_{i+m/2}=\bigoplus \limits_{0\leq i<m/2}S_{i}\oplus S_{i+1}=S_{0}\oplus S_{m/2}$。 考虑一下 $S_{0}\oplus S_{m/2}$ 是什么，求 $S_0$ 过程中遍历的最后一个下标 $+m$ 就是 $m/2$，而 $S_{m/2}$ 又以 $0$ 结尾（$0\!+\!m\!=\!\frac{m}{2}\!+\!\frac{m}{2}$），所以这就是从 $0$ 开始，不断将下标 $+m$，直到回到 $0$ 的所有下表标上对应 $B$ 的异或和，注意 $0$ 出现了两次，那这就是 $C_{0}\oplus B_{0}$。 所以 $B_{0}=C_{0}\oplus B_{0}$，也就是 $C_{0}=0$，于是 $C_{0,1\cdots d-1}=0$。 ### $\text{Summary}

设 t=n/d，即一个环的长度。

当 m/d 是偶数时，每个环上都只能有偶数个 B 是 1，B 一共要有 p 个 1，每个 B 对应 2^d 个 A，所以答案是：

2^d[x^p]\left(\sum_{2|i}\binom{t}{i}x^i\right)^d=[x^p]\left((1+x)^{t}+(1-x)^{t}\right)^d

当 m/d 是奇数时，每个环上 B 的和的奇偶性相同，每个 B 对应 2^{d-1} 个 A，答案是：

2^{d-1}[x^p]\left(\sum_{2|i}\binom{t}{i}x^i\right)^d+\left(\sum_{2|i+1}\binom{t}{i}x^i\right)^d=[x^p]\dfrac{\left((1+x)^{t}+(1-x)^{t}\right)^d+\left((1+x)^{t}-(1-x)^{t}\right)^d}{2}

直接 \text{Ln}+\text{Exp} 求多项式 d 次幂，O(n\log n) 巨大常数显然过不了。

把他们俩展开，分别有 \begin{cases}\displaystyle \sum_{i}\binom{d}{i}\sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k,m/d\in \mathrm{even}\\\displaystyle \sum_{2|i}\binom{d}{i}\sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k,m/d\in \mathrm{odd}\end{cases}，于是有了 O(pd) 的做法，也不太行。

（这部分解法是参考了题解区的）但由于已经有了封闭形式，多项式的次数不超过 n，按着 \text{FFT} 的方法，将 n 补成 2 的幂 N 后，对于点值 \omega_{N}^k 可以直接快速幂算，单次复杂度 O(\log t+\log d=\log n)，而需要的只有一项的系数，可以将点值直接乘上 \text{IDFT} 时的贡献系数得到。

一个小优化：998244353=1+7\times 17\times 2^{23}，所以不一定 N 硬要是 2 的幂，还可以是 7 或者 17,119 乘上 2 的某次幂。

这样复杂度是 O(n\log n) 的，代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e6+10;
const int mod=998244353;
int n,m,p,a,b,ans,nn;
int fac[N],ifac[N];
#define sub(x,y) x<y?x-y+mod:x-y
inline int qpow(int x,int k){
    int res=1;
    while(k){
        if(k&1)res=1ll*res*x%mod;
        x=1ll*x*x%mod;k>>=1; 
    }
    return res;
}
void work(){
    int N1=1;while(N1<=n)N1<<=1;
    int N2=7;while(N2<=n)N2<<=1;
    int N3=17;while(N3<=n)N3<<=1;
    int N4=119;while(N4<=n)N4<<=1;
    int N=min({N1,N2,N3,N4});
    p=N-p;
    int i,w=qpow(3,(mod-1)/N),wp=qpow(w,p),v=1,vp=1,x,y;
    if((m/b)&1){
        for(i=0;i<N;++i,v=1ll*v*w%mod,vp=1ll*vp*wp%mod){
            x=qpow(1+v,a);y=qpow(mod+1-v,a);
            ans=(1ll*(qpow(x+y,b)+qpow(sub(x,y),b))*vp+ans)%mod;
        }
        ans=1ll*ans*qpow(N,mod-2)%mod;
        ans=ans&1?ans+mod>>1:ans>>1;
    }
    else {
        for(i=0;i<N;++i,v=1ll*v*w%mod,vp=1ll*vp*wp%mod){
            x=qpow(1+v,a);y=qpow(mod+1-v,a);
            ans=(1ll*qpow(x+y,b)*vp+ans)%mod;
        }
        ans=1ll*ans*qpow(N,mod-2)%mod;
    }
}
void main_(){
    cin>>n>>m>>p;ans=0;
    if((n-p)&1)return puts("0"),void();
    p=(n-p)>>1;
    b=__gcd(n,m);a=n/b;
    work();
    cout<<ans<<'\n';
}
int main(){
    int T;cin>>T;
    while(T--)main_();
}

还没结束，这题实际上能 O(n)，且不依赖于 \text{NTT} 模数。

回到答案的展开式，后面的求和都是 \displaystyle \sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k，其中 i\leq d，所以 ti\leq n。

于是只需求出所有的 f_i=\displaystyle \sum_{k}\binom{i}{k}\binom{n-i}{p-k}(-1)^k,0\leq i\leq n。

这很像范德蒙德卷积，却偏偏多了一个 (-1)^k，像 \mathcal{Concrete Mathematics},\mathcal{A=B} 等著作也没见着他的影。

但他还是能递推的，可以手搓 \text{Zeilberger's Algorithm} 得到答案：

f_{i+1}=\dfrac{1}{n-i}\left(V f_{i}-Uf_{i-1}i\right) U=\dfrac{2+3n+n^2-3p-2np+p^2}{(n-p)^2+3(n-p)+2} V=\dfrac{2n+3n^2+n^3-4p-9np-4n^2p+6p^2+5mp^2-2p^3}{(n-p)^2+3(n-p)+2}

我真的不信这玩意能有组合意义。

推导过程过于复杂，由于篇幅限制就不再展开，有兴趣的看这里。

由于 x^2+3x+2\equiv 0\pmod {mod} 的解集只能是 \{mod-1,mod-2\}，n-p 完全没有那么大，所以不用担心分母为 0。

代码没必要放了吧，就一个递推式的事。

\text{} \text{} \text{} \text{}

最优解到底是怎么回事呢？