题解:P10145 [WC2024] 线段树
Petit_Souris
·
·
题解
感觉难度还行,也不是不可做题...不过之前被同学剧透过一小部分了,所以考场上我估计也不会做。不过这题基本上大部分还是自己做出来的,赢。
首先很显然的一步:对于一个线段树的区间 [l,r),在 l,r 之间连一条无向边。那么一个区间 [L,R) 的和能被表示出来当且仅当在图上 L,R 连通。
我们观察一下这个图建出来长成什么样:
先考虑一下特殊性质怎么做。可以设 f_u 表示 u 子树中符合条件,L_u 和 R_u 连通的方案数;g_u 表示 u 子树中符合条件,L_u 和 R_u 不连通的方案数。
转移:
$g_u=f_{ls}g_{rs}+g_{ls}f_{rs}$(一边连通一边不连通,$l\to r$ 必须不连)
这样可以获得 20 分。
接下来考虑一下一般情况怎么做,我们发现这个图(是一个平面图)有非常好的性质:当 $L,R$ 不连通时,对于区间 $[L,mid)$,如果其中一个点和 $R$ 连通,那么 $[mid,R)$ 中所有点不可能和 $l$ 连通。
画个图就明白为什么了:
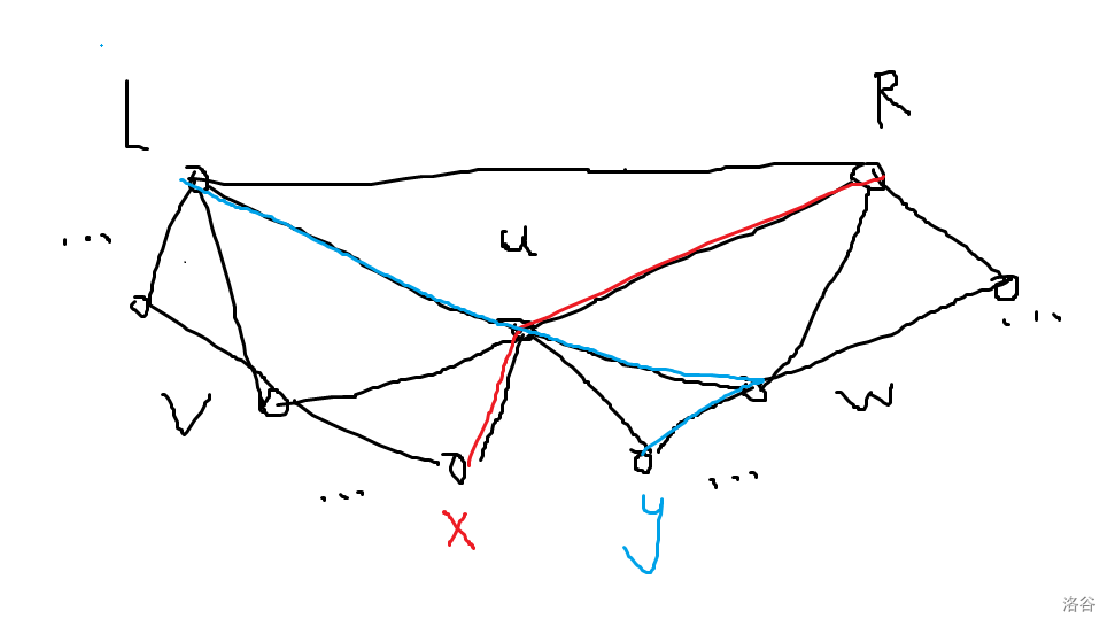
两条路径会在 $mid$ 处相交。
因此考虑这样设计 dp 状态:设 $f_u$ 为子树 $u$ 中,$L_u,R_u$ 是连通的方案数,$g_{u,i}$ 表示子树 $u$ 中,所有 $\le i$ 的点与 $L_u$ 连通,其余点与 $R_u$ 连通的方案数。
转移的时候,和上面的分类类似,还有一种转移是 $g_{ls,i}$ 和 $g_{rs,j}$ 合并,这时候需要满足 $[i+1,j]$ 中的点和外面的点之间不能有限制。这个限制可以用 xor - hash 处理,对于每个限制 $[qL,qR]$,在 $qL,qR$ 处异或上同样一个权值。如果两个点 $i,j$ 的异或前缀和相同,那么可以进行转移。这样可以做到多项式复杂度,获得 40 左右的分数。
这样状态和 $i$ 关系就不大了,重点实际上在权值,所以可以离散化一下并记录权值,现在合并转移就变成了 $g_{ls,i}\times g_{rs,i}\to g_{u,i}$。其他转移也可以一一列出,在此不表。
暴力可以做到 $\mathcal O(nm)$,结合特殊性质得到 85 分。发现形式非常优美,都是在 $i$ 相同的下标进行操作,所以立刻条件反射出线段树合并。合并的时候,如果一侧子树空了就直接打乘法 tag,一路递归到叶子节点直接算一下新的 $g$ 就行了。
时间复杂度和空间复杂度都是 $\mathcal O(n\log n)$,实现起来不难,比 NOI2020 命运写起来简单多了,但是比那个题难想多了。
```cpp
#include<bits/stdc++.h>
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
#define pii pair<ll,ll>
#define rep(i,a,b) for(ll i=(a);i<=(b);++i)
#define per(i,a,b) for(ll i=(a);i>=(b);--i)
using namespace std;
bool Mbe;
ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void write(ll x){
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
}
const ll N=5e5+9,O=2e7+9,Mod=998244353;
mt19937_64 rnd(time(0));
ll n,m,k,Ls[N],Rs[N],Mid[N],ql[N],qr[N];
ull w[N],tw[N];
ll f[N],tot,tr[O],tag[O];
int ls[O],rs[O],totn,rt[N];
ll Build(ll l,ll r){
ll x=++tot;
if(l+1==r)return x;
ll mid=read();
Mid[x]=mid;
Ls[x]=Build(l,mid);
Rs[x]=Build(mid,r);
return x;
}
void Pushtag(int x,ll k){
tr[x]=tr[x]*k%Mod;
tag[x]=tag[x]*k%Mod;
}
void Pushdown(int x){
if(tag[x]==1)return ;
if(ls[x])Pushtag(ls[x],tag[x]);
if(rs[x])Pushtag(rs[x],tag[x]);
tag[x]=1;
}
void Upd(int&x,ll l,ll r,ll u,ll v){
if(!x)x=++totn,tag[x]=1,tr[x]=ls[x]=rs[x]=0;
if(l==r)return tr[x]=v,void();
ll mid=(l+r)>>1;
Pushdown(x);
if(u<=mid)Upd(ls[x],l,mid,u,v);
else Upd(rs[x],mid+1,r,u,v);
tr[x]=(tr[ls[x]]+tr[rs[x]])%Mod;
}
int Merge(int x,int y,ll l,ll r,ll wx,ll wy){
if(!x){
Pushtag(y,wy);
return y;
}
if(!y){
Pushtag(x,wx);
return x;
}
if(l==r){
tr[x]=(tr[x]*wx+tr[y]*wy+tr[x]*tr[y])%Mod;
return x;
}
Pushdown(x),Pushdown(y);
ll mid=(l+r)>>1;
ls[x]=Merge(ls[x],ls[y],l,mid,wx,wy);
rs[x]=Merge(rs[x],rs[y],mid+1,r,wx,wy);
tr[x]=(tr[ls[x]]+tr[rs[x]])%Mod;
return x;
}
ll Query(ll x,ll l,ll r,ll u){
if(!x||l==r)return tr[x];
ll mid=(l+r)>>1;
Pushdown(x);
if(u<=mid)return Query(ls[x],l,mid,u);
return Query(rs[x],mid+1,r,u);
}
void dfs(ll x,ll l,ll r){
if(l+1==r){
f[x]=1,Upd(rt[x],1,k,w[l],1);
return ;
}
dfs(Ls[x],l,Mid[x]);
dfs(Rs[x],Mid[x],r);
f[x]=2*f[Ls[x]]*f[Rs[x]]%Mod;
rt[x]=Merge(rt[Ls[x]],rt[Rs[x]],1,k,f[Rs[x]],f[Ls[x]]);
f[x]=(f[x]+tr[rt[x]])%Mod;
}
bool Med;
int main(){
cerr<<fabs(&Med-&Mbe)/1048576.0<<"MB\n";
n=read(),m=read();
Build(0,n);
rep(i,1,m){
ql[i]=read(),qr[i]=read();
ull W=rnd();
w[ql[i]]^=W,w[qr[i]]^=W;
}
tw[0]=w[0];
rep(i,1,n)w[i]^=w[i-1],tw[i]=w[i];
sort(tw,tw+n+1);
k=unique(tw,tw+n+1)-tw;
rep(i,0,n)w[i]=lower_bound(tw,tw+k,w[i])-tw+1;
dfs(1,0,n);
write((f[1]+Query(rt[1],1,k,1))%Mod);
cerr<<"\n"<<clock()*1.0/CLOCKS_PER_SEC*1000<<"ms\n";
return 0;
}
```