『FCRT / 1 - 4』Century
ChatSheep
·
·
题解
题解
如果您并没有数位动态规划的基础,可以看看出题人写的烂笔记。
Subtask 1
### Subtask 3
这里是一个数位动态规划模板,本质就是问你 $0\sim C_1$ 中,有多少个数字,满足任意的 $j$ 都满足第 $j$ 位小于等于 $R_j$。
这个只需要记录一个标记表示是否小于 $C_1$ 即可,从高到低位做,转移是显然的。
### Subtask 4
这一步大概可以理解为 $m$ 个数位动态规划同时进行,所以直接先记录 $m$ 个标记,实际写代码的时候可以考虑状态压缩,用一个二进制数表示列标记的状态。
那么假定我们进行到了第 $i$ 行,就直接枚举当前这一行的数字是什么(而不是一个数位),直接检查是否满足这 $m$ 个标记的限制,并且直接转移即可。
时间复杂度是 $O(n 10^m 2^m)$,感觉比正解复杂,不推荐写。
### Subtask 5
数位动态规划的本质就是用来优化枚举的数字的,既然内层又套了一层枚举,就继续用数位动态规划优化。
具体来说,流程是从上到下、从左往右的顺序填写每一个格子,结合轮廓线的思想,只维护当前这个格子所对应轮廓线上的标记状压值即可。
具体来说,整个算法的运行状况大约如图下所示(蓝色和绿色的就是轮廓线):
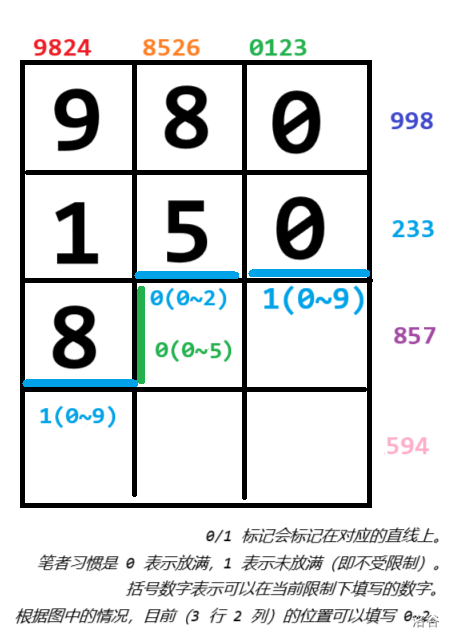
比如目前的格子,如果填写 $2$,那么当前这一行(绿色)的标记会改变为 $1$。而列(蓝色)的标记,如果仍然填写 $2$,那么标记不变。
转移后,第二列的蓝色轮廓线将会下降一格,备用于下一列的处理,绿色轮廓线将会右移一格,与正常的动态规划无异。
这一档很宽松,能保证不管常数有多大都能得到这一部分分。
### Subtask 6, 7, 8
仔细分析 Subtask 5 的复杂度,发现是 $O(nm 2^m)$ 的。似乎能能得到 $100$ 分,但是实际上内部仍然是由一个枚举 $0\sim9$ 的数位的过程。带上两倍常数运算量大约为 $1.69\times10^{9}$,几乎过不了。
不过内部枚举 $0\sim9$ 的数位其实只有两种本质不同的数位,一种是会让至少一种标记不会更新,一种是都不会让标记更新的。
第一种显然只会有一个数,也就是目前标记状态的情况下可以填写的最大数位,转移不需要任何代价。
第二种显然就是所有小于这个最大数位的数位,这些数位的转移都是一样的,因为不管怎样比较都是小于,直接加上新转移的状态值与方案数的乘积即可。
这样就省去了 $10$ 倍的常数,由于空间不足以开 $18\times18\times2^{18}$ 的数组,所以使用滚动数组优化。
## 代码(正常写法)
```cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 18;
int n, m, dp[2][N][1 << N][2], r[N][N], c[N][N];
inline int stat(int i, int j, int lim, int llim) { // 获取正确的状态值,书写代码方便。
if (i == n - 1 && j == m) return 1;
if (j == m) return dp[(i + 1) & 1][0][lim][0];
return dp[i & 1][j][lim][llim];
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for (int i = 0; i < n; ++i) {
long long x; cin >> x;
for (int j = m - 1; j >= 0; --j) {
r[i][j] = x % 10;
x /= 10;
}
}
for (int i = 0; i < m; ++i) {
long long x; cin >> x;
for (int j = n - 1; j >= 0; --j) {
c[i][j] = x % 10;
x /= 10;
}
}
for (int i = n - 1; i >= 0; --i) {
for (int j = m - 1; j >= 0; --j) {
for (int lim = 0; lim < (1 << m); ++lim) {
for (int llim = 0; llim <= 1; ++llim) {
long long ans = 0;
int d1 = (llim ? 9 : r[i][j]);
int d2 = ((1 << j) & lim) ? 9 : c[j][i];
int mind = min(d1, d2); // 计算出最大可以填的数位
ans += stat(i, j + 1, (lim | (mind != c[j][i] ? (1 << j) : 0)), llim | (mind != r[i][j]));
if (mind) ans += 1ll * mind * stat(i, j + 1, lim | (1 << j), 1); // 剩下的就是固定的转移,只要乘方案数即可
dp[i & 1][j][lim][llim] = ans % 998244353;
}
}
}
}
cout << dp[0][0][0][0] << "\n";
return 0;
}
```
## 挑战最优解(标程写法)
1. 直接定义 $(i,n)$ 的下一个格子是 $(i+1,1)$,于是又可以滚动掉无用的一维,这样不仅可以省下一个长度 $18$ 的状态,还减少了时间常数。
2. 可以用定期取模。通过估算发现 $9^9 \times 998244353$ 很接近了 $64$ 位整数的范围,所以只需要在转移 $9$ 次后统一取模即可。
3. 循环的最后一层是枚举的是当前行的标记,这个循环直接展开即可。
4. 在第三步基础上去除一些冗余代码。以及其他的卡常。
这样写跑得飞起,轻轻松松卡近 $\text{250ms}$,虽然第二条卡常很抽象,但即使不用也能跑到大约 $\text{430ms}$。
```cpp
#include <iostream>
#include <algorithm>
#define int long long
using namespace std;
const int N = 18, p = 998244353;
int n, m, dp[2][1 << N][2];
int r[N*N], c[N*N];
signed main() {
cin >> n >> m;
for (int i = 0; i < n; ++i) {
long long x; cin >> x;
for (int j = m - 1; j >= 0; --j) {
r[i * m + j] = x % 10;
x /= 10;
}
}
for (int j = 0; j < m; ++j) {
long long x; cin >> x;
for (int i = n - 1; i >= 0; --i) {
c[i * m + j] = x % 10;
x /= 10;
}
}
for (int lim = 0; lim < (1 << m); ++lim) {
for (int llim = 0; llim <= 1; ++llim) {
dp[(n * m) & 1][lim][llim] = 1;
}
}
for (int id = n * m - 1; id >= 0; --id) { // 优化 1,需要注意判断列边界。
for (int lim = 0; lim < (1 << m) ; ++lim) {
// 循环展开,优化 3
int mind = std::min((int)r[id], ((lim >> (id % m)) & 1) ? 9 : c[id]);
dp[id & 1][lim][0] =
(dp[(id + 1) & 1][lim | (mind != c[id] ? (1 << (id % m)) : 0)][(id % m == m - 1 ? 0 : (mind != r[id]))] +
1ll * mind * dp[(id + 1) & 1][lim | (1 << (id % m))][(id % m == m - 1 ? 0 : 1)]);
mind = ((lim >> (id % m)) & 1) ? 9 : c[id];
dp[id & 1][lim][1] =
(dp[(id + 1) & 1][lim | (mind != c[id] ? (1 << (id % m)) : 0)][id % m != m - 1] +
1ll * mind * dp[(id + 1) & 1][lim | (1 << (id % m))][(id % m == m - 1 ? 0 : 1)]);
}
if (id % 9 == 0) { // 优化 2
for (int lim = 0; lim < (1 << m); ++lim) {
dp[id & 1][lim][0] %= p;
dp[id & 1][lim][1] %= p;
}
}
}
cout << dp[0][0][0] % p; // 记得最后取模
return 0;
}
```
## 闲话
如果您有什么特别厉害的正确做法比标程还要快很多,欢迎与出题人交流。
另外由于新的线路开通,为了修建 $\color{#f2a900}\dfrac{0}{6}\color{black}/\color{e4002b}\dfrac{1}{14}\color{black}/\color{862041}\dfrac{9}{4}\color{black}/\color{#665ec4}\dfrac{27}{9}$ 站的四线换乘我不知道需要多少世纪。