考虑将式子反过来:对于所有的 a\in[2,p-1],若 a^{p-1}\equiv\pmod{p},则 p 为素数。
这就是费马素性测试。
但是这个定理不是真名题,存在特殊情况,即对于所有 a\perp n,都有 a^{n-1}\pmod{n},但 n 是合数,这种数叫 Carmichael 数。
如何解决这些数呢?
Miller-Rabin 素性测试
这是基于一个叫二次探测定理的方法,具体内容是:
如果 p 是奇素数,对于 x^2\equiv1\pmod{p} 方程的解为 x\equiv1\pmod{p} 或 x\equiv p-1\pmod{p}
这个定理只能判奇素数,不过偶素数也只有 2 罢了。(误)
于是乎,对于 a^{n-1}\equiv 1\pmod{n},我们设 u\times2^t=n-1,那么便可以令 v=a^u\bmod n,然后根据二次探测定理依次平方然后判断,最多平方 t 次。
然后注意到如果 $a$ 是随机选的话可能会 `rp--`(虽然概率确实很小),所以我们可以选前 12 个质数来当 $a$,这样在值域小于 $2^{78}$ 时都能过掉,当然我不会证明。(
code here:(马蜂难看致歉)
```cpp
int pr[] = {114514, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
bool mlrb(int x) {
if (x <= 37 || x % 2 == 0) { // 特判
for (int i = 1; i <= 12; i++) if (x == pr[i]) return 1;
return 0;
}
int r = x - 1, t = 0;
while (r % 2 == 0) r /= 2, t++;
for (int i = 1; i <= 12; i++) {
if (pr[i] > x) break;
int v = qp(pr[i], r, x);
if (v == 1 || v == x - 1) continue;
for (int j = 1; j <= t; j++) {
v = (__int128)v * v % x; // long long 会乘爆
if (v == x - 1) break;
if (j == t) return 0;
}
}
return 1;
}
```
# Pollard Rho 算法
~~东坡肉算法~~
Pollard Rho 算法可以在 $O(n^{1/4})$ 复杂度内求出 $n$ 的一个非平凡因子。
考虑如果这个非平凡因子 $p$ 满足 $p\mid k$,那么 $\gcd(k, n) > 1$。
怎么寻找这个 $k$ 呢,考虑构造一个 $f(x)=x^2+c\pmod{n}$,然后再构造一个 $k_n=f(k_{n-1})$,这里的 $c$ 和 $k_1$ 都是随机得到。
于是我们随机一下看看($n=8137, c=17, k_1=719$):
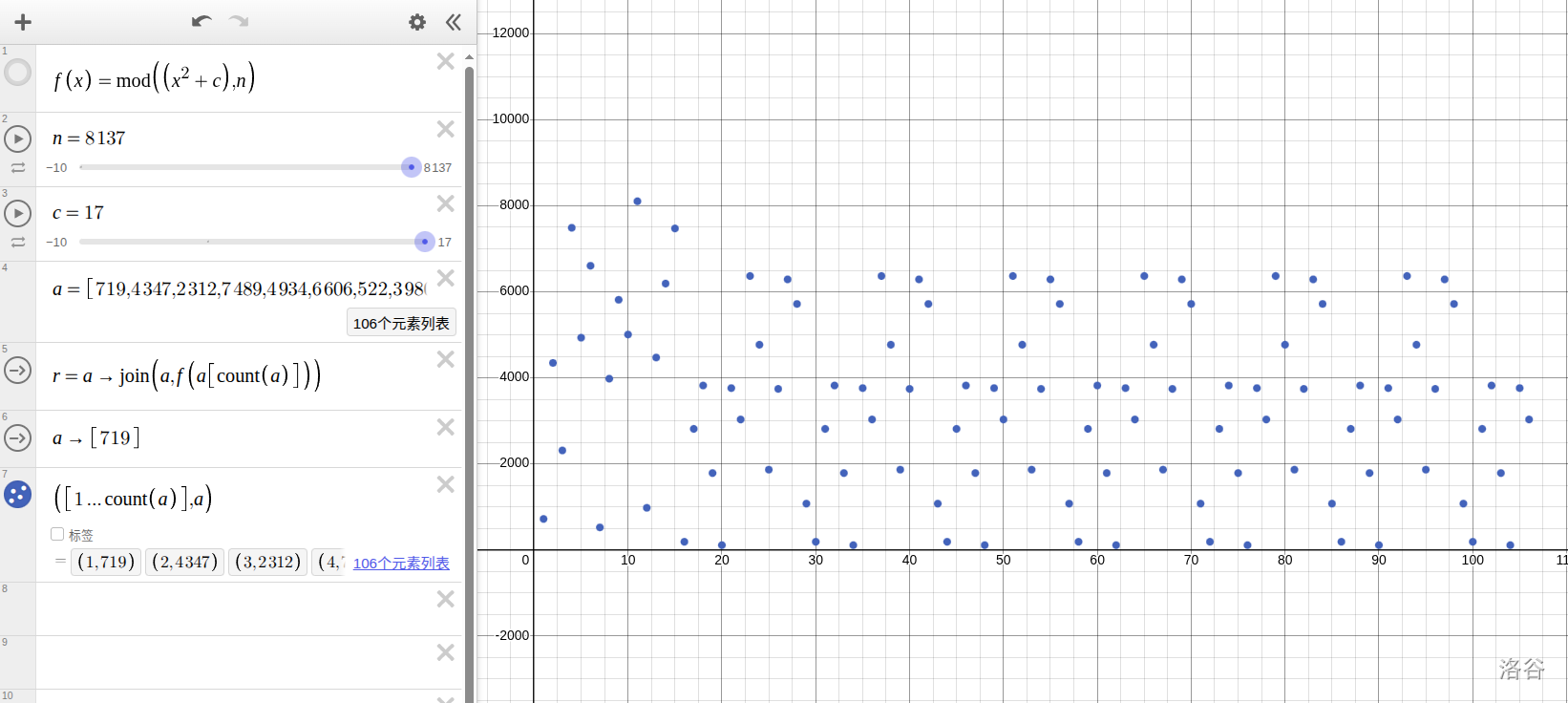
~~(desmos 你是我的神)~~
可以明显发现有循环部分,这也是 `rho` 的由来。
再注意到若 $x\equiv y\pmod{n}$,则 $f(x)\equiv f(y)\pmod{n}$。这保证了我们转移是没有问题的。
于是我们使用一个 floyd 判环,用两个数 $x, y$ 一个跳一步一个条两步,如果 $x = y$,说明我们已经进入环中,就完蛋了,否则对于 $\gcd(|x-y|, n) > 1$, 就有非平方因子 $p = \gcd(|x-y|, n)$。(终于用到第 2 段的结论了 qwq)
是的会爆,可恶可恨可悲的数据。
我们还有优化!将每次要求的 $2^{lim}$ 个 $|x-y|$ 都乘起来,最后再统一计算 $\gcd$,同时我们有结论最多累乘 127 次可过,就可以跑得飞快。
code:
```cpp
int f(int x, int c, int p) { return ((__int128)x * x % p + c) % p; }
int plr(int n) {
if (n == 4) return 2;
int c = rnd(1, n - 1), x = rnd(0, n - 1), y = x;
x = f(x, c, n), y = f(f(y, c, n), c, n);
for (int lim = 1; x != y; lim <<= 1) {
int cnt = 1;
for (int i = 1; i <= lim; i++) {
int tmp = (__int128)cnt * abs(x - y) % n;
if (!tmp) break;
cnt = tmp;
x = f(x, c, n), y = f(f(y, c, n), c, n);
}
int d = gcd(cnt, n);
if (d != 1) return d;
}
return n;
}
```
## 最大质因子
我们可以使用 dfs,对于每个 $p \neq n$,如果使用 Miller-Rabin 判断后是质数就记录答案,否则就递归下去,同时还要递归 $\frac{n}{p}$。
code:
```cpp
int ans;
void dfs(int n) {
if (n == 1) return;
if (mlrb(n)) {
ans = max(ans, n);
return;
}
int d = plr(n);
while (d == n) d = plr(n);
dfs(d);
dfs(n / d);
}
```
---
于是这道题就做完了,放上完整代码:
```cpp
#include <bits/stdc++.h>
#define eps 1e-12
#define inf LONG_LONG_MAX
#define int long long
#define endl '\n'
using namespace std;
const int maxn = 1e5 + 10, mod = 1e9 + 7;
mt19937_64 rng(time(0));
int qp(int a, int b, int p = mod) {
int res = 1;
a %= p;
while (b) {
if (b & 1) res = (__int128)res * a % p;
a = (__int128)a * a % p, b >>= 1;
}
return res;
}
int pr[] = {114514, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
bool mlrb(int x) {
if (x <= 37 || x % 2 == 0) {
for (int i = 1; i <= 12; i++) if (x == pr[i]) return 1;
return 0;
}
int r = x - 1, t = 0;
while (r % 2 == 0) r /= 2, t++;
for (int i = 1; i <= 12; i++) {
if (pr[i] > x) break;
int v = qp(pr[i], r, x);
if (v == 1 || v == x - 1) continue;
for (int j = 1; j <= t; j++) {
v = (__int128)v * v % x;
if (v == x - 1) break;
if (j == t) return 0;
}
}
return 1;
}
int rnd(int l, int r) { return rng() % (r - l + 1) + l; }
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
int f(int x, int c, int p) { return ((__int128)x * x % p + c) % p; }
int plr(int n) {
if (n == 4) return 2;
int c = rnd(1, n - 1), x = rnd(0, n - 1), y = x;
x = f(x, c, n), y = f(f(y, c, n), c, n);
for (int lim = 1; x != y; lim <<= 1) {
int cnt = 1;
for (int i = 1; i <= lim; i++) {
int tmp = (__int128)cnt * abs(x - y) % n;
if (!tmp) break;
cnt = tmp;
x = f(x, c, n), y = f(f(y, c, n), c, n);
}
int d = gcd(cnt, n);
if (d != 1) return d;
}
return n;
}
int ans;
void dfs(int n) {
if (n == 1) return;
if (mlrb(n)) {
ans = max(ans, n);
return;
}
int d = plr(n);
while (d == n) d = plr(n);
dfs(d);
dfs(n / d);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--) {
int x;
cin >> x;
if (mlrb(x)) cout << "Prime" << endl;
else {
ans = 0;
dfs(x);
cout << ans << endl;
}
}
return 0;
}
```
$THE\quad END