题解 P3024 【[USACO11OPEN]Cow Checkers S】
Water_Cows
·
·
题解
吐槽一句,题解里面写的都是啥啊。。。威佐夫博弈对于我们这些蒟蒻来说,太难了。
$\texttt{UPDATE 2021.3.6}$ 修改一些细节。
### Part 1 找规律
在模拟赛上看到这种题,第一眼看到的就应该想到找规律。
我们首先把胜负的图画出来。注:红色表示 Farmer John 胜,蓝色表示 Bessie 胜。
[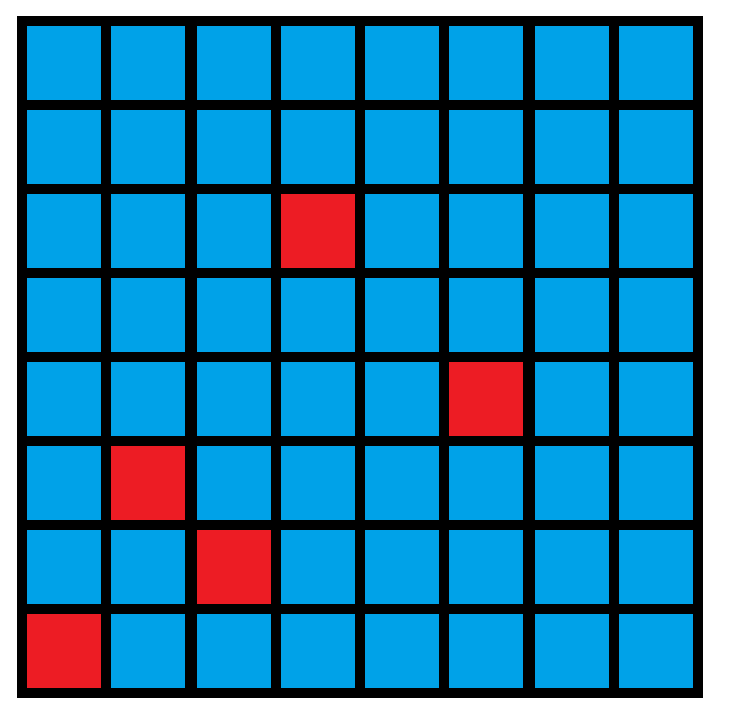](https://imgchr.com/i/yDckoq)
感觉太少了,没关系,再来!
[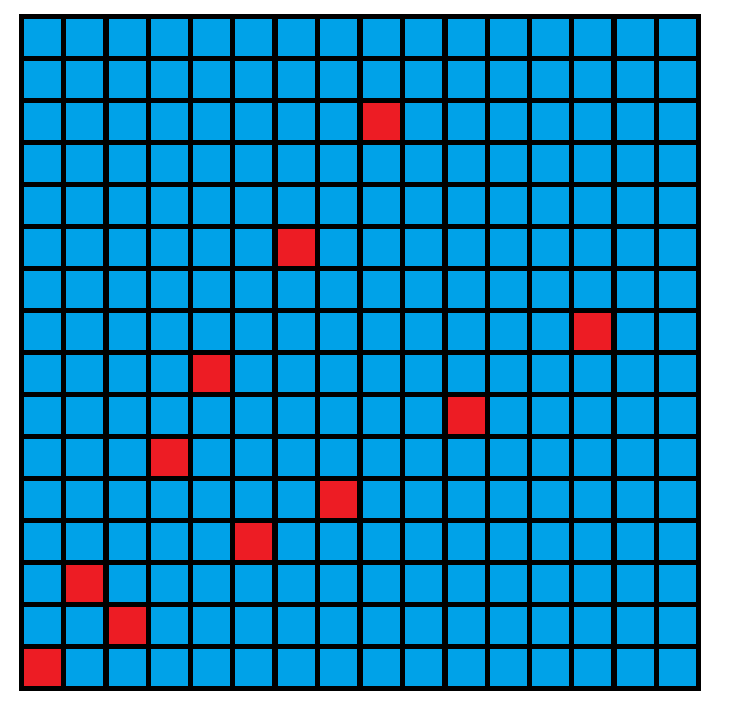](https://imgchr.com/i/yDcZWT)
~~感觉我的手要断了。~~
有兴趣的读者可以继续画下去,~~反正我是不画了~~。
我们把每个点的坐标写出来:
$$(0, 0), (1, 2), (2, 1), (3, 5), (4, 7), (5, 3), (6, 10), (7, 4), (8, 13), (10, 6), (13, 8)$$
我们发现,哦不,没有发现,这~~毛~~玩样有什么(~~毛个~~)规律啊?
但是有一点我们可以发现,就是红色的东西是关于 $y=x$ 这条直线对称的(说给初一及以下的同学听,就是关于正方形对角线对称的)。
好,那我们重新写一遍出来:
$$(0, 0), (1, 2), (3, 5), (4, 7), (6, 10), (8, 13)$$
还是没什么规律啊?把一个点横纵坐标做个差看看?
$$0, 1, 2, 3, 4, 5$$
!!!发现了吧,**等差数列**!!!
### Part 2 得出规律
所以可以得出规律:从 $1$ 至 $n$(横坐标的值)每次加上 $k$($k$ 每次加 $1$),得到的值,为纵坐标的值,这个坐标则 Bessie 一定输的点。
### Part 3 发现一个 Bug
还有一个问题:怎么确定横坐标的值,毕竟横坐标并不是从 $1$ 到 $n$ 按顺序的。
考虑在同一行内,至多会有一个红格子 $B$。原因:
- 当这个格子 $A$ 在红格子 $B$ 左边时,一定可以找到从这个格子一步走到另一个红格子 $C$ 的方法,那么 Bessie 从先手变成了后手,而红格子意味着后者会赢,所以这个格子 $A$ 是先手赢。
- 当这个格子 $A$ 在红格子 $B$ 的右边时,一定可以先向左走走到红格子 $B$,那么 Bessie 从先手变成了后手,而红格子意味着后者会赢,所以这个格子 $A$ 是先手赢。
既然我们发现的这个规律,由于 $N$ 和 $M$ 在 $1$ ~ $1000000$ 之间,可以开一个一维数组,下标表示横坐标的值,数组值记录的值为对应的纵坐标的值。之后就执行以下操作:
- 当 $f_i$ 还没有对应纵坐标的值的时候,根据规律计算出 $f_i$ 的值,同时把 $f_{f_i}=i$。因为两个点是关于 $y=x$ 对称的。
- 当 $f_i$ 有对应纵坐标的值的时候,直接跳过,因为这一行已经有红色的点了。
然后就可以 $\mathcal{O(1)}$ 查询了。每次有一个起始坐标 $(x, y)$,则判断 $x$ 对应的纵坐标是否为 $y$,如果是,则 Bessie 输,否则则赢。
### Part 4 代码
```cpp
#include <iostream>
using namespace std;
const int N = 1e6 + 7;
int f[(N<<1)+1], t;
// 记得数组开两倍
// 后面 +1 就是一个习惯,毕竟数组的大小开奇数好像会快一点
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
// 平时写题可以用用,可以增加 cin 和 cout 速度,但是不能用 scanf 和 printf 了
// 千万注意考试别用,RE 抱蛋两行泪
for(int k=0, i=1; i<=(int)1e6; i++)
if(!f[i]) f[i] = i + (++k), f[f[i]] = i;
cin >> t >> t >> t;
// 读 3 个 t 就是因为 n 和 m 没用,节省变量,反正会覆盖的
for(int i=1; i<=t; i++) {
int x, y;
cin >> x >> y;
if(f[x] == y) cout << "Farmer John\n";
else cout << "Bessie\n";
}
}
```
泥们是不是要~~感谢~~一下我这个良心题解,没有泥们看不懂的东西,要公式去别的题解看就好了,~~求赞~~。