题解:P1525 [NOIP2010 提高组] 关押罪犯 || 拓展域并查集
_Weslie_
·
·
题解
这篇文章主要介绍拓展域并查集。
拓展域并查集,主要用于一种状态表示无法解决问题的题目。例如本题,一个开关有两种状态,用和不用。
本文主要介绍二倍拓展域的拓展域并查集。
什么是拓展域并查集?
拓展域并查集是一种数据结构,用于解决具有多个相互关系集合的问题。它是传统并查集的扩展,能够处理集合间的不同关系,如相互排斥或相互独立的关系。
拓展域并查集有什么用?
只看定义是不可以的,我们来看一个应用场景:
这个问题我们直接用普通并查集是无法通过的,我们必须换一个更加高级的办法。
在原本的并查集中,$i$ 号点在并查集中对应的点正好为 $i$,而在拓展域并查集中对应的是 $i$ 和 $i+n$ 等。当然这个题只需要 $i$ 和 $i+n$ 就够了,有些需要 $i+2n$ 之类的。
例如:对于以下样例,如果我们使用普通并查集,建出来的图是这样的:
```
4 6
1 2
2 3
3 4
4 5
5 6
6 1
```
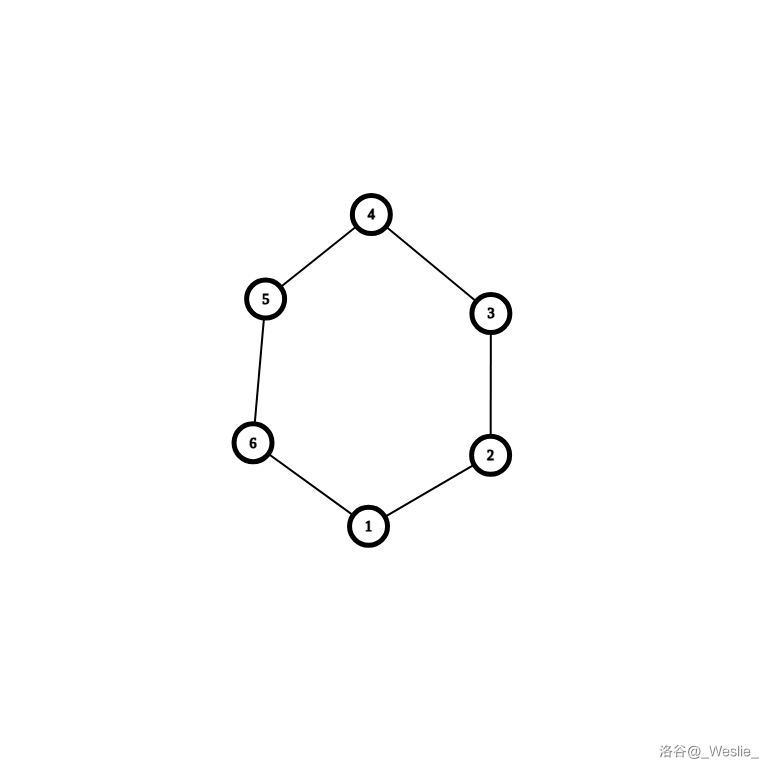
但是如果我们对于下面的样例,结果是这样的:
```
4 7
1 2
2 3
3 4
4 5
5 6
6 7
7 1
```
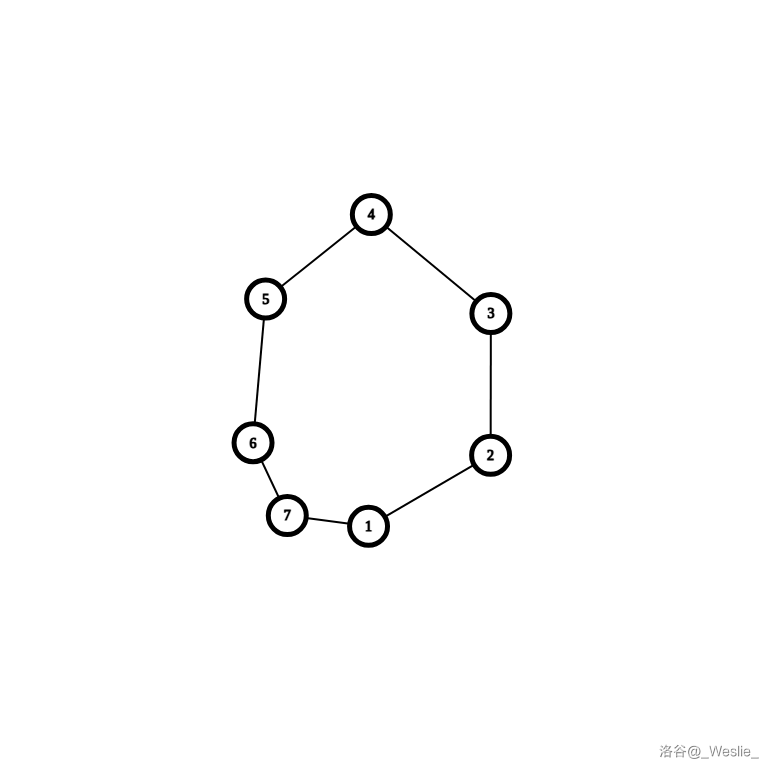
这张图除了比上面这张多了一个点之外,与上面一张基本没有什么区别,如果我们仅仅只使用并查集的话,是看不出什么区别的。
所以这个使用普通并查集是不可取的。
我们使用拓展域并查集,$u$ 和 $u+n$ 分别表示点 $u$ 的两个相反状态,将 $(u,v+n)$ 连边表示 $(u,v)$ 不应该在一个集合里(也可以看做 $u$ 和 $v$ 的反状态在一个集合里)。当然 $(u,v+n)$ 存在边了,相反地,$(v,u+n)$ 也理应右边。
那么就好办了,判断不可以的方式是存在 $u$ 的正反状态在一个集合里。
附上上面两个样例的图:
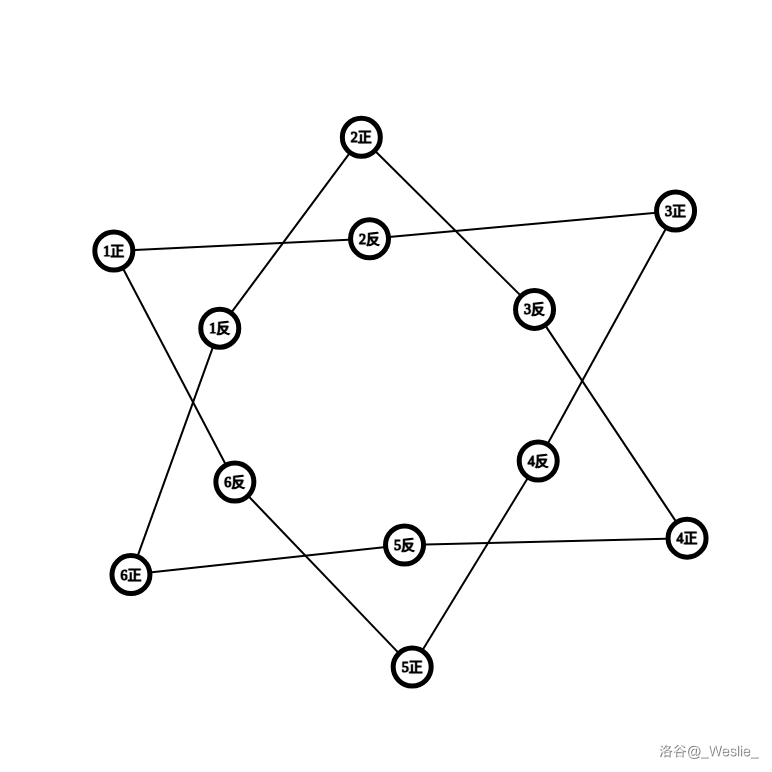
等效图:
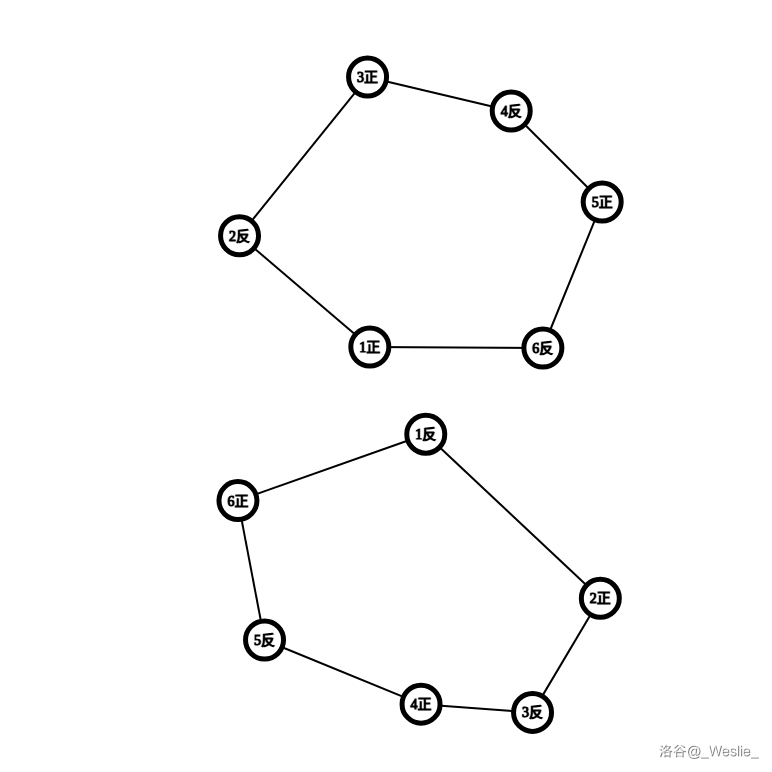
可以看到这张图明显没有任何 $u$ 的正反状态在一个集合里。
但是第二组的样例就不一样了。
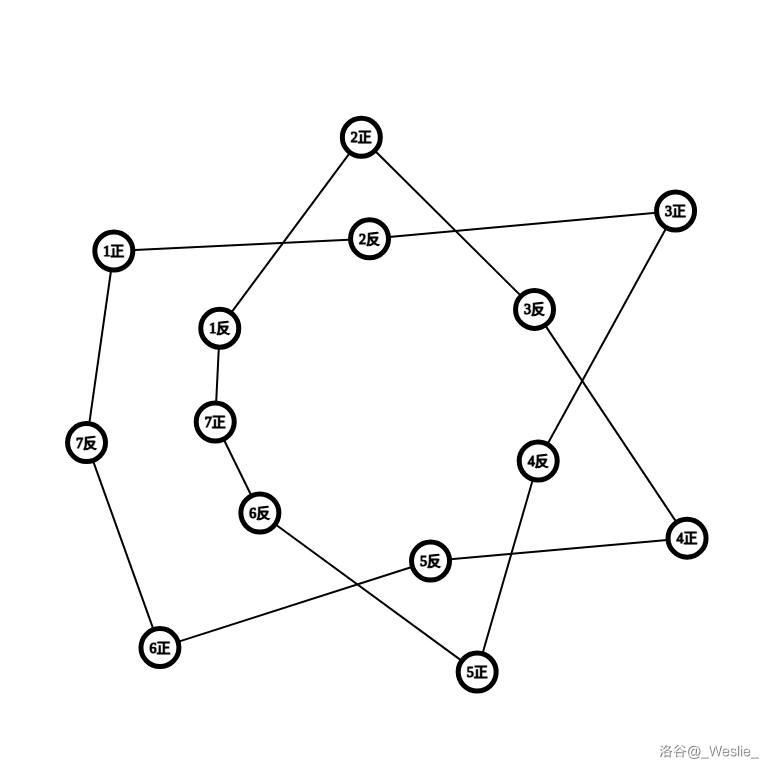
不够直观?看看这张等效图:
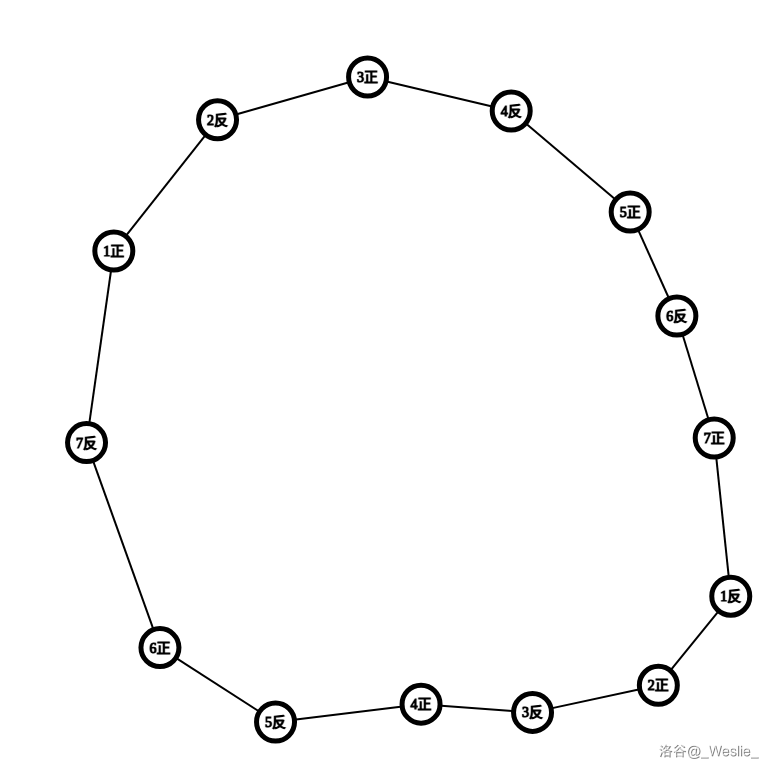
可以看出点 $1$ 的正反两个状态在一个集合里,所以不行。
## 拓展域并查集怎么写?
拓展域并查集在写法上仅有初始化与两点连边与普通并查集不同。
初始化:
```
for(int i=1;i<=2*n;i++)fa[i]=i;//2 倍点
```
查询父亲和合并函数与普通并查集一样。
```
int findd(int now){
if(fa[now]==now)return now;
return fa[now]=findd(fa[now]);
}
void vnion(int u,int v){
u=findd(u);v=findd(v);
if(u==v)return;
fa[u]=v;
}
```
连边:
```
int u,v;
vnion(u,v+n);
vnion(v,u+n);
```
如果需要集合大小,集合内包含的元素等,直接与普通并查集相同写即可。
## 例题
### P1525 [NOIP2010 提高组] 关押罪犯
[题目传送门。](https://www.luogu.com.cn/problem/P1525)
我们贪心,对影响力从大到小排序。
每遇到一个事件,因为如果让这两个囚犯 $(u,v)$ 在一个监狱内,答案就是这个事件的影响力了。我们尽量尝试让最大影响力发生在后面的时间上,所以我们将 $u$ 与 $v$ 的反状态关在一个监狱里。
当你发现 $u$ 与 $u$ 的反状态关在一个监狱里时,这说明已经没救了,无论如何你都避免不了打架,那么就输出当前影响力即可(显然你可以操控使得影响力最小的事件在一个监狱内发生)。
```
#include<bits/stdc++.h>
using namespace std;
struct node{
int u,v,w;
}e[100005];
bool cmp(node _,node __){
return _.w>__.w;
}
int fa[40005];
int findd(int now){
if(fa[now]==now)return now;
return fa[now]=findd(fa[now]);
}
void vnion(int u,int v){
u=findd(u),v=findd(v);
if(u==v)return;
fa[u]=v;
}
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=2*n;i++)fa[i]=i;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
}
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++){
vnion(e[i].u+n,e[i].v);
vnion(e[i].u,e[i].v+n);
if(findd(e[i].u)==findd(e[i].u+n)||findd(e[i].v)==findd(e[i].v+n)){
printf("%d",e[i].w);
return 0;
}
}
printf("0");
return 0;
}
```
### CF776D The Door Problem
[题目传送门。](https://www.luogu.com.cn/problem/CF776D)
这题最难的是状态设计。也因此这题是蓝。
每个钥匙都有动或不动两种状态,分别设为 $i$ 和 $i+m$。
那么我们对于每个门,看看它初始开不开。设控制它的两把钥匙为 $(u,v)$:
- 如果门初始开,$(u,v)$ 只能同时选或不选,合并 $(u,v)$ 及 $(u+m,v+m)$。
- 如果门初始关,$(u,v)$ 只能二选其一,合并 $(u+m,v)$ 及 $(u,v+m)$。
```
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
vector<int>g[N];
int fa[N],n,a[N],m;
int findd(int now){
if(fa[now]==now)return now;
return fa[now]=findd(fa[now]);
}
void vnion(int u,int v){
u=findd(u);v=findd(v);
if(u==v)return;
fa[u]=v;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=2*m;i++)fa[i]=i;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1,k,x;i<=m;i++){
scanf("%d",&k);
for(int j=1;j<=k;j++){
scanf("%d",&x);
g[x].push_back(i);
}
}
for(int i=1;i<=n;i++){
if(a[i]==1){
vnion(g[i][0],g[i][1]);
vnion(g[i][0]+m,g[i][1]+m);
}
else{
vnion(g[i][0],g[i][1]+m);
vnion(g[i][0]+m,g[i][1]);
}
}
for(int i=1;i<=m;i++){
if(findd(i)==findd(i+m)){
printf("NO");
return 0;
}
}
printf("YES");
return 0;
}
```