slope trick 笔记
鲤鱼江
·
·
算法·理论
最近重新看了一遍才觉得这个东西非常之深刻。
网上题解大多都只给出了简化到极致的代码并且没有分析本质,很有误导性。
上下凸是对称的,本文只讲究下凸的维护。
适用情形
处理二维及以上的 DP 时可能会出现一种转移形式,其要求我们前缀取 \min(或者跟前面 x 个数取 \min),然后加减一些东西,朴素地做很可能会是 O(n^2) 的,不可接受。
此时如果我们可以证明 DP 数组的某一维具有凸性,那么就可以使用叫做 slope trick 的手法对该维进行维护从而做到更优秀的复杂度。
基本知识
首先你要知道下凸是啥。
称一个数组是下凸的当且仅当其差分数组单调不降。
下凸的封闭性:
- 两个下凸的数组对位相加依然是下凸的,因为对位相加相当于差分数组也对位相加了。
- 两个下凸的数组做 (\min,+) 卷积(或者说下凸的闵可夫斯基和)之后仍然是下凸的。
证明 $h$ 的凸性是不困难的,我们将 $f$ 和 $g$ 的差分数组归并起来明显是 $h$ 的差分数组。
## naive 的做法
从例题入手吧,感受一下如果使用最 naive 的方法应该要维护哪些东西。
### CF13C
用 $f_{i,j}$ 表示考虑了前 $i$ 个数,第 $i$ 个数 $\le j$ 的最小操作次数,那么明显有 DP 式子:$f_{i,j}=\min_{k\le j}(f_{i-1,k})+|a_i-j|$。
把二维拍扁成一维,思考 $f_i$ 的变化,明显是做一遍前缀取 $\min$,然后加上绝对值函数。
前缀取 $\min$ 相当于和 $\{0,0,\dots\}$ 做闵可夫斯基和,$|a_i-x|$ 明显是下凸的。
所以可以证明 $f$ 任意时刻都是下凸的。
考虑使用下凸壳来刻画 $f$,要做闵可夫斯基和所以不难想到维护 $f$ 的差分,问题转化为了我们要支持插入若干个数和区间加减,$f_0$ 手动维护就行了。
可以使用 FHQ 维护二元组 $(x,y)$ 表示这里有 $y$ 个 $x$。
但是太冗长了,你不需要去实现它,后面会讲更简洁的方法。
### CF1534G
再来感受一道题,CF `*3300` 你值得拥有。
考虑一条从左下到右上的路径,每一个点到这个路径的最短切比雪夫距离一定在与这个点同处于一条斜率为 $-1$ 的点上取到。
从题解贺一张图:
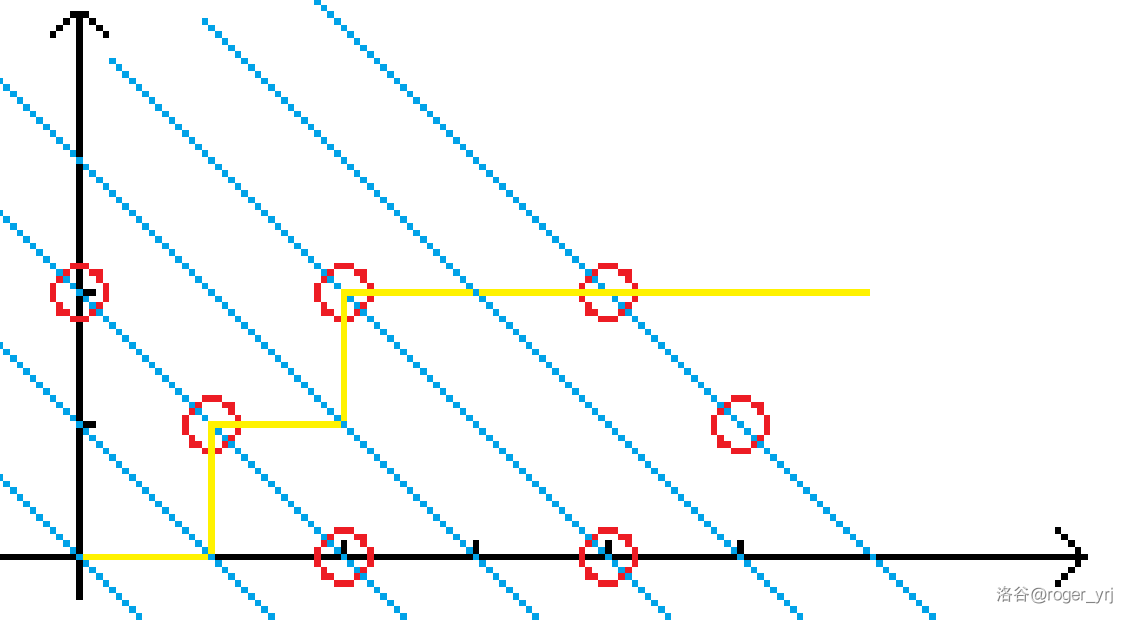
显然此时 $|X-x|=|Y-y|$。
用 $f_{i,j}$ 表示走了 $i$ 步,此时纵坐标为 $j$,种土豆的最小代价。
$f_{i,j}=\min(f_{i-1,j-1},f_{i-1,j})+\sum_{x_k+y_k=i}|j-y_k|$。
操作相当于要跟 $\{0,0\}$ 做闵可夫斯基和,加绝对值函数,不难归纳证明凸性。
常规地维护差分,支持区间加减和插入一个数。
## 优雅的维护方式
想必现在你对 slope trick 有一定理解了,我们思考一下更简洁的做法。
对于一类斜率为整数,值域较小且斜率变化的点很少的下凸函数,比如(再贺一张):

我们采用三元组 $(k,b,S)$ 来刻画,$k,b$ 表示第一段函数为 $kx+b$;$S$ 是拐点可重集,表示若 $d$ 在 $S$ 中出现了 $c$ 次,那么斜率在 $d$ 处增加了 $c$。
比如上面的图所对应的三元组是 $(-2,-3,\{-3,-1,2,6\})$。
那么:两个下凸函数 $(k_0,b_0,S_0)$ 和 $(k_1,b_1,S_1)$ 相加后的函数是 $(k_0+k_1,b_0+b_1,S_0\cup S_1)$。
不难发现这种维护方式可以很方便地完成函数相加或平移,但是似乎并不方便支持闵可夫斯基和。
但是和 $\{0,\dots,0\}$ 做闵可夫斯基和就另当别论了。
我们维护左右凸壳,左凸壳维护斜率 $< 0$ 的部分,右凸壳维护斜率 $>0$ 的部分,那么和 $\{0,\dots,0\}$($c$ 个 $0$)做闵可夫斯基和相当于把右凸壳整体向右移动 $c$ 位,打个懒标记就可以做到了。
### CF13C
不难发现前缀取 $\min$ 等价于直接清空右凸壳,那么我们可以只维护左凸壳,这个想法是自然的。
$|a_i-x|$ 明显是 $(-1,a_i,\{a_i,a_i\})$,然后就可以直接做了,但是还可以更简洁!
维护 $k,b$ 有点麻烦,仔细思考发现,在取前缀 $\min$ 之后 $k=-|S|$,因为我们在 $|S|$ 次 $+1$ 之后得到了最后一段,最后一段斜率明显为 $0$,所以 $k=-|S|$。
$b$ 似乎也可以不维护,因为我们只需要知道函数最小值,所以直接维护在 $0$ 处的取值即可 $w$,明显是 $\sum a_i$。
考虑怎么清空右凸壳,在令 $S=S\cup \{a_i,a_i\}$ 后,最后一段的斜率必然是 $1$,弹掉最大的拐点即可。
最后答案显然是 $\sum\limits_{i=1}^n a_i-\sum\limits_{x\in S}x$,因为我们要求最后一段的纵坐标,明显 $0$ 处取值是 $\sum\limits_{i=1}^n a_i$,而每一个拐点 $x$ 都会产生 $-x$ 的贡献,简单手模一下就知道为什么了。
代码大概长这个样子:
```
for(int i=1;i<=n;++i) cin>>a[i],ans+=a[i];
for(int i=1;i<=n;++i){
Q.push(a[i]);
Q.push(a[i]);
Q.pop();
}
while(!Q.empty()){
ans-=Q.top();
Q.pop();
}
cout<<ans<<'\n';
```
### CF1534G
这个题变成了和 $\{0,0\}$ 闵可夫斯基和,其实相当于把右凸壳向右边平移一格,打个懒标记就行了。
具体来说我们维护两个堆,一个堆维护左凸壳,一个堆维护右凸壳,每次加一个绝对值函数的时候最多会导致一个拐点从左凸壳换到右凸壳,或者从从右凸壳换到左凸壳。