#define ls (p<<1) // 写成 1<<p 痛失 3 罚时
#define rs (p<<1|1)
const int maxn=2e5+5;
long long segtree[maxn<<2]/*注意是 4 倍空间*/,a[maxn],lazy[maxn],n,q;
void pushup(long long l,long long r,long long p){
segtree[p]=segtree[ls]+segtree[rs];
}
void build(long long l,long long r,long long p){
if(l==r){
segtree[p]=a[l];
return;
}
long long mid=l+r>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(l,r,p);
}
接下来是查询:
其实查询的过程就是将小区间合并为大区间。
还是这个图:
```
| 1 | 2 | 3 | 4 | 5 |
|-------------------|
|-----------|-------|
|-------|---|---|---|
|---|---|
|-----------| 要查询的区间为2~4
|-------------------| 有交集,下传
|-----------| 左右都有交集,下传
|-----------|-------|
|-------|---|
|-------|---|---|---| 最后一段没有交集,第二段与第三段是全部包含,第一段有交集,下传
|---| 是第二段的全部
|---|---|
于是就有小区间拼成大区间:
|-------------------|
|-----------|-------|
|-------|===|===|---|
|---|===|
如果是1~4:
|-------------------|
|===========|-------|
|-------|---|===|---|
|---|---|
etc.
```
然后就有代码:
```cpp
long long query(int l,int r,int p,int s,int t){
if(t<l||s>r)return 0;// 避开无交集的区间
if(s<=l&&r<=t)
return segtree[p];
int mid=l+r>>1;
return query(l,mid,ls,s,t)+query(mid+1,r,rs,s,t);
}
```
$O(\log n)$。
接下来是 `add` 函数。
---
单点修:
直接递归到那个点修改:
```cpp
void add(int l,int r,int p,int s,int t){
if(l==r){segtree[p]+=t;return;}
int mid=l+r>>1;
if(s<=mid)add(l,mid,p<<1,s,t);
else add(mid+1,r,p<<1|1,s,t);
pushup(l,r,p);
}
```
$O(\log n)$。
没了。
:::success[[P3374 【模板】树状数组 1 - 洛谷](https://www.luogu.com.cn/problem/P3374) 实现:]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const int maxn=5e5+5;
long long segtree[maxn<<2],a[maxn],lazy[maxn],n,q;
void pushup(long long l,long long r,long long p){
segtree[p]=segtree[ls]+segtree[rs];
}
void build(long long l,long long r,long long p){
if(l==r){
segtree[p]=a[l];
return;
}
long long mid=l+r>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(l,r,p);
}
long long query(int l,int r,int p,int s,int t){
if(t<l||s>r)return 0;
if(s<=l&&r<=t)
return segtree[p];
int mid=l+r>>1;
return query(l,mid,ls,s,t)+query(mid+1,r,rs,s,t);
}
void add(int l,int r,int p,int s,int t){
if(l==r){segtree[p]+=t;return;}
int mid=l+r>>1;
if(s<=mid)add(l,mid,p<<1,s,t);
else add(mid+1,r,p<<1|1,s,t);
segtree[p]=segtree[p<<1]+segtree[p<<1|1];
}
int main(){
cin>>n>>q;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,n,1);
while(q--){
int op,x,y;
cin>>op>>x>>y;
if(op==1)add(1,n,1,x,y);
else cout<<query(1,n,1,x,y)<<"\n";
}
return 0;
}
```
:::
---
区间修改:
### lazy tag
lazy tag,即懒标记,指在修改时找到一个包含的线段即可将其修改、打上懒标记,表示当前修改了 $lazy_{p}$ 个偏移量未下传,即分下去的线段还没有偏移,不用再下传造成 $O(len\log n)$ 的时间,而到了查询或修改时区间不完全被包含再下传懒标记,就是左右儿子的 `segtree` 数组。
然后没了,记得在 `query` 时也要 `pushdown`!
:::success[[P3372 【模板】线段树 1 - 洛谷](https://www.luogu.com.cn/problem/P3372) 实现:]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const long long maxn=2e5+5;
long long segtree[maxn<<2],a[maxn],lazy[maxn],n,q;
void pushup(long long l,long long r,long long p){
segtree[p]=segtree[ls]+segtree[rs];
}
void pushdown(long long l,long long r,long long p){
lazy[ls]+=lazy[p];
lazy[rs]+=lazy[p];
segtree[ls]+=((l+r>>1)-l+1)*lazy[p];
segtree[rs]+=(r-(l+r>>1))*lazy[p];
lazy[p]=0;
}
void build(long long l,long long r,long long p){
if(l==r){
segtree[p]=a[l];
return;
}
long long mid=l+r>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(l,r,p);
}
void add(long long l,long long r,long long p,long long s,long long t,long long v){
if(t<l||s>r)return;
if(s<=l&&r<=t){
lazy[p]+=v;
segtree[p]+=(r-l+1)*v;
return;
}
pushdown(l,r,p);
long long mid=l+r>>1;
add(l,mid,ls,s,t,v);
add(mid+1,r,rs,s,t,v);
pushup(l,r,p);
}
long long query(long long l,long long r,long long p,long long s,long long t){
if(t<l||s>r)return 0;
if(s<=l&&r<=t)
return segtree[p];
pushdown(l,r,p);
long long mid=l+r>>1;
return query(l,mid,ls,s,t)+query(mid+1,r,rs,s,t);
}
int main(){
cin>>n>>q;
for(long long i=1;i<=n;i++)cin>>a[i];
build(1,n,1);
while(q--){
long long op,l,r;
cin>>op>>l>>r;
if(op==1){
long long x;
cin>>x;
add(1,n,1,l,r,x);
}else{
cout<<query(1,n,1,l,r)<<"\n";
}
}
return 0;
}
```
:::
## 看例题
### [P3373 【模板】线段树 2 - 洛谷](https://www.luogu.com.cn/problem/P3373)
毒瘤,但只是 `pushdown` 多亿点点而已。
考虑乘法懒标记下传。
左右儿子的乘法懒标记、加法懒标记、和都乘上当前乘法懒标记。
加法同上。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const long long maxn=2e5+5;
long long segtree[maxn<<2],a[maxn],lazy[maxn<<2],mul[maxn<<2],n,q,m,pos[maxn];
void pushup(long long l,long long r,long long p){
segtree[p]=segtree[ls]+segtree[rs];
segtree[p]%=m;
}
void pushdown(long long l,long long r,long long p){
if(mul[p]!=1){
lazy[ls]*=mul[p];lazy[ls]%=m;
lazy[rs]*=mul[p];lazy[rs]%=m;
mul[ls]*=mul[p];mul[ls]%=m;
mul[rs]*=mul[p];mul[rs]%=m;
segtree[ls]*=mul[p];segtree[ls]%=m;
segtree[rs]*=mul[p];segtree[rs]%=m;
mul[p]=1;
}
if(lazy[p]!=0){
lazy[ls]+=lazy[p];lazy[ls]%=m;
lazy[rs]+=lazy[p];lazy[rs]%=m;
segtree[ls]+=lazy[p]*((l+r>>1)-l+1);segtree[ls]%=m;
segtree[rs]+=lazy[p]*(r-(l+r>>1));segtree[rs]%=m;
lazy[p]=0;
}
}
void build(long long l,long long r,long long p){
if(l==r){
segtree[p]=a[l];
return;
}
long long mid=l+r>>1;
mul[p]=1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(l,r,p);
}
void add(long long l,long long r,long long p,long long s,long long t,long long v){
if(t<l||s>r)return;
if(s<=l&&r<=t){
lazy[p]+=v;lazy[p]%=m;
segtree[p]+=(r-l+1)*v;segtree[p]%=m;
return;
}
pushdown(l,r,p);
long long mid=l+r>>1;
add(l,mid,ls,s,t,v);
add(mid+1,r,rs,s,t,v);
pushup(l,r,p);
}
void multi(long long l,long long r,long long p,long long s,long long t,long long v){
if(t<l||s>r)return;
if(s<=l&&r<=t){
mul[p]*=v;mul[p]%=m;
lazy[p]*=v;lazy[p]%=m;
segtree[p]*=v;segtree[p]%=m;
return;
}
pushdown(l,r,p);
long long mid=l+r>>1;
multi(l,mid,ls,s,t,v);
multi(mid+1,r,rs,s,t,v);
pushup(l,r,p);
}
long long query(long long l,long long r,long long p,long long s,long long t){
if(t<l||s>r)return 0;
if(s<=l&&r<=t)
return segtree[p];
pushdown(l,r,p);
long long mid=l+r>>1;
return(query(l,mid,ls,s,t)+query(mid+1,r,rs,s,t))%m;
}
int main(){
cin>>n>>q>>m;
for(long long i=1;i<=n;i++)cin>>a[i];
build(1,n,1);
while(q--){
long long op,l,r;
cin>>op>>l>>r;
if(op==2){
long long x;
cin>>x;
add(1,n,1,l,r,x);
}else if(op==1){
long long x;
cin>>x;
multi(1,n,1,l,r,x);
}else{
cout<<query(1,n,1,l,r)<<"\n";
}
}
return 0;
}
```
:::
### [P1531 I Hate It - 洛谷](https://www.luogu.com.cn/problem/P1531)
维护最大值区间。这题不用 lazy tag,但是我还是打了。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
const long long maxn=2e5+5;
long long segtree[maxn<<2],a[maxn],lazy[maxn<<1],n,q;
void pushup(int l,int r,int p){
segtree[p]=max(segtree[ls],segtree[rs]);
}
void pushdown(int l,int r,int p){
lazy[ls]=max(lazy[ls],lazy[p]);
lazy[rs]=max(lazy[rs],lazy[p]);
segtree[ls]=max(segtree[ls],lazy[p]);
segtree[rs]=max(segtree[rs],lazy[p]);
lazy[p]=0;
}
void build(int l,int r,int p){
if(l==r){
segtree[p]=a[l];
return;
}
int mid=l+r>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(l,r,p);
}
void add(int l,int r,int p,long long s,long long t,long long v){
if(t<l||s>r)return;
if(s<=l&&r<=t){
lazy[p]=max(lazy[p],v);
segtree[p]=max(segtree[p],v);
return;
}
pushdown(l,r,p);
int mid=l+r>>1;
add(l,mid,ls,s,t,v);
add(mid+1,r,rs,s,t,v);
pushup(l,r,p);
}
long long query(int l,int r,int p,long long s,long long t){
if(t<l||s>r)return 0;
if(s<=l&&r<=t)
return segtree[p];
pushdown(l,r,p);
int mid=l+r>>1;
return max(query(l,mid,ls,s,t),query(mid+1,r,rs,s,t));
}
int main(){
cin>>n>>q;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,n,1);
while(q--){
char op;
int l,r;
cin>>op>>l>>r;
if(op=='U'){
add(1,n,1,l,l,r);
}else{
cout<<query(1,n,1,l,r)<<"\n";
}
}
return 0;
}
```
:::
# 动态开点线段树
有些区间无需查询,那么就动态开点,需要查一个就开一个。
每次加点都是 $O(\log n)$ 级别的,总共 $O(q\log n)$,没必要开 $O(n\log n)$ 个点,只需要在 `add()` 时传递下去即可。`query()` 根本不用管没开的节点。空的就返回 $0$。
## [P13825 【模板】线段树 1.5 - 洛谷](https://www.luogu.com.cn/problem/P13825)
这题……$n\le 10^9$,只能上动态开点。
`add()` 如果要懒标记下传,那么新开左右儿子存下懒标记;
:::success[Template]
```cpp
template<typename T>
class segtree{
T L,R;
struct node{
T sum{},ls{},rs{},lazy{};
};
vector<node>tree;
void pushdown(T l,T r,int p,bool b=true){
if(b!=0){
if(!tree[p].ls)tree[p].ls=tree.size(),tree.emplace_back();
if(!tree[p].rs)tree[p].rs=tree.size(),tree.emplace_back();
if(!tree[p].lazy)return;
T mid=l+r>>1;
tree[tree[p].ls].sum+=(mid-l+1)*tree[p].lazy;
tree[tree[p].rs].sum+=(r-mid)*tree[p].lazy;
tree[tree[p].ls].lazy+=tree[p].lazy;
tree[tree[p].rs].lazy+=tree[p].lazy;
tree[p].lazy=0;
}else{
T mid=l+r>>1;
if(tree[p].ls){
tree[tree[p].ls].sum+=(mid-l+1)*tree[p].lazy;
tree[tree[p].ls].lazy+=tree[p].lazy;
}
if(tree[p].rs){
tree[tree[p].rs].sum+=(mid-l+1)*tree[p].lazy;
tree[tree[p].rs].lazy+=tree[p].lazy;
}
}
}
void pushup(int p){
tree[p].sum=0;
if(tree[p].ls)tree[p].sum+=tree[tree[p].ls].sum;
if(tree[p].rs)tree[p].sum+=tree[tree[p].rs].sum;
}
void add(T l,T r,int p,T s,T t,T c){
if(!p||l>t||r<s)return;
if(s<=l&&r<=t){
tree[p].sum+=(r-l+1)*c,tree[p].lazy+=c;
return;
}
pushdown(l,r,p);
T mid=l+r>>1;
add(l,mid,tree[p].ls,s,t,c);
add(mid+1,r,tree[p].rs,s,t,c);
pushup(p);
}
T query(T l,T r,int p,T s,T t){
if(!p||l>t||r<s)return 0;
if(s<=l&&r<=t)return tree[p].sum;
T mid=l+r>>1;
T ans=0;
pushdown(l,r,p,0);
ans+=query(l,mid,tree[p].ls,s,t);
ans+=query(mid+1,r,tree[p].rs,s,t);
return ans;
}
public:
segtree():L(numeric_limits<T>::min()),R(numeric_limits<T>::max()){tree=vector<node>(2);}
segtree(T l,T r):L(l),R(r){tree=vector<node>(2);}
void add(T l,T r,T c){
add(L,R,1,l,r,c);
}
T query(T l,T r){
return query(L,R,1,l,r);
}
};
segtree<int>sgtree;
```
:::
## [P3184 [USACO16DEC] Counting Haybales S - 洛谷](https://www.luogu.com.cn/problem/P3184)
杀鸡用宰牛刀。
(甚至不需要 `add()`)
```cpp
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>q;
for(int i=1;i<=n;i++){
int x;
cin>>x;
sgtree.add(x,x,1);
}
for(int i=1;i<=q;i++){
int l,r;
cin>>l>>r;
cout<<sgtree.query(l,r)<<"\n";
}
return 0;
}
```
## [P13825 【模板】线段树 1.5 - 洛谷](https://www.luogu.com.cn/problem/P13825)
板题。
:::warning[Trick]{open}
要开 `ull`。
:::
```cpp
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>q;
for(int i=1;i<=q;i++){
int op;
cin>>op;
ull l,r,k;
if(op==1){
cin>>l>>r>>k;
sgtree.add(l,r,k);
}else{
cin>>l>>r;
cout<<sgtree.query(l,r)+(l+r)*(r-l+1)/2<<"\n";
}
}
return 0;
}
```
---
重点在主席树。
# 主席树
接下来是主席树(其实是可持久化线段树)。
## 先上板题[P3919 【模板】可持久化线段树 1(可持久化数组) - 洛谷](https://www.luogu.com.cn/problem/P3919)。
### 思路
考虑如何更新。更新是一大重点。
每次更新一个节点。
一个节点。为什么?
增加严格 $O(\log n)$ 个节点吗?
不用 $lazy$ 数组吗?
考虑增加严格 $O(\log n)$ 个节点。
> 重建一棵线段树?
>
> $O(\log n)$ 个节点被改变,未免太过浪费。
>
> 那么只更新 $O(\log n)$ 个节点,剩下的线段树不动?
>
> 嗯对!就这么干!
新建一个根节点,连上不动的旧节点为左或右儿子(原来是左儿子就是左儿子,原来是右儿子就是右儿子),剩下那个儿子新建一个节点出来就好了。
如 OI-Wiki 图:
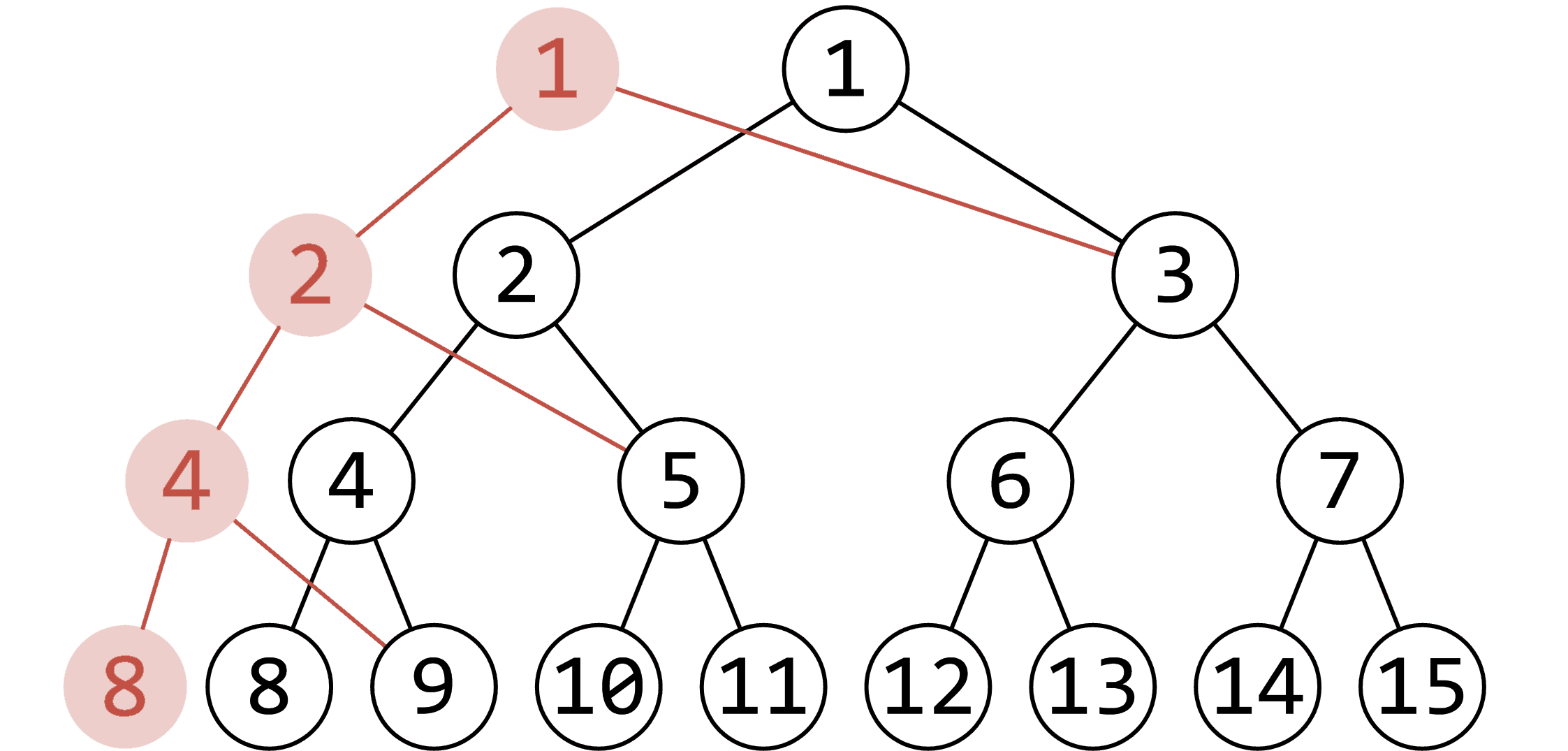
就是新开一条链。
在上面的代码上改改就好了。
没写模板,见谅。
:::success[Template]
```cpp
class psegtree{
struct pnode{
ll sum{},ls{},rs{};
};
vector<pnode>tree;
vector<int>rt;
int newrt(int t){
rt.push_back({t});
return rt.size()-1;
}
int newnode(){
tree.push_back({});
return tree.size()-1;
}
void pushup(int p){
tree[p].sum=0;
if(tree[p].ls)tree[p].sum+=tree[tree[p].ls].sum;
if(tree[p].rs)tree[p].sum+=tree[tree[p].rs].sum;
}
void add(int lst,int l,int r,int p,int x,int c){
if(l==r){
tree[p].sum/*+*/=c;// 若是修改就要两个 qwq 行
return;
}
int mid=l+r>>1;
if(x<=mid){
tree[p].ls=newnode();
// tree[tree[p].ls].sum=tree[tree[lst].ls].sum; // qwq
tree[p].rs=tree[lst].rs;
add(tree[lst].ls,l,mid,tree[p].ls,x,c);
}else{
tree[p].rs=newnode();
// tree[tree[p].rs].sum=tree[tree[lst].rs].sum; // qwq
tree[p].ls=tree[lst].ls;
add(tree[lst].rs,mid+1,r,tree[p].rs,x,c);
}
pushup(p);
}
ll query(int l,int r,int p,int s,int t){
if(!p||l>t||r<s)return 0;
if(s<=l&&r<=t)return tree[p].sum;
int mid=l+r>>1;
ll ans=0;
ans+=query(l,mid,tree[p].ls,s,t);
ans+=query(mid+1,r,tree[p].rs,s,t);
return ans;
}
public:
psegtree(){
newnode();
newrt(newnode());
}
void add(int k,int x,int c){
int p=newrt(newnode());
add(rt[k],0,1e9,rt[p],x,c);
}
ll query(int k,int l,int r){
int p=newrt(rt[k]);// qaq 这个标记后面会用到
return query(0,1e9,rt[p],l,r);
}
};
```
这题还要 `build()`。
```cpp
void build(int l,int r,int p){
if(l==r){
tree[p].sum=a[l];
return;
}
int mid=l+r>>1;
build(l,mid,tree[p].ls=newnode());
build(mid+1,r,tree[p].rs=newnode());
pushup(p);
}
```
:::
## [P3834 【模板】可持久化线段树 2 - 洛谷](https://www.luogu.com.cn/problem/P3834)
主席树,全称可持久化权值线段树。
权值,指某个值出现的次数。主席树维护区间内每个数出现的次数。
一个一个加,就成了前缀和。
至于找第 $k$ 大,线段树上二分!
:::info[如何线段树上二分?]
嗯对,线段树内部维护了区间和,如上做差分判断是否大于 $k$ 为 `check`。
:::
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int n,q,a[maxn];
typedef long long ll;
template<typename T>
class psegtree{
struct pnode{
ll sum{},ls{},rs{};
};
vector<pnode>tree;
vector<int>rt;
int newrt(int t){
rt.push_back({t});
return rt.size()-1;
}
int newnode(){
tree.push_back({});
return tree.size()-1;
}
void pushup(int p){
tree[p].sum=0;
if(tree[p].ls)tree[p].sum+=tree[tree[p].ls].sum;
if(tree[p].rs)tree[p].sum+=tree[tree[p].rs].sum;
}
void add(int lst,int l,int r,int p,int x,int c){
if(l==r){
tree[p].sum+=c;
return;
}
int mid=l+r>>1;
if(x<=mid){
tree[p].ls=newnode();
tree[tree[p].ls].sum=tree[tree[lst].ls].sum;
tree[p].rs=tree[lst].rs;
add(tree[lst].ls,l,mid,tree[p].ls,x,c);
}else{
tree[p].rs=newnode();
tree[tree[p].rs].sum=tree[tree[lst].rs].sum;
tree[p].ls=tree[lst].ls;
add(tree[lst].rs,mid+1,r,tree[p].rs,x,c);
}
pushup(p);
}
ll query(int l,int r,int p,int s,int t){
if(!p||l>t||r<s)return 0;
if(s<=l&&r<=t)return tree[p].sum;
int mid=l+r>>1;
ll ans=0;
ans+=query(l,mid,tree[p].ls,s,t);
ans+=query(mid+1,r,tree[p].rs,s,t);
return ans;
}
ll kth(int l,int r,int L,int R,int pl,int pr,int k){// 线段树上二分
if(L==R)return L;// 边界
int M=L+R>>1;
if(tree[tree[pr].ls].sum-tree[tree[pl].ls].sum>=k)return kth(l,r,L,M,tree[pl].ls,tree[pr].ls,k);// 差分
return kth(l,r,M+1,R,tree[pl].rs,tree[pr].rs,k-(tree[tree[pr].ls].sum-tree[tree[pl].ls].sum));
}
public:
psegtree(){
newnode();
newrt(newnode());
}
void add(int k,int x,int c){
int p=newrt(newnode());
add(rt[k],0,1e9,rt[p],x,c);
}
ll query(int k,int l,int r){
int p=newrt(rt[k]);
return query(0,1e9,rt[p],l,r);
}
ll kth(int l,int r,int k){
return kth(l-1,r,0,1e9,rt[l-1],rt[r],k);
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n>>q;
psegtree<ll>sgt;
for(int i=1;i<=n;i++)
cin>>a[i],sgt.add(i-1,a[i],1);
while(q--){
int l,r,k;
cin>>l>>r>>k;
cout<<sgt.kth(l,r,k)<<"\n";
}
return 0;
}
```
:::
### [P3755 [CQOI2017] 老C的任务 - 洛谷](https://www.luogu.com.cn/problem/P3755)
先离散化。
主席树一个一个加,就当 $x_i$ 是 $i$,`sgtree.add(i-1,y,p)`。
然后就没有然后了。
查询时二分边界,而后差分查找。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int n,q;
typedef long long ll;
struct pnode{
ll sum{},ls{},rs{};
};
class psegtree{
vector<pnode>tree;
vector<int>rt;
int newrt(int t){
rt.push_back({t});
return rt.size()-1;
}
int newnode(){
tree.push_back({});
return tree.size()-1;
}
void pushup(int p){
tree[p].sum=0;
if(tree[p].ls)tree[p].sum+=tree[tree[p].ls].sum;
if(tree[p].rs)tree[p].sum+=tree[tree[p].rs].sum;
}
void add(int lst,int l,int r,int p,int x,int c){
if(l==r){
tree[p].sum+=c;
return;
}
int mid=l+r>>1;
if(x<=mid){
tree[p].ls=newnode();
tree[tree[p].ls].sum=tree[tree[lst].ls].sum;
tree[p].rs=tree[lst].rs;
add(tree[lst].ls,l,mid,tree[p].ls,x,c);
}else{
tree[p].rs=newnode();
tree[tree[p].rs].sum=tree[tree[lst].rs].sum;
tree[p].ls=tree[lst].ls;
add(tree[lst].rs,mid+1,r,tree[p].rs,x,c);
}
pushup(p);
}
ll query(int l,int r,int p,int s,int t){
if(!p||l>t||r<s)return 0;
if(s<=l&&r<=t)return tree[p].sum;
int mid=l+r>>1;
ll ans=0;
ans+=query(l,mid,tree[p].ls,s,t);
ans+=query(mid+1,r,tree[p].rs,s,t);
return ans;
}
ll kth(int l,int r,int L,int R,int pl,int pr,int k){
if(L==R)return L;
int M=L+R>>1;
if(tree[tree[pr].ls].sum-tree[tree[pl].ls].sum>=k)return kth(l,r,L,M,tree[pl].ls,tree[pr].ls,k);
return kth(l,r,M+1,R,tree[pl].rs,tree[pr].rs,k-(tree[tree[pr].ls].sum-tree[tree[pl].ls].sum));
}
public:
psegtree(){
newnode();
newrt(newnode());
}
void add(int k,int x,int c){
int p=newrt(newnode());
add(rt[k],INT_MIN,INT_MAX,rt[p],x,c);
}
ll query(int k,int x,int c){
int p=newrt(rt[k]);
return query(INT_MIN,INT_MAX,rt[p],x,c);
}
ll kth(int l,int r,int k){
return kth(l-1,r,INT_MIN,INT_MAX,rt[l-1],rt[r],k);
}
};
tuple<int,int,int>a[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>n>>q;
psegtree sgt;
for(int i=1;i<=n;i++)
cin>>get<0>(a[i])>>get<1>(a[i])>>get<2>(a[i]);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++){
auto[x,y,z]=a[i];
sgt.add(i-1,y,z);
}
while(q--){
int l,r,u,d;
cin>>u>>l>>d>>r;
int Left=lower_bound(a+1,a+1+n,make_tuple(u,0,0))-a-1;// 左端点减 1 是差分的
int Right=upper_bound(a+1,a+1+n,make_tuple(d,INT_MAX,INT_MAX))-a-1;// 右端点减 1 是 upper_bound 的
cout<<sgt.query(Right,l,r)-sgt.query(Left,l,r)<<"\n";
}
return 0;
}
```
:::
### [P1383 高级打字机 - 洛谷](https://www.luogu.com.cn/problem/P1383)
简单维护一下每个文本的长度就好。
因为 `Q` 不算修改,所以将板子的 `qaq` 行删除。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int q;
vector<int>length;
typedef long long ll;
class psegtree{
struct pnode{
ll sum{},ls{},rs{};
};
vector<pnode>tree;
vector<int>rt;
int newrt(int t){
rt.push_back({t});
return rt.size()-1;
}
int newnode(){
tree.push_back({});
return tree.size()-1;
}
void pushup(int p){
tree[p].sum=0;
if(tree[p].ls)tree[p].sum+=tree[tree[p].ls].sum;
if(tree[p].rs)tree[p].sum+=tree[tree[p].rs].sum;
}
void add(int lst,int l,int r,int p,int x,int c){
if(l==r){
tree[p].sum=c;
return;
}
int mid=l+r>>1;
if(x<=mid){
tree[p].ls=newnode();
tree[p].rs=tree[lst].rs;
add(tree[lst].ls,l,mid,tree[p].ls,x,c);
}else{
tree[p].rs=newnode();
tree[p].ls=tree[lst].ls;
add(tree[lst].rs,mid+1,r,tree[p].rs,x,c);
}
pushup(p);
}
ll query(int l,int r,int p,int s,int t){
if(!p||l>t||r<s)return 0;
if(s<=l&&r<=t)return tree[p].sum;
int mid=l+r>>1;
ll ans=0;
ans+=query(l,mid,tree[p].ls,s,t);
ans+=query(mid+1,r,tree[p].rs,s,t);
return ans;
}
public:
psegtree(){
newnode();
newrt(newnode());
}
void add(int k,int x,int c){
int p=newrt(newnode());
add(rt[k],1,114514,rt[p],x,c);
}
ll query(int k,int x,int c){
return query(1,114514,rt[k],x,c);
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
cin>>q;
length.push_back(0);
psegtree sgt;
while(q--){
char op;
cin>>op;
if(op=='U'){
int k;
cin>>k;
int lst=length.size()-k-1;
sgt.add(lst,length[lst]+1,0);
length.push_back(length[lst]);
}else if(op=='T'){
char k;
cin>>k;
int lst=length.size()-1;
sgt.add(lst,length[lst]+1,k);
length.push_back(length[lst]+1);
}else{
int k;
cin>>k;
cout<<char(sgt.query(length.size()-1,k,k))<<"\n";
}
}
return 0;
}
```
:::
# 线段树合并
一个很有意思的算法。
## 先看一道经典例题[P3201 [HNOI2009] 梦幻布丁 - 洛谷](https://www.luogu.com.cn/problem/P3201)
考虑暴力地线段树。
开 $10^6$ 棵线段树,存下每个颜色所在的所有位置(这你要不动态开点就会有大大的 $\Large\colorbox{#052242}{\color{white}MLE}$),然后修改直接暴力一个一个删、一个一个加过去。
> 定义有点抽象,举个例子。
>
> 比如 $a=\{1,1,4,5,1,4\}$,那么就 `add(1,6,rt[1],1,1),add(1,6,rt[1],2,1),add(1,6,rt[4],3,1),add(1,6,rt[5],4,1),add(1,6,rt[1],5,1),add(1,6,rt[4],6,1);`($rt_i$ 表示第 $i$ 棵线段树的根)。
如何求答案呢?设 $cl$ 为区间左端点,$cr$ 为区间右端点颜色,$ans$ 为区间颜色段数,那么 $ans_i=ans_{lson_i}+ans_{rson_i}-[cr_{lson_i}=1\text{ 且 }cl_{lson_i}=1]$。最终答案就是 $\sum ans_{rt_i}$。
求答案就是 `pushup`,但是修改就成了 $O(\log^2n)$ 的了。
如何变成 $O(\log n)$ 的呢?
想到每个位置一一可以对应,那么可以一一对应地 `dfs`。
形式化地说,就是存两种颜色的下标,合并时直接挪过来就好,不用再 `dfs`。
然后就有了 `merge`。
```cpp
int merge(int p0,int p1,int l,int r){
if(!p0||!p1)return p0|p1;
if(l==r){
cl[p0]|=cl[p1];// 有一个点有就行
cr[p0]|=cr[p1];
ans[p0]=cl[p0];// 实际上就是如果有,ans[p0]=1,否则 ans[p0]=0;
// do something...
return p0;
}
int mid=l+r>>1;
ls[p0]=merge(ls[p0],ls[p1],l,mid);
rs[p0]=merge(rs[p0],rs[p1],mid+1,r);
pushup(p0);
return p0;
}
```
:::warning[Trick]{open}
会有 $x=y$ 的情况!
:::
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=4e6+5;
int ans[maxn],cl[maxn],cr[maxn],ls[maxn],rs[maxn],n,cnt,rt[maxn],m,mxcolor,sum;
void pushup(int p){
cl[p]=cl[ls[p]];
cr[p]=cr[rs[p]];
ans[p]=ans[ls[p]]+ans[rs[p]]-(cr[ls[p]]&&cl[rs[p]]);
}
void add(int l,int r,int p,int x){
if(l==r){
cl[p]=cr[p]=ans[p]=1;
return;
}
int mid=l+r>>1;
if(x<=mid){
if(!ls[p])ls[p]=++cnt;
add(l,mid,ls[p],x);
}else{
if(!rs[p])rs[p]=++cnt;
add(mid+1,r,rs[p],x);
}
pushup(p);
}
int query(){
return sum;
}
int merge(int p0,int p1,int l,int r){
if(!p0||!p1)return p0|p1;
if(l==r){
cl[p0]|=cl[p1];// 有一个点有就行
cr[p0]|=cr[p1];
ans[p0]=cl[p0];// 实际上就是如果有,ans[p0]=1,否则 ans[p0]=0。
return p0;
}
int mid=l+r>>1;
ls[p0]=merge(ls[p0],ls[p1],l,mid);
rs[p0]=merge(rs[p0],rs[p1],mid+1,r);
pushup(p0);
return p0;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin>>n>>m;
for(int i=1,x;i<=n;i++)cin>>x,add(1,n,rt[x]=(rt[x]==0?++cnt:rt[x]),i);
for(int i=1;i<=1e6+1;i++)sum+=ans[rt[i]];
while(m--){
int op;
cin>>op;
if(op==1){
int x,y;
cin>>x>>y;
if(x==y)continue;
sum-=ans[rt[y]],sum-=ans[rt[x]];
rt[y]=merge(rt[x],rt[y],1,n);
sum+=ans[rt[y]];
rt[x]=0;
}else{
cout<<query()<<"\n";
}
}
return 0;
}
```
:::
## [P4556 【模板】线段树合并 / [Vani有约会] 雨天的尾巴 - 洛谷](https://www.luogu.com.cn/problem/P4556)
前置知识:[P3128 [USACO15DEC] Max Flow P - 洛谷](https://www.luogu.com.cn/problem/P3128)。
这个差分好像啊。
设 $sum$ 表示区间(粮食编号区间)粮食最大值,$mx$ 表示区间粮食最大值对应最小编号。
然后就是差分了。
合并的 `// do something...` 部分就是 `sum[p0]+=sum[p1];`,因为当前是一个点,这个点当然是求和呀。
然后没了。
蓝板子加绿板子等于紫板子。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=5e6+5;
int sum[maxn],mx[maxn],ls[maxn],rs[maxn],n,cnt,rt[maxn],m;
int anc[maxn][20];
int dep[maxn];
vector<int>G[maxn];
void pushup(int p){
if(sum[ls[p]]>=sum[rs[p]]){
sum[p]=sum[ls[p]];
mx[p]=mx[ls[p]];
}else{
sum[p]=sum[rs[p]];
mx[p]=mx[rs[p]];
}
}
void add(int l,int r,int p,int x,int c){
if(l==r){
sum[p]+=c;
mx[p]=x;
return;
}
int mid=l+r>>1;
if(x<=mid){
if(!ls[p])ls[p]=++cnt;
add(l,mid,ls[p],x,c);
}else{
if(!rs[p])rs[p]=++cnt;
add(mid+1,r,rs[p],x,c);
}
pushup(p);
}
int merge(int p0,int p1,int l,int r){
if(!p0||!p1)return p0|p1;
if(l==r){
sum[p0]+=sum[p1];
return p0;
}
int mid=l+r>>1;
ls[p0]=merge(ls[p0],ls[p1],l,mid);
rs[p0]=merge(rs[p0],rs[p1],mid+1,r);
pushup(p0);
return p0;
}
void dfs(int c,int fa){
dep[c]=dep[fa]+1;
anc[c][0]=fa;
for(int i=1;i<20;i++){
anc[c][i]=anc[anc[c][i-1]][i-1];
}
for(auto i:G[c]){
if(i!=fa){
dfs(i,c);
}
}
}
int lca(int u,int v){
if(dep[u]>dep[v])swap(u,v);
int y=dep[v]-dep[u],cnt=0;
while(y){
if(y&1)v=anc[v][cnt];
++cnt;
y>>=1;
}
if(u==v)return u;
for(int i=19;i>=0;i--){
if(anc[u][i]!=anc[v][i]){
u=anc[u][i];
v=anc[v][i];
}
}
return anc[u][0];
}
void getans(int u,int fa){
for(auto v:G[u]){
if(v==fa)continue;
getans(v,u);
rt[u]=merge(rt[u],rt[v],1,114514);
}
if(!sum[rt[u]])mx[rt[u]]=0;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin>>n>>m;
iota(rt+1,rt+1+n,1);
cnt=n;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(1,0);
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add(1,114514,rt[u],w,1);
add(1,114514,rt[v],w,1);
add(1,114514,rt[lca(u,v)],w,-1);
add(1,114514,rt[anc[lca(u,v)][0]],w,-1);
}
getans(1,0);
for(int i=1;i<=n;i++)cout<<mx[rt[i]]<<"\n";
return 0;
}
```
:::
# 线段树分治
~~lg 的题目有点难,看 loj 的题。~~
[直接看题](https://loj.ac/p/121)。
我们想到离线维护边存在时间的区间。
对时间开一棵线段树,每个节点存当前节点存在的边的编号。~~当然没有 `query`,所以不用 lazy tag。~~
那么怎么处理答案呢?
直接像遍历线段树一样遍历下去,对于一个节点,先加上这个节点保存的所有边,再往下遍历,最后删除当前节点储存的边。如果当前节点储存的 $l$ 等于 $r$ 并且在此处有查询,那么就先加边,再查询。
问题来了:怎么加边、查询、删边?
查询连通性,肯定用并查集啊。
加边也好,怎么删边?
其实就是维护上一次加的边的栈,将连接的两个 `fa` 压栈,出战直接断开联系就好。注意不能路径压缩,只能按秩合并(或启发式合并)。
:::success[AC code && [AC submission](https://loj.ac/s/2497433)]
```cpp
#include<bits/stdc++.h>
using namespace std;
#ifdef ONLINE_JUDGE
#define debug(x)
#else
#define debug(x) cout<<"In function "<<__FUNCTION__<<" "<<#x<<"="<<x<<"\n";
#endif
int n,m;
class Segtree{
int n;
public:
vector<vector<array<int,2>>>tree;
Segtree(int _n):n(_n+3){
tree.assign(n<<2,decltype(tree)::value_type());
}
void add(int l,int r,int p,int L,int R,array<int,2>tim){
if(L>r||R<l)return;
if(L<=l&&r<=R){
tree[p].emplace_back(tim);
return;
}
int mid=l+r>>1;
add(l,mid,p<<1,L,R,tim);
add(mid+1,r,p<<1|1,L,R,tim);
}
};
class DSU{
vector<int>f;
vector<int>d;
stack<tuple<int,int,int>>stk;
public:
DSU(int _n){
f.resize(_n+3);
d.resize(_n+3);
iota(f.begin(),f.end(),0);
fill(d.begin(),d.end(),1);
}
int find(int x){
return f[x]==x?x:find(f[x]);
}
bool unite(int x,int y){
x=find(x),y=find(y);
if(x==y)return false;
if(d[x]>d[y])swap(x,y);
f[x]=y;
stk.push({x,y,d[y]});
d[y]=max(d[y],d[x]+1);
return true;
}
void erase(){
auto[x,y,D]=stk.top();
stk.pop();
f[x]=x;
d[y]=D;
}
};
map<array<int,2>,int>mp;
vector<array<int,2>>query;
void solve(Segtree&sgt,DSU&dsu,vector<char>&now,int l,int r,int p){
if(l==r){
if(query[l][0]){
int cnt=0;
for(auto[x,y]:sgt.tree[p])cnt+=dsu.unite(x,y);
debug(query[l][0])
debug(query[l][1])
debug(dsu.find(query[l][0]))
debug(dsu.find(query[l][1]))
now.emplace_back(dsu.find(query[l][0])==dsu.find(query[l][1])?'Y':'N');
while(cnt--)dsu.erase();
}
return;
}
int cnt=0;
for(auto[x,y]:sgt.tree[p])cnt+=dsu.unite(x,y);
int mid=l+r>>1;
solve(sgt,dsu,now,l,mid,p<<1);
solve(sgt,dsu,now,mid+1,r,p<<1|1);
while(cnt--)dsu.erase();
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin>>n>>m;
DSU dsu(n);
Segtree sgt(m);
query.assign(m+1,{});
for(int i=1;i<=m;i++){
int op,l,r;
cin>>op>>l>>r;
if(l>r)swap(l,r);
if(op==0)
mp[{l,r}]=i;
if(op==1){
sgt.add(1,m,1,mp[{l,r}],i,{l,r});
mp.erase({l,r});
}
if(op==2){
query[i]={l,r};
}
}
for(auto[x,y]:mp)sgt.add(1,m,1,y,m,{x[0],x[1]});
vector<char>ans;
solve(sgt,dsu,ans,1,m,1);
for(auto i:ans)cout<<i<<"\n";
return 0;
}
```
:::
## [P5787 【模板】线段树分治 / 二分图](https://www.luogu.com.cn/problem/P5787)
这原来是二分图模板。。。
前置知识:并查集解决二分图问题。
大家都知道扩展域并查集可以判断二分图,那就再传一个 `flag` 表示当前判断是不是已经不是二分图,如果当前已经不是二分图了,再无论如何也拯救不回来,所以要用 `|=` 判。
依旧并查集加线段树。
:::success[AC code]
```cpp
#include<bits/stdc++.h>
using namespace std;
#ifdef ONLINE_JUDGE
#define debug(x)void(114514)
#else
#define debug(x)cout<<"In function "<<__FUNCTION__<<" "<<#x<<"="<<(x)<<"\n"
#endif
int n,m,k;
class Segtree{
int n;
public:
vector<vector<array<int,2>>>tree;
Segtree(int _n):n(_n+3){
tree.assign(n<<2,decltype(tree)::value_type());
}
void add(int l,int r,int p,int L,int R,array<int,2>tim){
if(L>r||R<l)return;
if(L<=l&&r<=R){
tree[p].emplace_back(tim);
return;
}
int mid=l+r>>1;
add(l,mid,p<<1,L,R,tim);
add(mid+1,r,p<<1|1,L,R,tim);
}
};
class DSU{
vector<int>f;
vector<int>d;
stack<tuple<int,int,int>>stk;
public:
DSU(int _n){
f.resize(_n+3);
d.resize(_n+3);
iota(f.begin(),f.end(),0);
fill(d.begin(),d.end(),1);
}
int find(int x){
return f[x]==x?x:find(f[x]);
}
bool unite(int x,int y){
x=find(x),y=find(y);
if(x==y)return false;
if(d[x]>d[y])swap(x,y);
f[x]=y;
stk.push({x,y,d[y]});
d[y]=max(d[y],d[x]+1);
return true;
}
void erase(){
auto[x,y,D]=stk.top();
stk.pop();
f[x]=x;
d[y]=D;
}
};
map<array<int,2>,int>mp;
void solve(Segtree&sgt,DSU&dsu,vector<string>&now,int l,int r,int p,bool k=false){
if(l==r){
int cnt=0;
debug(l);
debug(r);
for(auto[x,y]:sgt.tree[p]){
cnt+=dsu.unite(x,y+n);
cnt+=dsu.unite(x+n,y);
k|=(dsu.find(x)==dsu.find(x+n));
k|=(dsu.find(y)==dsu.find(y+n));
debug(x);
debug(dsu.find(x)==dsu.find(x+n));
debug(y);
debug(dsu.find(y)==dsu.find(y+n));
}
now.push_back(k?"No":"Yes");
while(cnt--)dsu.erase();
return;
}
int cnt=0;
debug(l);
debug(r);
for(auto[x,y]:sgt.tree[p]){
cnt+=dsu.unite(x,y+n);
cnt+=dsu.unite(x+n,y);
k|=(dsu.find(x)==dsu.find(x+n));
k|=(dsu.find(y)==dsu.find(y+n));
debug(x);
debug(dsu.find(x)==dsu.find(x+n));
debug(y);
debug(dsu.find(y)==dsu.find(y+n));
}
debug(endl);
int mid=l+r>>1;
solve(sgt,dsu,now,l,mid,p<<1,k);
solve(sgt,dsu,now,mid+1,r,p<<1|1,k);
while(cnt--)dsu.erase();
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin>>n>>m>>k;
DSU dsu(n<<1);
Segtree sgt(k);
for(int i=1;i<=m;i++){
int x,y,l,r;
cin>>x>>y>>l>>r;
++l;
if(x>y)swap(x,y);
sgt.add(1,k,1,l,r,{x,y});
}
vector<string>ans;
solve(sgt,dsu,ans,1,k,1);
for(auto i:ans)cout<<i<<"\n";
return 0;
}
```
:::
写作不易、在期末前更新也不易,本篇文章共 $1532$ 行、$30109$ 个字符,如果这篇文章对你有帮助的话,麻烦点个小小的赞,谢谢!