题解 P8934【[JRKSJ R7] TSM eerT】
cyffff
·
·
题解
\text{Link}
题意
对于一个 n 个结点的带边权的树 T,定义 \text{dis}(x,y) 为 T 中 x\to y 路径上的边权和。再定义一个 n 个结点的无向完全图 p(T)=G,其中 \forall x,y\in [1,n],G 中边 (x,y) 的边权为 \text{dis}(x,y)。
定义 f(T) 为 p(T) 的最大生成树。特别的,若 p(T) 的最大生成树不唯一,请立刻判断出并报告。
给定树 T_0 和整数 k,求 f^k(T_0)。边权为正整数。
若 \exists x\in[0,k-1] 使得 p(f^x(T_0)) 的最大生成树不唯一,输出 -1。否则,输出 f^k(T_0) 的所有边权和对 2^{32} 取模的结果。
## 思路
来补个严谨证明。
考虑 $k=1$ 的部分分。
使用 $\operatorname{Boruvka}$ 算法。我们对每个点找到距离它最远的点并与其连边。很显然,经过一次 $\operatorname{Boruvka}$ 算法,所有的点已经连通。原因是树上每个点距离最远的点为直径两端点之一,而直径两端点互相连接。
假设答案不是 $-1$,我们就已经得到了 $f(T_0)$ 了。来判断答案是不是 $-1$,共有以下情况:
- 直径不唯一
我们先证明,不会存在两条互不相交的直径。
反证,考虑存在下面的树,满足 $3\to 4$,$6\to 7$ 为两条直径。
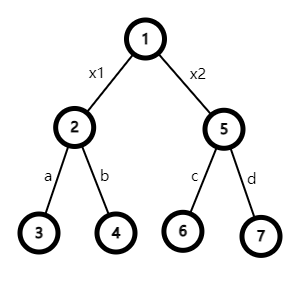
不妨令 $x=x_1+x_2>0$,$a>b>0$,$c\ge d>0$。
显然,$a+b\ge a+x+c$,$c+d\ge a+x+c$,所以 $b\ge c+x$,$d\ge a+x$。所以 $b>c\ge d>a$,矛盾。当 $a=b$ 时也易证矛盾。
所以,树不存在两条互不相交的直径。我们还可以证明如果有多条直径,则对于每一条直径,必然有一条其他直径与它在一个端点相交。
于是我们可以找出一条直径 $x\to y$,算出所有的 $\operatorname{dis}(i,x)$ 和 $\operatorname{dis}(i,y)$,如果有 $\operatorname{dis}(i,x)=\operatorname{dis}(x,y)$ 或 $\operatorname{dis}(i,y)=\text{dis}(x,y)$($i\ne x,i\ne y$)则直径不唯一。
直径不唯一时答案也不一定为 $-1$。当所有直径有同一个端点(具体为上述两种情况仅满足一个),设为 $x$,并且所有点到 $x$ 距离都大于到另一个端点的距离,并且 $k=1$ 的时候,答案不为 $-1$,其余情况都为 $-1$。
考虑找出一条直径,枚举转折点 $i$,找出 $i$ 子树内 $dis(i,k)$ 最大的两个 $k$,则直径为 $\max(\text{dis}(i,k_1)+\text{dis}(i,k_2))$,树形 $\text{dp}$ 即可。
- 直径唯一
则此类情况下,答案为 $-1$ 当且仅当有一个点 $i$ 到直径两端距离相等。
接下来考虑 $k>1$ 的情况。
依然考虑以上算法,考虑一次操作后树为两个点分别挂着一堆点(分别将两个点集记为 $S_x,S_y$)。令 $S_x$ 中与 $x$ 相连边最长的点为 $m_x$,$m_y$ 同理。考虑由于 $x\to y$ 的边权为此时树中的最大边权,此时树的直径为 $m_x\to m_y$,则 $S_x$ 中的点经历这次操作都会连到 $m_y$,且边权为原来的加上 $v_{x\to y}+v_{y\to m_y}$,$S_y$ 中的点同理。新树中 $v_{m_x\to m_y}$ 等于旧树中 $v_{x\to y}+v_{x\to m_x}+v_{y\to m_y}$。
考虑边权的增长是指数级的,我们不能直接维护,必须在模 $2^{32}$ 意义下维护相对顺序。考虑拿两个队列 $q_1,q_2$ 维护 $S_x,S_y$ 中 $v_{x\to p}$ 的相对顺序。考虑一次操作后先得出 $q_1,q_2$ 并进行排序。考虑一次操作,我们会取出两边的最大值并将其置为零,将其余的整体加上一个正数,并将 $x$ 加入队列。考虑维护整体加的 $tag$,由于 $x$ 原先是最小值 $0$,我们将 $-tag$ 加入最后即可。
再考虑判 $-1$:
- 直径不唯一
即 $S_x$ 或 $S_y$ 中前两大值相等。不能直接判断,因为我们的边权是在模 $2^{32}$ 下考虑的。但是我们考虑一次操作后只会取 $k-1$ 次,我们只需要在一次操作后的 $S_x$ 和 $S_y$ 中判断 $i\in[1,\min(n,k-1)]$ 中是否 $q_{o,i}=q_{o,i+1}$ 即可,需要注意,当 $S_x$ 与 $S_y$ 有一个空的时候不应判断这种情况,因为此时直径不唯一但有同一端点。
或者你加个哈希也可以。
这个情况是答案必然为 $-1$ 的。
- 直径唯一
不可能有任何一个点到新直径两端距离相等,因为旧直径是旧的树中边权最大的。
综上,我们做到了 $O(n\log n+k)$ 的复杂度。瓶颈是排序。
代码细节比较多,就贴上来了:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ui unsigned
namespace IO{//by cyffff
}
const int N=1e6+10;
int n,k,head[N],cnt;
struct Edge{
int to,nxt,w;
}a[N<<1];
inline void add(int u,int v,int w){
cnt++;
a[cnt].to=v;
a[cnt].nxt=head[u];
a[cnt].w=w;
head[u]=cnt;
}
int s,t;
ll mx,dep[N][2],dis;
inline void dfs(int x,int fa,int tp){
if(!fa) dep[x][tp]=0;
for(int i=head[x];i;i=a[i].nxt){
int t=a[i].to;
if(t==fa) continue;
dep[t][tp]=dep[x][tp]+a[i].w;
dfs(t,x,tp);
}
}
vector<ll>s1,s2;
queue<ui>d1,d2;
ui tag1,tag2,di,ans;
/*
7 1
1 1
2 2
1 4
2 4
4 4
5 4
*/
int main(){
// freopen("16.in","r",stdin);
n=read(),k=read();
for(int i=2;i<=n;i++){
int f=i-read(),w=read();
add(f,i,w),add(i,f,w);
}
dfs(1,0,0);
for(int i=1;i<=n;i++)
if(dep[i][0]>mx) mx=dep[i][0],s=i;
dfs(s,0,0);
for(int i=1;i<=n;i++)
if(dep[i][0]>dis) dis=dep[i][0],t=i;
dfs(t,0,1);
bool fl1=0,fl2=0;
for(int i=1;i<=n;i++){
if(i==s||i==t) continue;
if(dep[i][0]==dep[t][0]) fl1=1;
if(dep[i][1]==dep[s][1]) fl2=1;
}
if(fl1&&fl2) return puts("-1"),0;
if((fl1||fl2)&&k>1) return puts("-1"),0;
if(fl1){
for(int i=1;i<=n;i++){
if(i==s||i==t) continue;
if(dep[i][0]<dep[i][1]) return puts("-1"),0;
}
}
if(fl2){
for(int i=1;i<=n;i++){
if(i==s||i==t) continue;
if(dep[i][0]>dep[i][1]) return puts("-1"),0;
}
}
for(int i=1;i<=n;i++){
if(i==s||i==t) continue;
if(dep[i][0]==dep[i][1]) return puts("-1"),0;
if(dep[i][0]>dep[i][1]) s1.push_back(dep[i][0]);
else s2.push_back(dep[i][1]);
}
sort(s1.begin(),s1.end(),greater<ll>());
sort(s2.begin(),s2.end(),greater<ll>());
if(s1.size()&&s2.size()){
for(int i=0;i+1<s1.size()&&i<min(n,k-1);i++)
if(s1[i]==s1[i+1]) return puts("-1"),0;
for(int i=0;i+1<s2.size()&&i<min(n,k-1);i++)
if(s2[i]==s2[i+1]) return puts("-1"),0;
}
for(auto x:s1) d1.push((ui)x);//,printf("%d ",x);puts("");
for(auto x:s2) d2.push((ui)x);//,printf("%d ",x);puts("");
di=dis;
for(int i=2;i<=k;i++){
ui x=0,y=0;
bool fl1=0,fl2=0;
if(!d1.empty()) x=d1.front()+tag1,d1.pop(),fl1=1;
if(!d2.empty()) y=d2.front()+tag2,d2.pop(),fl2=1;
if(fl1) d1.push(-tag1),tag1+=y+di;
if(fl2) d2.push(-tag2),tag2+=x+di;
di+=x+y;
// printf("%d %d %d %d %d\n",x,y,tag1,tag2,di);
}
while(!d1.empty()) ans+=d1.front()+tag1,d1.pop();
while(!d2.empty()) ans+=d2.front()+tag2,d2.pop();
ans+=di;
write(ans);
flush();
}
```