单调栈与计数1
ql12345
·
·
题解
二维前缀和+单调栈
很不错的一道题,看完代码就感觉很简单了(思路自己想不好想),也理解思路了,但光自己想和看文字题解会很抽象
大体思路:
作为计数问题,又是二维的平面,肯定先想到枚举点作为矩形顶点,用某种方法统计所有矩形,加上简单容斥,使答案不重不漏
具体思路:
说明:本文内有关横纵两个方向叠加的描述的定义都参照初中学的平面直角坐标系(描述对象为原点)
-
对每个点:分别求出以该点为(右上,左上,左下,右下)端点的矩形数量
-
对每个点:将以“该点为右下端点的矩形数”与“不在该点左上方(包含坐标轴)的矩形数”的乘积加入答案
-
去掉一些重复计数部分(后面会讲)
Part 1(本题的重点):
说明:只会以“以该点为右下端点的矩形数量”为例进行讲解
先来看一道单调栈的经典题(请认真看):最大矩形面积
该题简略做法:
将每个高度(不同位置独立计算)与能达到的最大宽度形成的矩形计入答案
通过单调栈维护单调上升的子矩形做到这一点:
核心Code:(记住这个写法)
ans=top=0;
for(int i=1;i<=n+1;++i){
if(i<=n) read(a[i]);
else a[i+1]=0;
if(a[i]>stk[top])
stk[++top]=a[i],wid[top]=1;
else{
int width=0;
while(stk[top]>a[i]){
width+=wid[top],
ans=max(ans,width*stk[top]);
top--;
}
stk[++top]=a[i],
wid[top]=width+1;
}
}
再挂一道经典题,做过的回忆,没做过的就自动忽略:笛卡尔树+树形dp
在做这题的时候,其实给我印象最深的是:先考虑如果是一个矩形怎么做,然后将原图划分为若干矩形,将答案累加
回归本题:
我们统计以该点为右下角的矩形数,就是统计合法的左上角数
如果该点左上方有一个矩形,它对矩形数的贡献显然就是矩形点数(我们规定了矩形的右下端点,矩形内所有点都可以是左上端点)
将问题分为两个部分:
-
找出矩形
-
将矩形答案累加,不重不漏
先找出矩形:
绿色点为当前点,它左上方的相连的黑色格点构成了一列一列连续的矩形(与《最大矩形面积》的原图一样)
将矩形答案累加就非常简单了:
于是我们就可以在原来代码的基础上改为:“每次更新ans 改为 减去top元素高出部分对答案造成的贡献,并加上每个位置记录答案的语句”
解释(这里有一个优化):
因为每次对每个位置的点计算答案复杂度高(大量重复计算),这里改为“前面计算的是一个阶梯的前缀和的贡献”,高出部分没有贡献但被统计到了,弹栈的时候减去,同时因为后面的所有点都是由当前统计的点的答案初始化的,所以这里弹栈一次即可,复杂度线性
可能还是有一点抽象,看一下代码:
行后有斜线的是《最大矩形面积》代码有改动的地方
for(int i=1;i<=n;++i){
top=0;
for(int j=1;j<=n;++j){
if(u[i][j]>stk[top])
stk[++top]=u[i][j],wid[top]=1,
dir[2][i][j]=dir[2][i][j-1]+u[i][j];//
else{
LL width=0;
LL now=dir[2][i][j-1]+u[i][j];//
while(stk[top]>u[i][j]){
width+=wid[top];
now=(now-wid[top]*(stk[top]-u[i][j])+p)%p;//
top--;
}
stk[++top]=u[i][j],
wid[top]=width+1,
dir[2][i][j]=now;//
}
}
}
Part 1完结~
Part 2:
本题记答案具体方法很有特点(我是第一次见,觉得这个地方很不好想到)
先上图:
这个绿色部分的矩形数显然可以通过对“以该点为左上端点的矩形数量”的数组求二维前缀和后,再加上容斥$O(1)$查询
正确性证明:
对于一个矩形,它的右下端点唯一,对不在当前点左上方的矩形,可以在当前点计算它们的贡献,对于在当前点左上方的矩形,在枚举到这个矩形的右下端点的时候已经对矩形对计算过一次贡献,所以一个矩形对不会被漏掉
Part 2完结~,让我们带着另一半证明到Part 3
### Part 3:
但一个矩形对是可能会被重复计算的,首先明确:一个矩形对只会在其中一个矩形被枚举到时被算入答案,所以最多会被算两次(多算1次)
结合图不难发现:一个矩形对被计算两次当且仅当它满足以下情形:
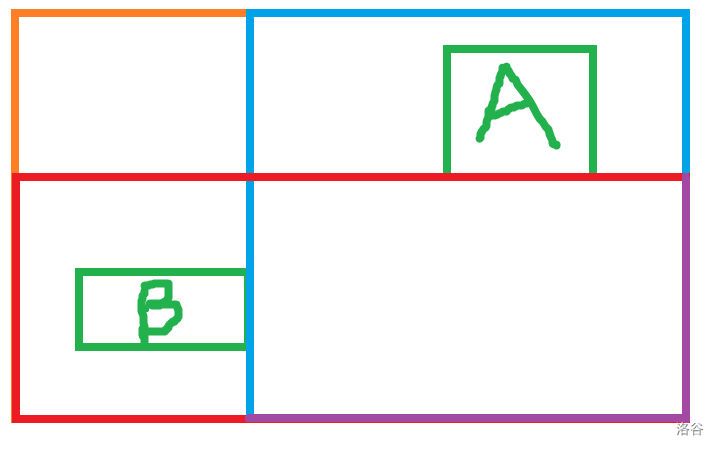
(矩形A会在蓝色矩形中被计算,矩形B会在红色矩形中被计算)
去重:
枚举上方的矩形左下端点,右上端点在该点左下方的矩形数量乘上以该点为左下端点的矩形数量即为该点需要减去的贡献
因为重复计算的一对矩形对只会在上方的矩形处被去重,所以不会重复去重,就做到不重不漏
### 实现:
注意字符串的读入,可以参考我的读入,输入数据每行后有空格(读入错卡了我好久)
题中说了,只有一个点的矩形不算矩形,所以代码中部分地方读者可以看到$-1$,没有$-1$的地方一般是之前计算的时候减去1了
代码中$dir[]$是direction(方向)的意思,$1/2/3/4$分别对应平面直角坐标系中的四个象限相对原点所在的方位
代码中部分长式子经过了换行处理
### 提醒:
写代码之前做好要调很久的心理准备(我调了4个小时)
另外,前面再写Part 1部分的时候,千万千万考虑清横纵坐标的$+1,-1$以及到底应该是哪一个数组($1/2/3/4$)
### Code:
```cpp
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1005,p=10007;
int n;
LL u[N][N],d[N][N];
LL stk[N],wid[N],top;
LL dir[5][N][N];
char mp[N][N];
void init(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%s",&mp[i][1]);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
u[i][j]=(mp[i][j]=='B')?u[i-1][j]+1:0;
for(int i=n;i>=1;--i)
for(int j=1;j<=n;++j)
d[i][j]=(mp[i][j]=='B')?d[i+1][j]+1:0;
}
void get_dir(){
for(int i=1;i<=n;++i){
top=0;
for(int j=n;j>=1;--j){
if(u[i][j]>stk[top])
stk[++top]=u[i][j],wid[top]=1,
dir[1][i][j]=dir[1][i][j+1]+u[i][j];
else{
LL width=0;
LL now=dir[1][i][j+1]+u[i][j];
while(stk[top]>u[i][j]){
width+=wid[top];
now-=wid[top]*(stk[top]-u[i][j]);
top--;
}
stk[++top]=u[i][j],
wid[top]=width+1,
dir[1][i][j]=now;
}
}
}
for(int i=1;i<=n;++i){
top=0;
for(int j=1;j<=n;++j){
if(u[i][j]>stk[top])
stk[++top]=u[i][j],wid[top]=1,
dir[2][i][j]=dir[2][i][j-1]+u[i][j];
else{
LL width=0;
LL now=dir[2][i][j-1]+u[i][j];
while(stk[top]>u[i][j]){
width+=wid[top];
now=(now-wid[top]*(stk[top]-u[i][j])+p)%p;
top--;
}
stk[++top]=u[i][j],
wid[top]=width+1,
dir[2][i][j]=now;
}
}
}
for(int i=n;i>=1;--i){
top=0;
for(int j=1;j<=n;++j){
if(d[i][j]>stk[top])
stk[++top]=d[i][j],wid[top]=1,
dir[3][i][j]=dir[3][i][j-1]+d[i][j];
else{
LL width=0;
LL now=dir[3][i][j-1]+d[i][j];
while(stk[top]>d[i][j]){
width+=wid[top];
now=(now-wid[top]*(stk[top]-d[i][j])+p)%p;
top--;
}
stk[++top]=d[i][j],
wid[top]=width+1,
dir[3][i][j]=now;
}
}
}
for(int i=n;i>=1;--i){
top=0;
for(int j=n;j>=1;--j){
if(d[i][j]>stk[top])
stk[++top]=d[i][j],wid[top]=1,
dir[4][i][j]=dir[4][i][j+1]+d[i][j];
else{
LL width=0;
LL now=dir[4][i][j+1]+d[i][j];
while(stk[top]>d[i][j]){
width+=wid[top];
now=(now-wid[top]*(stk[top]-d[i][j])+p)%p;
top--;
}
stk[++top]=d[i][j],
wid[top]=width+1,
dir[4][i][j]=now;
}
}
}
}
void calc(){
for(int i=n;i>=1;--i)
for(int j=n;j>=1;--j)
dir[4][i][j]=dir[4][i][j]>0?
dir[4][i][j]-1LL+dir[4][i+1][j]+dir[4][i][j+1]-dir[4][i+1][j+1]
:(dir[4][i+1][j]+dir[4][i][j+1]-dir[4][i+1][j+1]);
for(int i=n;i>=1;--i)
for(int j=1;j<=n;++j)
dir[3][i][j]=dir[3][i][j]>0?
dir[3][i][j]-1LL+dir[3][i+1][j]+dir[3][i][j-1]-dir[3][i+1][j-1]
:(dir[3][i+1][j]+dir[3][i][j-1]-dir[3][i+1][j-1]);
LL ans=0;
for(int i=1;i<=n;++i)//统计答案
for(int j=1;j<=n;++j)
ans=dir[2][i][j]>0?
ans+(dir[2][i][j]-1LL)*(dir[4][1][j+1]+dir[4][i+1][1]-dir[4][i+1][j+1])
:ans;
for(int i=1;i<=n;++i)//去重
for(int j=1;j<=n;++j)
ans=dir[1][i][j]>0?
ans-(dir[1][i][j]-1LL)*(dir[3][i+1][j-1])
:ans;
printf("%lld",ans%p);
}
signed main(){
init();
get_dir();
calc();
return 0;
}
```