快速傅里叶变换(FFT)学习笔记
KobeBeanBryantCox
·
·
算法·理论
快速傅里叶变换(FFT)学习笔记
前言
这是我第二篇学习笔记,上一篇 SAM 的在这里。
我一般不写学习笔记,除非太难理解或者算法本身太过巧妙。
不同于 SAM,这次写学习笔记的原因是因为其太过巧妙了。
前置知识:矩阵,弧度制,三角函数,代数基础,函数基础,复数概念。
参考资料:这里。本学习笔记详细了视频的内容,然后那个视频还是有错误的,我将在这里指正其错误。
如果任何一句话您看不懂,请先尝试找 DeepSeek,它很聪明。如果再看不懂,请评论或者私信我。
01. 引入
如果我们有两个多项式 A(x)=x^2+3x+2 和 B(x)=2x^2+1。
我们要把他相乘得到 C(x)=A(x)B(x),我们平时是怎么做的?
在数学上,我们使用乘法分配律,如下:
C(x) & =(x^2+3x+2)(2x^2+1) \\
& =x^2(2x^2+1)+3x(2x^2+1)+2(2x^2+1) \\
& =2x^4+x^2+6x^3+3x+4x^2+2 \\
& =2x^4+6x^3+5x^2+3x+2
\end{aligned}
这是数学上的做法。
在计算机中,首先一个重要的事情是,我们如何存储这个多项式?
最自然的做法是用数组存储多项式的系数,如下:
$B(x)=1+2x^2\Rightarrow B=[1,0,2]$。
$C(x)=2+3x+5x^2+6x^3+2x^4\Rightarrow C=[2,3,5,6,2]$。
注意,指数从低到高,因为这样的话,数组的第 $k$ 项正好对应多项式的 $k$ 次项系数(数组从 $0$ 开始)。
我们称这种做法是多项式的**系数表示法**。
一般地,给定两个 $d$ 次多项式,相乘后会得到 $2d$ 次多项式。
所以我们会枚举,然后一一配对,系数相乘指数相加,贡献到对应位置。
这样做是 $O(d^2)$ 的,因为我们 $A$ 的每一项都要与 $B$ 的每一项相乘。
我们能优化吗?
有请 FFT(Fast Fourier Transform,快速傅里叶变换)!
---------------------
# 02. 快速傅里叶变换
## 多项式的值表示法
从最简单开始看。一个一次多项式 $f(x)=kx+b$。
这是不是我们小学二年级学过的一次函数(直线)啊?
根据学前班的知识,两点确定一条直线。
所以我们随便取两个不同的点 $x_0,x_1$,这条 $f(x)=kx+b$ 可以被我们表示成 $[(x_0,f(x_0)),(x_1,f(x_1))]$。
同样的,二次多项式能用 $3$ 个点表示;$d$ 次多项式能用 $d+1$ 个点表示。
简单证明一下:
> 考虑一个多项式 $p(x)=a_0+a_1x+a_2x^2+\cdots+a_dx^d$。
>
> 现在我们需要表示出 $a_0,a_1,\cdots,a_d$ 一共 $d+1$ 个数字。
>
> 我们扔 $d+1$ 个不相同的点进去,能形成 $d+1$ 个方程。
>
> $d+1$ 个未知数 $d+1$ 个方程,我们是不是能唯一确定未知数的值啊?
>
> 证毕。
我们称用点表示多项式的方法,叫做多项式的**值表示法**。
这样表示,我们多项式相乘就方便了很多。为什么呢?
举个例。我们把 $A(x)=x^2+2x+1$ 和 $B(x)=x^2-2x+1$ 的图像画出来:
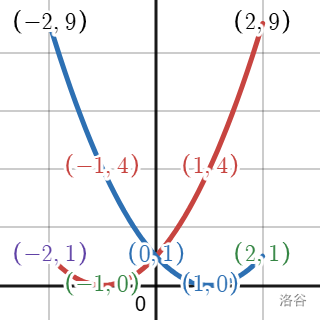
红色的是 $A$,蓝色的是 $B$。
我们用 $x=-2,-1,0,1,2$ 表示 $A=[(-2,1),(-1,0),(0,1),(1,4),(2,9)]$ 和 $B=[(-2,9),(-1,4),(0,1),(1,0),(2,1)]$。
为什么要选取 $5$ 个 $x$ 呢?因为 $A$ 和 $B$ 都是二次多项式,相乘后是 $4$ 次多项式,要用 $5$ 个点表示。
然后用幼儿园学到的竖式计算:
$$\begin{array}{lr}
&[(-2,1),(-1,0),(0,1),(1,4),(2,9)]\\
&\times[(-2,9),(-1,4),(0,1),(1,0),(2,1)]\\
&\overline{[(-2,9),(-1,0),(0,1),(1,0),(2,9)]}
\end{array}$$
原理很简单,$C(-2)=A(-2)\times B(-2)=1\times 9=9$,以此类推。
这样我们就得到了 $C=[(-2,9),(-1,0),(0,1),(1,0),(2,9)]$。
把这几个点描在图像上:
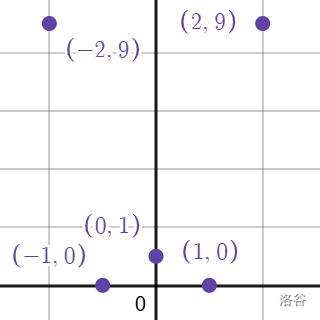
这几个点唯一确定一个四次函数 $C(x)=x^4-2x^2+1$(先不用管是怎么算出来表达式的):
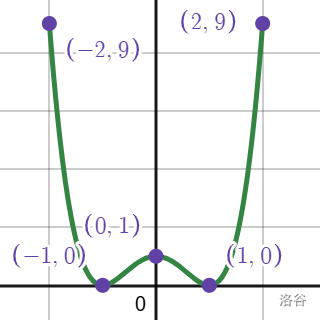
好了,现在我们已经把乘法从 $O(d^2)$ 优化成了 $O(d)$。
现在问题是:怎么把系数表达式转化成值表达式,又怎么把值表达式转回系数表达式。
-------------------
## 求值
其实求值就是**从系数表示转成值表示**的过程。
想想最暴力的方法是什么。是不是随便取 $d+1$ 个点然后算函数值?
但是这样还是 $O(d^2)$ 的,因为我们每一个点要用 $O(d)$ 时间算值,又有 $d+1$ 个点。
试着简化问题,若有一个 $f(x)=x^2$,我们要取 $n=8$ 个点($n$ 理论上是可以随便决定的,只需要满足 $n\ge d+1$)。
-------------------
### 奇偶函数
由于我们想减少计算量,考虑这样的一对点:我们知道了其中一个的值,就能立刻知道另一个。
这些点可以是这样的:
$$\fbox{$\begin{array}{}(1,1),(-1,1)\\(2,4),(-2,4)\\\cdots\\(4,16),(-4,16)\end{array}$}$$
我们只需要取相反数的点对即可。
这其中的原理很简单,$f$ 是一个偶函数(即 $f(x)=f(-x)$)。
如果三次函数呢?
$$\fbox{$\begin{array}{}(1,1),(-1,-1)\\(2,8),(-2,-8)\\\cdots\\(4,64),(-4,-64)\end{array}$}$$
这也是可以的,只需要加一个负号。
原理也很简单,三次函数是奇函数(即 $-f(x)=f(-x)$)。
同样的四次函数五次函数都是这样。
这样就只用算一半的点了!~~虽然还是没什么用但是先别急。~~
----------------
### 非奇非偶函数
看看上面的是否对所有多项式都有用。
随便举个例子:$f(x)=3x^5+2x^4+x^3+7x^2+5x+1$。
然后根据上面的规律,我们**奇偶分开**:
$$\begin{aligned}f(x)&=(2x^4+7x^2+1)+(3x^5+x^3+5x)\\&=(2x^4+7x^2+1)+x(3x^4+x^2+5)\\&=f_e(x^2)+x\times f_o(x^2)\end{aligned}$$
在这里,我们定义 $f_e(x^2)=2x^4+7x^2+1$ 和 $f_o(x^2)=3x^4+x^2+5$。
注意不是 $f_e(x)$ 和 $f_o(x)$,而是 $f_e(x^2)$ 和 $f_o(x^2)$。可以用 $x^2$ 是因为这个多项式都是偶数次项。
所以我们得到了如下规律:
$$\fbox{$\begin{array}{l}f(x_i)&=f_e(x_i^2)+x_i\times f_o(x_i^2)\\f(-x_i)&=f_e(x_i^2)-x_i\times f_o(x_i^2)\end{array}$}$$
所以假如我们知道了 $f_e(x_i^2)$ 和 $f_o(x_i^2)$,我们能一次性算 $f(x_i)$ 和 $f(-x_i)$。
这个时候我们令 $t=x_i^2$,那么 $f_e(x_i^2)=f_e(t)=2t^2+7t+1$,$f_o(x_i^2)=f_o(t)=3t^2+t+5$。
所以我们需要计算 $f_e(t)$ 和 $f_o(t)$ 来得到 $f(x)$。
你会发现我们把求 $f(x)$ 这个 $d$ 次多项式转化成求 $f_e(t)$ 和 $f_o(t)$ 这两个 $\lfloor\dfrac d 2\rfloor$ 次多项式(当 $d$ 为偶数时貌似是一个 $\dfrac d 2$ 和一个 $\dfrac d 2-1$ 的,不过这不重要)。
这是子问题啊,不断**递归解决**即可!
~~但是这样会有亿点小问题,待会就说。~~
这样做居然是 $O(n\log n)$ 的!因为递归只有 $\log n$ 层,每一层要处理 $O(n)$ 的信息。
我们将会得到 $f=[(x_1,f(x_1)),(-x_1,f(-x_1)),\cdots,(x_{\frac n 2},f(x_{\frac n 2})),(-x_{\frac n 2},f(-x_{\frac n 2}))]$。
-------------------------
### 寻找合适的数
你们注意到这里有一个小问题没有?
我们递归解决的是 $f_e(t),f_o(t)$,假设可以随便取 $t=[t_1,t_2,\cdots,t_{\frac n 2}]$,那么我们最终会得到 $f(x)$,其中 $x=[\pm\sqrt{t_1},\cdots,\pm\sqrt{t_{\frac n 2}}]$。
虽然 $f$ 是符合我们的预期的(拥有成对相反数),但是由于有 $\sqrt t$,所以 $t\ge 0$,这说明我们不能递归解决 $f_e$ 和 $f_o$ 了。
(因为递归的目的是要用相反数来减少计算,而所有 $\{t_i|i\in[1,\dfrac n 2]\}$ 都是非负数,不存在相反数,所以递归不下去了。)
举个例子,如果递归初始使用 $x=[1,-1,2,-2]$,进入第二层递归时 $t=[1,4]$,此时 $t$ 的两个值不是相反数,不能算出一个立即得出另一个,也就是说,这里就不能递归了。
好了,FFT 最天才的想法来了!
我们**强制让 $t$ 有一半是负数,另一半是正数**。
由于 $x=[\pm\sqrt{t_1},\cdots,\pm\sqrt{t_{\frac n 2}}]$,也就是说**有一半的 $x$ 是复数**~~(别看到复数就跑了,待会有详细解释)~~!
我们还要专门挑一些复数,使得它们平方之后,依旧是**正负成对**出现的。
怎么挑呢?举个例子吧。
$f(x)=x^3+x^2-x-1$。
这是一个三次多项式,我们需要 $4$ 个点来表示它。
这 $4$ 个点要正负成对出现,我们不妨设其为 $[x_1,-x_1,x_2,-x_2]$,这是递归的第一层。
递归后第二层要解决 $[x_1^2,x_2^2]$ 的子问题。
现在我们知道 $x_1^2$ 和 $x_2^2$ 也要是一对相反数。所以 $x_2^2=-x_1^2$。
再递归下去第三层只有一个点了 $x_1^4$。
现在我们可以随便取这个点,我们不妨就令 $x_1^4=1$ 吧。
那么第三层 $[1]$,第二层 $[1,-1]$,第一层 $[1,-1,x_2,-x_2]$。
**这个 $x_2$ 等于 $\sqrt{x_2^2}=\sqrt{-x_1^2}=\sqrt{-1}=i$,对吧!!!**
所以第一层是 $[1,-1,i,-i]$。
> ### 【补充】复数概念
>
> 1. 虚数
>
> 我们定义 $i=\sqrt{-1}$,$i$ 是虚数单位。你不用管这个 $i$ 的具体含义,它就是个符号。
>
> 2. 复数
>
> 一个复数 $z$,在复平面能表示成 $z=a+bi$,这里的 $i$ 是单位不是常量,不要理解成 $b\times i$。
>
> 其中这里的 $a$ 是实数,叫做 $z$ 的实部;$bi$ 是虚数,叫做 $z$ 的虚部。
>
> 事实上 $z$ 在复平面是能表示出来的。我们令 $x$ 轴为实轴(单位长度为 $1$),$y$ 轴为虚轴(单位长度为 $i$)。
>
> **$z=a+bi$ 其实是复平面上坐标为 $(a,bi)$ 的点。**因为这里的加法事实上是向量的加法。
>
> 不过你不理解向量也无所谓,你只需要记住 **$z=a+bi$ 对应在 $(a,bi)$** 即可。
>
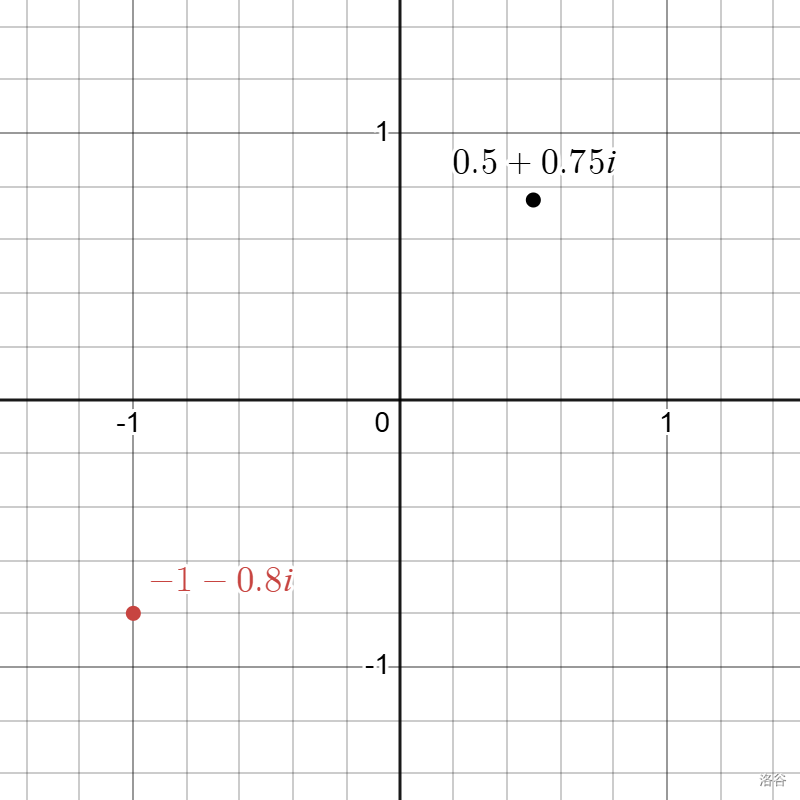
> 下图描述了 $z=0.5+0.75i$ 和 $z=-1-0.8i$ 的位置。
>
> 
从另一个视角来看:
我们实际上是解了一个方程 $x^4=1$,得到了解 $[1,-1,i,-i]$,我们把这四个解称为 **$1$ 的四个四次方根**。
现在来推广到 $d$ 阶多项式。按理来讲我们是需要取 $d+1$ 个点。
但是由于我们每次要折半,不妨让 $n$ 是 $>d$ 的第一个 $2$ 的整数次幂,这不影响答案的计算。
所以我们选的点就是 **$1$ 的 $n$ 个 $n$ 次方根**(即,解 $z^n=1$ 得到的 $n$ 个 $z$。)
但是你们不想想它为什么是对的吗?你不考虑怎么解出这些解吗?
----------------------
### 证明以及求解这些数
具体的,我们需要证明为什么这些数正负成对出现,并且平方后依然正负成对出现,再平方后还是这样。
> ### 【引入】单位圆
>
> 给出结论:**$1$ 的 $n$ 次方根可以被解释为复平面上沿着单位圆等距排布的 $n$ 个点**。
>
> 不理解就对了。下面来解释。
>
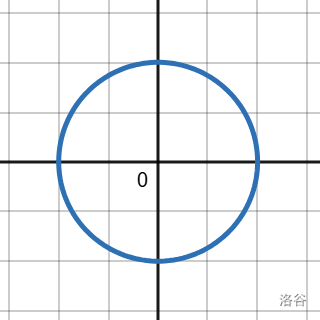
> 下图是单位圆(很好理解啊,半径是一个单位的圆嘛):
>
> 
>
> 这个圆与 $x$ 轴(实轴)交点为 $1,-1$,与 $y$ 轴(虚轴)交点为 $i,-i$($i$ 是虚数单位,只是一个单位而已)(上图交点数字未标出)。
>
> 因为我们知道,复数 $z=a+bi$ 画在复平面上是 $(a,bi)$(上文提到过)。
>
> 我们定义 $r$ 为向量 $z$ 的模长(即 $(a,bi)$ 到原点的距离),有 $r=\sqrt{a^2+b^2}$。
>
> 我们定义 $\theta$ 为辐角。这是向量 $z$ 与正实轴($x$ 轴正半轴)的逆时针旋转的夹角。
>
> - $\cos\theta=\dfrac{\text{邻边}}{\text{斜边}}=\dfrac a r\Rightarrow a=r\cos\theta
-
\sin\theta=\dfrac{\text{对边}}{\text{斜边}}=\dfrac b r\Rightarrow b=r\sin\theta
- 所以 z=a+bi=r\cos\theta+i\cdot r\sin\theta=r(\cos\theta+i\sin\theta)。
因为有欧拉公式:e^{i\theta}=\cos\theta+i\sin\theta,我们可以得到 z=re^{i\theta}。
所以 z^n=r^ne^{in\theta}。
现在来解 z^n=1。
因为 1=1\cdot e^{i\cdot0},所以 z^n=1\cdot e^{i\cdot 0}=r^ne^{in\theta}。
为了使其相等,我们要满足两个条件:
- 模相等:r^n=1;
- 辐角相差 2\pi 的倍数(弧度制下 2\pi 是 360 度,转了一圈):n\theta=0+2\pi k,k\in\mathbb{Z}。
解得:
- 模 r=1;
- 辐角 \theta=\dfrac{2\pi k}n。
由于 r=1,所以它们都在单位圆上。
根据解得的 \theta,相邻两个辐角差为 \dfrac{2\pi(k+1)}n-\dfrac{2\pi k}n=\dfrac{2\pi}n。
直观理解就是把 2\pi 的圆周均匀分成了 n 份,所以其等距分布。
我们这就证明了刚开始得出的结论。
此时 z=re^{i\theta}=1\cdot e^{i\cdot\frac{2\pi k}n},这就是 z^n=1 的解了,其中 k\in[0,n-1]。
我们定义 \omega_n=e^{\frac{2\pi i}n},我们称这个 \omega_n 叫做单位根。
不难发现 [\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}] 就是 1 的 n 个 n 次方根,因为代入它们后,会发现其与上文的 z=1\cdot e^{i\cdot\frac{2\pi k}n},k\in[0,n-1] 是相等的。
所以我们的 FFT 的第一层递归此时就是要在 1,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1} 处取点。
回到原来的问题,为什么这些 \omega_n^k 就能用来递归呢,具体的,为什么其一定有成对的相反数呢?
上图是 n=16 时的单位圆和单位根(上文强调过,n 只能取 2 的整数次幂)。
我们可以很清楚地看见 \omega_{16}^{j+\frac n 2}=-\omega_{16}^j(注意向量的复平面与平面直角坐标系的区别,复平面的负号是要求与原点对称),这个叫做单位根的对称性。
(其实根据这个还能推出单位根的周期性,不过不重要。)
上文说过,第 i 层递归用的数应该是第 i-1 层用的数的平方。
所以第二层用的数就是 [(\omega_{16}^0)^2,(\omega_{16}^1)^2,\cdots,(\omega_{16}^{7})^2](只取到 7 是因为 8\sim15 的点与 0\sim7 的点分别关于原点对称,平方后是同一个值。)
你会发现这些东西居然是 [\omega_{16}^0,\omega_{16}^2,\omega_{16}^4,\cdots,\omega_{16}^{12},\omega_{16}^{14}]。
然后它居然等价于 [\omega_8^0,\omega_8^1,\cdots\omega_8^7](可以画画图理解,会发现两者等价)。
(\omega_{2n}^{2k}=\omega_n^k 其实叫做折半引理,不过这也不重要。)
然后这些居然也是具有对称性的。再平方后也是同理的,直到只有一个值。
这样就选完数了。FFT 也就是这样了(是不是很简单),下面来对着代码总结 FFT 的过程。
FFT 递归版代码
别看我们说了这么多,其实代码超级短(12 行)!
我们一点一点来。
typedef double lf;
const lf PI=acos(-1);
void FFT(complex<lf>*a,int n)
{
}
这是定义 FFT 函数,表示将 a 这个系数表达式转化成值表达式,返回在 a 中。
complex 是 c++ STL 提供的复数模板。
传入的时候所有 a_k 的虚部都是 0i。
这里 n 是长度,传入的是大于应该有的次数的最小 2 的整数幂。
if(n==1)return;
长度为 1 直接退出。
int m=n>>1;
complex<lf>a0[m],a1[m];
for(int i=0;i<n;i+=2)a0[i>>1]=a[i],a1[i>>1]=a[i+1];
把其分成更小的长度 m,然后把 a 分为奇偶两部分。
FFT(a0,m),FFT(a1,m);
递归处理奇偶两部分。
complex<lf>wn={cos(2*PI/n),sin(2*PI/n)},w={1,0};
定义单位根 w_n。注意这里的 w 是单位根的幂次,会在循环中不断乘 w_n。
事实上,你使用:
complex<lf>wn=exp(complex<lf>{0,2*PI/n});
来定义单位根也是可以的(根据欧拉公式)。
但是很多题解用的都是第一种。我们就跟随潮流吧。(或许是因为精度的误差?但两种都能过模板题。有知道的麻烦告知我。)
for(int i=0;i<m;i++,w*=wn)a[i]=a0[i]+w*a1[i],a[i+m]=a0[i]-w*a1[i];
然后你把它们合起来就好了(根据先前计算的公式)。
为什么合起来的时候一定是前一半后一半呢?
先前的公式(去前文看):
\fbox{$\begin{array}{l}f(x_j)&=f_e(x_j^2)+x_j\times f_o(x_j^2)\\f(-x_j)&=f_e(x_j^2)-x_j\times f_o(x_j^2)\end{array}$}
我们知道此时 x_j=\omega^j,所以如下:
\fbox{$\begin{array}{l}f(\omega^j)&=f_e(\omega^{2j})+\omega^j\times f_o(\omega^{2j})\\f(-\omega^j)&=f_e(\omega^{2j})-\omega^j\times f_o(\omega^{2j})\end{array}$}
我们前文也说过 -\omega^j=\omega^{j+\frac n 2}=\omega^{j+m}(对称性),所以:
\fbox{$\begin{array}{l}f(\omega^j)&=f_e(\omega^{2j})+\omega^j\times f_o(\omega^{2j})\\f(\omega^{j+m})&=f_e(\omega^{2j})-\omega^j\times f_o(\omega^{2j})\end{array}$}
我们 f 的下标用的就是 \omega 的上标,所以一定是前一半后一半地存。
总代码如下:
typedef double lf;
const lf PI=acos(-1);
void FFT(complex<lf>*a,int n)
{
if(n==1)return;
int m=n>>1;
complex<lf>a0[m],a1[m]; // 这样开数组其实有点不太规范的
for(int i=0;i<n;i+=2)a0[i>>1]=a[i],a1[i>>1]=a[i+1];
FFT(a0,m),FFT(a1,m);
complex<lf>wn={cos(2*PI/n),sin(2*PI/n)},w={1,0};
for(int i=0;i<m;i++,w*=wn)a[i]=a0[i]+w*a1[i],a[i+m]=a0[i]-w*a1[i];
}
FFT 非递归代码
为了阅读的连续性,我不打算先讲 IFFT,心急的读者可以跳到后文中“插值”那一部分。但不建议这么做。
由于递归时动态开 complex 数组巨大的常数,有些题是会 TLE 的(虽然模板题过了),我们需要学习非递归版的。
我们来看一下我们的递归过程:
step 1: | 0 1 2 3 4 5 6 7 |
step 2: | 0 2 4 6 | 1 3 5 7 |
step 3: | 0 4 | 2 6 | 1 5 | 3 7 |
step 4: | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
其中 step 是我们递归的层数。
我们观察一下第一层和第四层:
0 1 2 3 4 5 6 7
0 4 2 6 1 5 3 7
我们写出其二进制:
000 001 010 011 100 101 110 111
000 100 010 110 001 101 011 111
发现什么没有?我们发现第一层的二进制反过来就变成了第四层的二进制。
所以我们可以根据第一层的二进制,来预处理出来第四层的二进制。
void init(int len)
{
int b=log2(len);
for(int i=1;i<len;i++)rev[i]=(rev[i>>1]>>1)+((i&1)<<(b-1));
}
/*
这个 rev 就是 i 的二进制倒过来后的二进制的数
为什么可以这样递推呢?
我们考虑 2*i=(i<<1)
那么反过来的二进制 rev[2*i]=(rev[i]>>1)
所以可以写成 rev[i]=(rev[i>>1]>>1),这里 i 为偶数
考虑到 2*i+1=(i<<1)+1
反过来的二进制是 rev[2*i+1]=(rev[i]>>1)+1
所以可以写成 rev[i]=(rev[i>>1]>>1)+(1<<(b-1)),这里 i 为奇数,其中 b 是 log2(len)
把它们合起来,就变成了最终形式:rev[i]=(rev[i>>1]>>1)+((i&1)<<(b-1))
*/
然后根据递归的合并过程,我们用迭代模拟递归,即枚举长度 1,2,4,然后两两合并。具体的看代码。
void FFT(complex<lf>*a,int n)
{
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]); // 按照刚刚的把 a 的顺序调整到最后一层
for(int len=1;len<=(n>>1);len<<=1) // 枚举合并后的长度的一半
{
complex<lf>wn={cos(PI/len),sin(PI/len)}; // 单位根。注意此时由于枚举的长度是一半,所以 PI 不需要 *2
for(int i=0;i<n;i+=(len<<1)) // 枚举合并的每一个区间的起始位置
{
complex<lf>w={1,0};
for(int j=0;j<len;j++,w*=wn) // 枚举区间的每一个元素
{
complex<lf>a0=a[i+j],a1=w*a[i+j+len]; // 好像这里叫做蝴蝶操作,不过这不重要,没什么用
a[i+j]=a0+a1,a[i+j+len]=a0-a1; // 正常计算即可
}
}
}
}
这样非递归版的居然比递归版的快了近 1 倍。
插值
其实完整的 FFT 并没有做完。
我们刚刚只是把系数表达式转化成了值表达式。
现在把其对应位置相乘得到了答案。
但是答案依然是值表达式,我们还需要转化成系数表达式,我们称这一步为插值。
一般把这一步叫做 IFFT(Inverse Fast Fourier Transform,快速傅里叶逆变换)。
做法的解释有很多,我用矩阵来解释一下。
用矩阵的角度看待 FFT
想一想求值的时候我们是在干什么,是不是找一堆 x 然后代入求 f(x)?
就是这些式子:
f(x_0)=p_0+p_1x_0+p_2x_0^2+\cdots+p_{n-1}x_0^{n-1}\\
f(x_1)=p_0+p_1x_1+p_2x_1^2+\cdots+p_{n-1}x_1^{n-1}\\
f(x_2)=p_0+p_1x_2+p_2x_2^2+\cdots+p_{n-1}x_2^{n-1}\\
\vdots\\
f(x_{n-1})=p_0+p_1x_{n-1}+p_2x_{n-1}^2+\cdots+p_{n-1}x_{n-1}^{n-1}
\end{array}
实际上可以写成矩阵的形式:
f(x_0) \\
f(x_1) \\
f(x_2) \\
\vdots \\
f(x_{n-1})
\end{bmatrix}=
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{bmatrix}
\begin{bmatrix}
p_0 \\
p_1 \\
p_2 \\
\vdots \\
p_{n-1}
\end{bmatrix}
我们知道此时 x_k=\omega^k,可以改写成如下形式:
f(\omega^0) \\
f(\omega^1) \\
f(\omega^2) \\
\vdots \\
f(\omega^{n-1})
\end{bmatrix}=
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \omega & \omega^2 & \cdots & \omega^{n-1} \\
1 & \omega^2 & \omega^4 & \cdots & \omega^{2(n-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)}
\end{bmatrix}
\begin{bmatrix}
p_0 \\
p_1 \\
p_2 \\
\vdots \\
p_{n-1}
\end{bmatrix}
事实上那个 n\times n 的矩阵被称为离散傅里叶变换(DFT)矩阵,不过这不重要。
用矩阵的角度看待 IFFT
事实上本质上我们要根据很多 (x,f(x)) 的二元组解出所有 p_k。
这不就直接把 DFT 求个逆就好了吗:
p_0 \\
p_1 \\
p_2 \\
\vdots \\
p_{n-1}
\end{bmatrix}=
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \omega & \omega^2 & \cdots & \omega^{n-1} \\
1 & \omega^2 & \omega^4 & \cdots & \omega^{2(n-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)}
\end{bmatrix}^{-1}
\begin{bmatrix}
f(\omega^0) \\
f(\omega^1) \\
f(\omega^2) \\
\vdots \\
f(\omega^{n-1})
\end{bmatrix}
这个逆矩阵我让 DeepSeek 帮我们求了,所以改写成如下:
p_0 \\
p_1 \\
p_2 \\
\vdots \\
p_{n-1}
\end{bmatrix}=\dfrac{1}{n}
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \omega^{-1} & \omega^{-2} & \cdots & \omega^{-(n-1)} \\
1 & \omega^{-2} & \omega^{-4} & \cdots & \omega^{-2(n-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \omega^{-(n-1)} & \omega^{-2(n-1)} & \cdots & \omega^{-(n-1)(n-1)}
\end{bmatrix}\begin{bmatrix}
f(\omega^0) \\
f(\omega^1) \\
f(\omega^2) \\
\vdots \\
f(\omega^{n-1})
\end{bmatrix}
诶这是不是跟之前的 DFT 超级像?
IFFT 代码
所以可以直接把之前的 FFT 拿过来,然后改一行代码,再加一行代码即可:
void IFFT(complex<lf>*a,int n)
{
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=1;len<=(n>>1);len<<=1)
{
complex<lf>wn={cos(PI/len),-sin(PI/len)}; // 这里改成虚部 - 的
for(int i=0;i<n;i+=(len<<1))
{
complex<lf>w={1,0};
for(int j=0;j<len;j++,w*=wn)
{
complex<lf>a0=a[i+j],a1=w*a[i+j+len];
a[i+j]=a0+a1,a[i+j+len]=a0-a1;
}
}
}
for(int i=0;i<n;i++)a[i]={a[i].real()/n+0.5,a[i].imag()}; // 再加上这一行,矩阵最前方的 1/n
}
定义单位根时加负号是因为 \omega^{-1}=e^{\frac{-2\pi i}{n}}=\cos(\frac{2\pi}n)-i\sin(\frac{2\pi}n)。
有没有注意到 +0.5 这个操作?那是因为复数的精度误差太大了!
这代码这么像,两个东西显然可以合并啊:
int rev[N];
void init(int len)
{
int b=log2(len);
for(int i=1;i<len;i++)rev[i]=(rev[i>>1]>>1)+((i&1)<<(b-1));
}
void FFT(complex<lf>*a,int n,int type=1)
{
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=1;len<=(n>>1);len<<=1)
{
complex<lf>wn={cos(PI/len),type*sin(PI/len)};
for(int i=0;i<n;i+=(len<<1))
{
complex<lf>w={1,0};
for(int j=0;j<len;j++,w*=wn)
{
complex<lf>a0=a[i+j],a1=w*a[i+j+len];
a[i+j]=a0+a1,a[i+j+len]=a0-a1;
}
}
}
}
void IFFT(complex<lf>*a,int n){FFT(a,n,-1);for(int i=0;i<n;i++)a[i]={a[i].real()/n+0.5,a[i].imag()};}
这就是全部的 FFT 了。
03. 总结
- 我们用多项式乘法提出了 FFT。
- 我们思考把多项式用对应点的值表示。
- 多项式的值需要选取合适的点。
- 我们首先想到了利用相反数。
- 但是这样不方便递归,所以我们想到了复数。
- 我们使用 1 的 n 个 n 次方根,这样平方完,依然是正负成对出现的。
- 这也是 FFT 的精髓。
- 当我们反过来做插值的时候,我们发现 IFFT 居然可以用 FFT 来解决。
- 这样就做完了所有的问题。
- 不得不感叹 FFT 真的太精巧了。
04. 模板题代码
模板题在这里。
#include<bits/stdc++.h>
#define Code using
#define by namespace
#define wjb std
Code by wjb;
int in()
{
int k=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9')k=k*10+c-'0',c=getchar();
return k*f;
}
void out(int x)
{
if(x<0)putchar('-'),x=-x;
if(x<10)putchar(x+'0');
else out(x/10),putchar(x%10+'0');
}
typedef double lf;
const lf PI=acos(-1);
const int N=(1<<21)+20;
int rev[N];
void init(int len)
{
int b=log2(len);
for(int i=1;i<len;i++)rev[i]=(rev[i>>1]>>1)+((i&1)<<(b-1));
}
void FFT(complex<lf>*a,int n,int type=1)
{
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=1;len<=(n>>1);len<<=1)
{
complex<lf>wn={cos(PI/len),type*sin(PI/len)};
for(int i=0;i<n;i+=(len<<1))
{
complex<lf>w={1,0};
for(int j=0;j<len;j++,w*=wn)
{
complex<lf>a0=a[i+j],a1=w*a[i+j+len];
a[i+j]=a0+a1,a[i+j+len]=a0-a1;
}
}
}
}
void IFFT(complex<lf>*a,int n){FFT(a,n,-1);for(int i=0;i<n;i++)a[i]={a[i].real()/n+0.5,a[i].imag()};}
complex<lf>a[N],b[N];
int main()
{
int n=in(),m=in();
for(int i=0;i<=n;i++)a[i]={in(),0};
for(int i=0;i<=m;i++)b[i]={in(),0};
int len=1;while(len<=n+m)len<<=1;
init(len);
FFT(a,len),FFT(b,len);
for(int i=0;i<len;i++)a[i]*=b[i];
IFFT(a,len);
for(int i=0;i<=n+m;i++)out(a[i].real()),putchar(' ');
return 0;
}
尾言
\sout{\LaTeX} 太难打啦啊啊!
在代码的海洋里,我们都是追逐算法星光的旅人。快速傅里叶变换在时光里生长,每一轮迭代都凝结着前人智慧的结晶。或许此刻你正为迭代实现的位逆序而困惑,为单位根的选择而辗转,但若将视角拉长,这些多项式终将编织成照亮前路的银河。
对所有 OIer 而言,那些调试到凌晨的夜晚,那些反复优化的常数,那些 AC 后颤抖的指尖,都将沉淀为生命里珍贵的底色。无论未来是站在领奖台的聚光灯下,还是转身走向更广阔的天地,请记得:你曾在 OI 的星空中留下过属于自己的轨迹。
愿我们永远保持对未知的好奇,像 FFT 处理多项式般优雅地接纳所有可能的挑战。无论未来走向何方,这段为 OI 燃烧的岁月,都将是我们回望时最璀璨的星辰。前路漫漫亦灿灿,愿所有努力终不被辜负,AC 常伴,未来可期。