你看看函数 f 第二个的式子,当 x 与 y 互质且 1 < x \le y 时,函数值是 u,那么这一种情况之和就是 u \times \varphi(y)。第三个式子,当 x 是 y 的因数且 x \not = 1 时,是 -x \times y,所以第二种情况之和就是 y 的因子和与 y 的乘积的相反数,即 - \displaystyle \sum_{x \mid y} x \times y。你可能会好奇为什么有第一个式子,因为当 x = 1 时,第二三个式子(不要前面的那一个不等式)都是成立的,所以这个玩意的函数值就是 u \times 1 - 1 \times y = u - y,这也是为什么第二个式子的条件是 1 < x \le y,第三个式子的条件是 x \not = 1 了。
综上所述,我们可以将式子化为:
\displaystyle \sum_{i = l}^{r} u \times \varphi(a_i) - num_{a_i}
其中 num_{a_i} 就是 \displaystyle \sum_{x \mid y} x \times y。告诉 a_i,线性筛可以预处理得到 \varphi 值,然后预处理出 num 数组(因数和的与数的乘积)。
给定 l, u,求最大的 r,使得上面的函数值最大。我们发现可以使用前缀和处理掉 l 到 r 的循环,于是:
u \times (prephi_{r} - prephi_{l - 1}) - (sum_{r} - sum_{l - 1})
我们为了~~方便好看~~,换个名字,将 $prephi$ 看作 $x$,把 $sum$ 看作 $y$,然后再将函数值设为 $b$,就有:
$$
u \times (x_{r} - x_{l - 1}) - (y_{r} - y_{l - 1}) = b
$$
因为 $l$ 给定,所以说 $x_{l - 1}, y_{l - 1}$ 不变,相当于我们的坐标轴平移了一下,所有点该怎么怎么样,相对位置不会发生改变,我们不妨将其写成:
$$
u \times x_{r} - y_{r} = b
$$
学过初二的同学都知道一次函数的一般式:
$$
y = k \cdot x + b
$$
如果你学过斜率优化(不学也没关系)就会更好的理解这里的类比。这不就是一个一次函数吗?移项:
$$
y_{r} = u \times x_{r} - b
$$
我们要求让 $b$ 最大,那么 $-b$ 就应该最小。每一对 $x, y$ 的值就相当于平面直角坐标系上的一个点,我们相当于是已知一次函数斜率及函数值,求截距,但是如果暴力算的话每一次都是 $O(n)$。~~那咋搞啊哥?~~
我们不妨数形结合画个图:
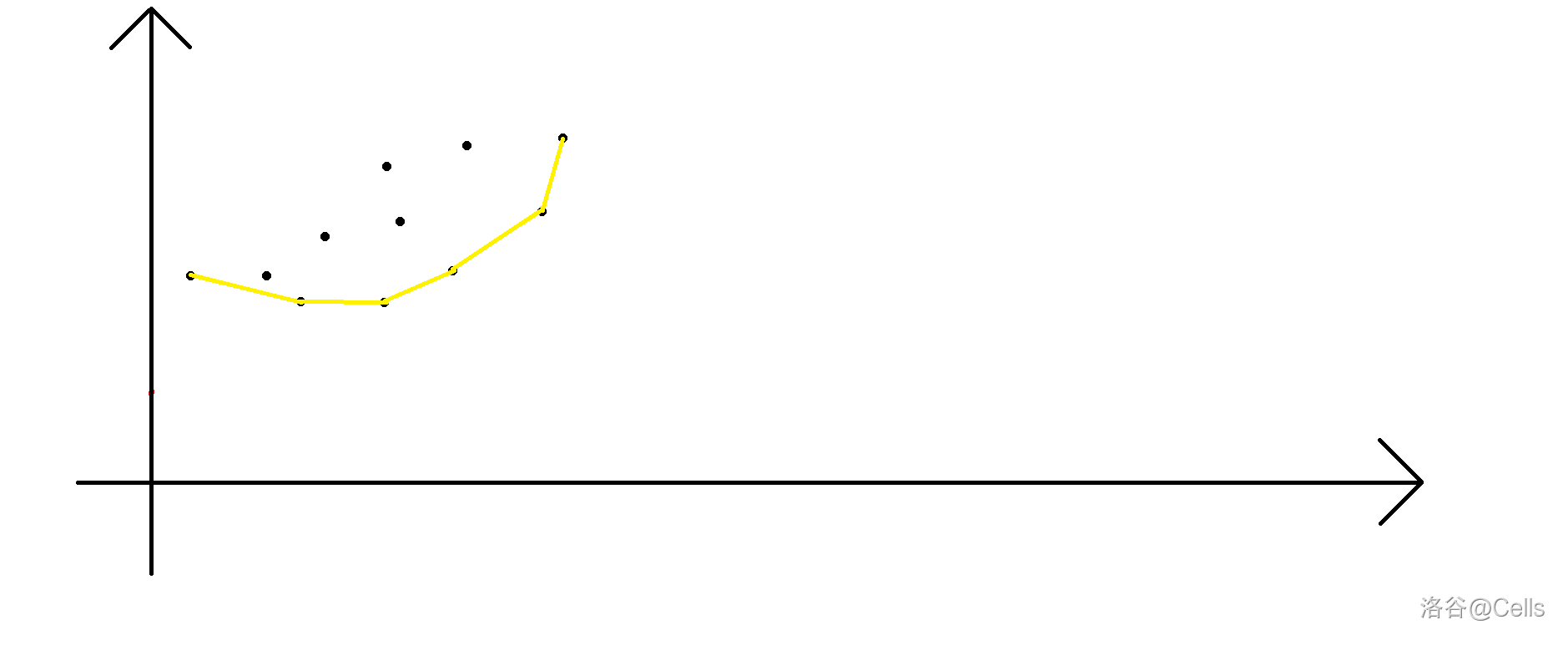
是的,我们发现在凸包内的点无论斜率是多少,都取不到,如果你学过斜率优化 ~~(又来)~~,就更能理解了,如果不会维护凸包就上谷找板子吧,简单来说就是单调栈维护点与点之间的斜率。
另外在这道题中因为斜率始终是正数,所以只需要维护下凸包。但是这样的时间复杂度仍然不算理想,我们通过模拟发现,这不就当于是斜率为 $u$ 的直线去《切》凸包。

观察斜率 $u$ 和切点左右线段的斜率关系。
诶?左边线段的斜率小于 $u$,右边线段的斜率大于 $u$,又因为我们的凸包斜率始终有单调性,所以可以二分 $\log$ 时间查找。
注意 $a_i \le 10^6$,$num$ 数组可能会爆 `long long`,需要开 `__int128`,同理前缀和 $x, y$ 数组也会爆。并且由于只给定 $l$,要求区间的右端点 $r$,所以 $l \le r$,但是因为全局的凸包和 $l$ 右边的凸包可能长相不一样(绿色和黄色):

所以我们需要从后往前遍历边加点,边处理询问,所以需要离线询问并排序。
## Code
```c++
# include <bits/stdc++.h>
# define int long long
# define fir first
# define sec second
# define vec vector
# define pb push_back
# define mem(a, b) memset(a, b, sizeof(a))
# define rep(i, a, b) for(int i = (a); i <= (b); ++ i)
# define pre(i, a, b) for(int i = (a); i >= (b); -- i)
using namespace std;
using LL = long long;
using PII = pair<int, int>;
const int N = 5e5 + 10, A = 1e6 + 10;
int n, m, top, tot;
int a[N], stk[N], phi[A], prime[N];
__int128 x[N], y[N], num[A];
vec<PII> q[N];
PII answer[N];
int calc(int u, int l, int r){
return u * (x[r] - x[l - 1]) - (y[r] - y[l - 1]);
}
void sieve(int n){
rep(i, 1, n){
for(int j = i; j <= n; j += i){//预处理因子和
num[j] += i;
}
}
phi[1] = 1;//线性筛的时候处理phi
rep(i, 2, n){
if(!phi[i]) prime[++ tot] = i, phi[i] = i - 1;
for(int j = 1; prime[j] * i <= n; j ++){
if(i % prime[j] == 0){
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
sieve(A - 10);
cin >> n >> m;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n){//处理phi和因子和与数乘积的前缀和
x[i] = phi[a[i]] + x[i - 1];
y[i] = a[i] * num[a[i]] + y[i - 1];
}
rep(i, 1, m){
int u, l;
cin >> u >> l;
q[l].pb({u, i});//离线询问桶排
}
pre(i, n, 1){//从后往前
while(top > 1 && (y[stk[top]] - y[stk[top - 1]]) * (x[i] - x[stk[top - 1]]) < (y[i] - y[stk[top - 1]]) * (x[stk[top]] - x[stk[top - 1]])) top --;//维护下凸包
stk[++ top] = i;//这里的i和离线是的l都是a数组的编号,所以是相同的含义
rep(j, 0, (int)q[i].size() - 1){
int u = q[i][j].fir, id = q[i][j].sec;
int l = 1, r = top - 1, res = top;//因为l = top - 1,所以说top需要单独计算
while(l <= r){
int mid = l + r >> 1;
if((y[stk[mid]] - y[stk[mid + 1]]) < u * (x[stk[mid]] - x[stk[mid + 1]])) r = mid - 1, res = mid;//建议手模这个过程,注意栈中的编号是反着的
else l = mid + 1;
}
int ans = calc(u, i, stk[res]), pos = stk[res];
answer[id] = {ans, pos};
}
}
rep(i, 1, m) cout << answer[i].fir << " " << answer[i].sec << "\n";
return 0;
}
```
写这篇题解一是教练压力的,另一个确实这题很好,我自己的计算几何里面凸包等玩意也没学好,写一下也能加深印象,这篇题解就到这里,感谢你的观看 QwQ。