回文自动机小记

· · 算法·理论

1.基本元素与构造

每个节点表示原串的一个回文子串，不同的节点表示的回文子串本质不同。

转移边表示给当前串左右同时加上某个字符。若有 u\rightarrow v ，则称 u 为 v 的前驱， v 为 u 的后继（之一）。

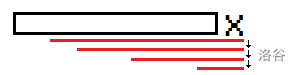
称从结尾在原串末尾的最长回文子串开始向上跳 $fail$ 得到的链为**终止链**，其在原串中对应着这样的一系列回文子串。 ![](https://cdn.luogu.com.cn/upload/image_hosting/upq9smwa.png) 即原串的所有回文后缀。 - ## 回文自动机的经典构造方法 增量法构造，每次在原串末尾加入一个字符，不妨设为 $\rm x$。 考虑加入 $\rm x$ 后的新回文后缀，如下图 : ![](https://cdn.luogu.com.cn/upload/image_hosting/1sb2zdha.png) - **性质①** 每次最多只会加入一个新的本质不同的回文串，且是所有回后缀中最长的。 如图，红色串为最长回文后缀,绿色串为某个较短的回文后缀。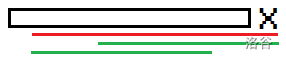 ![](https://cdn.luogu.com.cn/upload/image_hosting/oqr9euk4.png) 则根据回文的性质,绿色串必然在之前已经出现过了。 **推论** ：本质不同的回文子串(回文自动机的点数)不超过 $|S|$。 现在，问题就是如何找到这个最长的新回文后缀。 对于每个新回文后缀，若在其两侧去掉一个 $\rm x$ ，就是一个旧的回文后缀。 考虑新出现的回文串(红色)，则绿色部分（前驱）为旧终止链中的某个串。 ![](https://cdn.luogu.com.cn/upload/image_hosting/3upv8peg.png) 那么，可以暴力跳旧终止链，并检查对应回文串左侧是否恰好有一个 $\rm x$。 由于终止链上长度是由下而上递减的，一旦找到一个符合要求的点 $v$ ，即找到了最长的新回文后缀。 若这个 $v$ 已经有 $\rm x$ 出边，则表示该最长回文后缀已经在前面出现过，找出 $d:v\xrightarrow{\rm x}d$ ，本次终止链末尾即为 $d$。 否则，最长回文后缀是全新的，新建点 $u$ 装这个后缀，连一条 $v\xrightarrow{\rm x}u$ ，且 $u.len=v.len+2$。 还有一个问题是，该串的 $fail$ 指向的新次长回文后缀如何寻找。 可以顺着终止链继续找到旧的回文后缀 $v'$ 满足左边有一个 $\rm x$。 根据 **性质①** 的证明，新次长回文后缀在前面出现过，所以此时 $v'$ 必有 $\xrightarrow{\rm x}$ 出边。 找出 $u':v'\xrightarrow{\rm x}u'$ ,则 $u.fail=u'$。 - **复杂度证明** 每次加入字符时，只会新增一个点和一个转移，状态总量显然是 $O(n)$ 的。 每次暴力跳终止链的复杂度令人怀疑，其实也是 $O(n)$ 的。 设当前终止链长度为 $k$ ，若跳过 $d$ 步才找到 $u.fail$ ，则新的由 $u$ 开始的终止链长度为 $k-d+1$。 终止链长度的消长相当于蜗牛爬杆，复杂度是正确的均摊 $O(n)$ 。 - **实现细节** 奇回文串的构造并不完全遵守“左右同时加上某个字符”的规则，中心字符是单独出现的。 所以，需要建立奇偶两个根，规定奇根转移得出的都是奇回文串，偶根转移得出的都是偶回文串。 对奇根采取特殊规则，走转移只会增加一个字符，即为某个奇回文串的重心字符。 为了兼容，可以把奇根的 $len$ 置为 $-1$ （这样可以看作加入两个重叠的字符）。 偶根的 $fail$ 为奇根 (奇根的限制比偶根少，若没有偶回文串，尝试一下奇回文串的最低要求 ： 单个字符) ，奇根的 $fail$ 指向自己。 加入字符 $\rm x$ 的构造过程中，如果发现串没有新次短回文后缀，则意味着前面的串中根本没有字符 $\rm x$，此时将最长回文后缀（只有一个字符 $\rm x$） 的 $fail$ 置为偶根。 可能父亲和出边到自己的点是同一个点，要注意赋值顺序问题。 此外，为了避免越界，让字符串从 $1$ 开始标号，并把第 $0$ 个字符标记为 $-1$。 ```cpp struct Node {int t[26],f,len;}a[MaxN]; int tn,las; char str[MaxN]; void ins(int k,int c) { int p=las; //las是旧终止链的末端 while(str[k-a[p].len-1]!=c)p=a[p].f; //找到新最长回文后缀的前驱 if (!a[p].t[c]){ //若新最长回文后缀是全新的 int np=las=++tn,v; //新建点 np 装新最长回文后缀，其为新终止链的末端 for(v=a[p].f;str[k-a[v].len-1]!=c;v=a[v].f);//找到新次长回文后缀的前驱 if (!a[v].t[c])a[np].f=2; //找不到,则 fail 为偶根 (空回文串) else a[np].f=a[v].t[c]; //否则由前驱找到新次长回文后缀 a[a[p].t[c]=np].len=a[p].len+2; }else las=a[p].t[c]; //若新最长回文后缀出现过，简单地更改终止链末端 } void Init() {a[1].len=-1;a[1].f=a[2].f=1;tn=las=2;} //奇根为1 偶根为2 ``` - ## 经典应用 - **本质不同回文串数** 点数$-2$ (除去两个根) - **各个回文子串的出现次数** 构造过程中，每加入一个字符时，相当于把整条终止链的出现次数 $+1$ 。 那么我们把每次的终止链末尾权值 $+1$ ，最后在 $fail$ 树上求和即可。 实际操作中，由于编号大的点一定不会是编号小的点的父亲，不需要建立树，直接按照编号求和也可。 - [P3649 [APIO2014]回文串](https://www.luogu.com.cn/problem/P3649) 求出出现次数之后，乘上 $len$ 取 $\max$ 即可。 [评测记录](https://www.luogu.com.cn/record/36494325) - [P5496 【模板】回文自动机（PAM）](https://www.luogu.com.cn/problem/P5496) 本题相当于在线地询问终止链长度，记录 $dep$ 并递推。 [评测记录](https://www.luogu.com.cn/record/36494752) - [P4287 [SHOI2011]双倍回文](https://www.luogu.com.cn/problem/P4287) 注意到双倍回文串也是一个回文串，此题可以转化成对于每个回文串，判定是否能拆成两个相同的偶回文串。 可以从该点跳 $fail$ 找到自己的所有回文后缀。若有长度恰为 $len/2$ 的，则符合要求。 暴力跳复杂度显然不对劲。 建立 $fail$ 树，$dfs$ 时开一个桶记录到根的链中各个点的 $len$ ，对于每个点只需要查看桶中为 $len/2$ 的位置。 [评测记录](https://www.luogu.com.cn/record/36496018) - [P4555 [国家集训队]最长双回文串](https://www.luogu.com.cn/problem/P4555) 对于每个位置，记录在此结束和开始的最长回文串长度，然后拼接即可。 可以正反分别构造一次回文自动机来求出。 [评测记录](https://www.luogu.com.cn/record/36506828) - [CF17E Palisection](https://www.luogu.com.cn/problem/CF17E) 可以转化为求不相交的回文串对子数。 枚举靠前的串的结尾位置 $i$ ，则靠后的串只需要在 $i$ 以后开始即可。 记录 $L[i]$ 为在 $i$ 开始的回文串个数, $R[i]$ 为结束。(即为终止链长度) 可以正反构造两次回文自动机来求出。 $\sum\limits_{i=1}^{|S|}R[i]\sum\limits_{j=i+1}^{|S|}L[j]$ 即为答案。 [评测记录](https://www.luogu.com.cn/record/36542284) - [P5555 秩序魔咒](https://www.luogu.com.cn/problem/P5555) 其实就是双串最长公共回文子串。 对两个串分别建立回文自动机，由于状态量很少，可以选取两个自动机相同的转移进行搜索，即可得到所有的公共回文子串。 [评测记录](https://www.luogu.com.cn/record/36556331) - [P5685 [JSOI2013]快乐的 JYY](https://www.luogu.com.cn/problem/P5685) 题意就是求两个字符串的相等回文子串对子数。 类似上一题，对同样的转移搜索，将对应节点的出现次数相乘求和。 [评测记录](https://www.luogu.com.cn/record/36557597) 另一种做法是，先建立 $A$ 的 $\rm PAM$ ，然后用 $B$ 在上面跑匹配。 逐个加入 $B$ 中的字符，维护在 $A$ 中能匹配到的最长回文后缀。 注意，匹配的时候是双向扩展，除了检查自动机的出边外，还要检查 $B$ 串对应的两个字符是否相等。 若匹配到 $u$ 点，则可以视为包含到了所有 $u$ 的祖先，对次数的贡献就是这一条链的 $siz$ 和。 那么预先向下求和即可。 [评测记录](https://www.luogu.com.cn/record/36557978) - [CF835D Palindromic characteristics](https://www.luogu.com.cn/problem/CF835D) 加强版 原题 $|S|\leq 5000$ ，利用 $\rm PAM$ 可以做到 $|S|\leq 5\times 10^6$。 记 $\rm PAM$ 中串 $u$ 长度不超过 $len/2$ 的**最长**回文后缀为 $u.half$。 在构造回文自动机的同时，若新产生的点为 $np$ ，且找到 $p\xrightarrow{\rm x}np$ ，那么先找到 $p.half$ ，然后向祖先跳直到能产生对应回文后缀为止(注意不能直接检查有无出边,就算有也可能只是前面的)。 此时出边指向的那个点就是 $u.half$。复杂度证明类似前面对终止链长度变化的分析。 记 $f[u]$ 表示回文串 $u$ 的阶数，有如下 $\rm DP$ : $\begin{cases}f[u]=f[u.half]+1&(u.half.len=u.len/2)\\f[u]=1&(u.half.len<u.len/2)\end{cases}

评测记录

能够发现,答案肯定是在某次 2 操作之后暴力加字符得来的。

我们建立原串的回文自动机,然后分别求出每个(偶)回文子串 S 的构造代价 S ,原串的构造代价即为 n+\min F[S]-len[S]。

考虑如何构造一个回文串,不难发现,最优策略的最后一步操作一定是 2。

看看上一次的 1 是怎么用的。

如果用在外面，则可以视为在两侧同时加了一个字符，则可以按照从后缀自动机的转移边来 DP。

转移为 f[v]=\min(f[v],f[u]+1)\ (u\rightarrow v)

如果用在里面，则必然先造好一个后缀，这里只需要考虑回文后缀。

设 S 为目标， T1,T2 为两个能够转移的回文后缀,若 |T1|>|T2| 则 T1 不劣于 T2。

也就是说，只需要考虑该串的 half （长度不超过 len/2 的最长回文后缀）。

证明 : T 构造出半个 S 的代价 : F[T]+|S|/2-len[T]

由于 T2 是 T1 的后缀,可以在 T2 前面加字符得到 T1 ,则有 F[T1]\leq F[T2]+len[T1]-len[T2]

\Rightarrow F[T1]-len[T1]\leq F[T2]-len[T2] [评测记录](https://www.luogu.com.cn/record/36564131) - ## 更多构造方式 - **复杂度非均摊的构造 & 可持久化** 暴力跳终止链是经典构造算法复杂度需要依赖于均摊的重要原因。 回忆一下我们跳终止链是为了找什么，不难发现，在找“祖先中第一个左侧有字符 $\rm x$ 的节点”。 那么，不妨记 $u.tr[c]$ 表示 $u$ 的祖先中第一个左侧有字符 $\rm x$ 的节点。 若 $u$ 是 $v$ 的祖先，则 $v$ 继承 $u.tr$ ，并将自己左侧字符对应的 $tr$ 修改。 这样就不需要暴力跳终止链了，然而由于需要复制数组，复杂度是 $O(n\Sigma)$ 的。 若使用可持久化数组，即可实现快速创建副本，复杂度变为 $O(n\log \Sigma)$ ，也可以支持可持久化。 - **两侧同时插入** 考虑维护 $fail'$ 指针表示自动机中串的最长回文前缀。由回文，不难发现回文前缀同时也是回文后缀，所以总有 $fail'=fail$ ，不必额外维护。 所以，只需要记下正反两条终止链的末端就可以实现两侧插入了。 注意，当整个串变成回文串的时候，要更新另一侧的末端。 具体的讨论和实现请见例题 ： [HDU5421 Victor and String](http://acm.hdu.edu.cn/showproblem.php?pid=5421) | [Sol](https://www.luogu.com.cn/blog/command-block/str-ji-lu-hdu5421-victor-and-string) # 2.回文 $\bf Border$ 理论 需要先在 [Border理论小记](https://www.luogu.com.cn/blog/command-block/border-li-lun-xiao-ji) 学习前置芝士。 - **定理①** 回文串的回文后(前)缀与其 $\rm Bd$ 对应。 **证明** : 设串长为 $n$。长度为 $l$ 的回文后缀 $\Leftrightarrow\rm S[n-i+1]=S[n-l+i]=S[l-i+1] 图解如下，其中 $u,v$ 均为回文串，$v$ 是 $u$ 的后缀。 $\large\begin{aligned} &\qquad\qquad\boxed{\qquad\qquad\qquad v \qquad\qquad\qquad} \\&\boxed{\qquad\qquad\qquad\qquad u \qquad\qquad\qquad\qquad} \\&\boxed{\qquad\qquad\qquad {\normalsize{\large v}_R}\ \ \ \quad\qquad\qquad} \end{aligned}

由于回文的定义 v_R=v ，显然 v 是 u 的 \rm Bd。

推论 ：某个串的回文后(前)缀长度可以拆分为 O(\log n) 个等差数列。

设回文串 s 的长度为 n，循环节为 t，周期为 p=|t|。

将 s 表示成 s=t^{k}t_1 ，其中 t_1 是 t 的严格前缀。令 t=t_1t_2。有图 ：

&\qquad\qquad\qquad\quad\ \ \boxed{\quad{t}_1\quad}\boxed{\quad\ \,t_{2}\,\ \quad} \\&\boxed{\qquad\quad\ t_{}\ \quad\qquad}\boxed{\qquad\quad\ t_{}\ \quad\qquad}\boxed{\quad{t}_1\quad} \\&\boxed{\qquad\qquad\qquad\qquad\,\ \ s\ \ \ \qquad\qquad\qquad\qquad} \\&\qquad\qquad\qquad\qquad\qquad\ \ \ \,\boxed{\qquad\quad t_R \quad\qquad} \end{aligned}

由上图可得 t_R=t_1t_2 ，且显然有 t_R={t_2}_R{t_1}_R ，可得 t_1,t_2 均为回文串。不难发现 t_1,t_2 的长度恰为 s-(s\bmod p),(s\bmod p)。

取出前两次匹配 v_1,v_2 ，假设 v_2 不是后缀。

由 \rm Border 论， 2|v|\geq u\Rightarrow\ v 在 u 的匹配位置成一个等差序列，且公差为 v 的周期。

匹配情况如图 ：

&\boxed{\qquad\qquad\qquad\qquad\,\ \ u\ \ \ \qquad\qquad\qquad\qquad} \\&\boxed{\qquad\qquad v_{1}\quad|\quad\qquad} \\&\qquad\qquad\qquad\ \boxed{\qquad\qquad v_{2}\quad|\quad\qquad} \end{aligned}

根据 定理② ，改写 v 的循环节为两个回文串 p_1,p_2 ，则 v=(p_1p_2)^kp_1。

&\boxed{\qquad\qquad\qquad\qquad\,\ \ u\ \ \ \qquad\qquad\qquad\qquad} \\&\boxed{\quad p_1\quad}\boxed{\ \ p_2\ \ }\boxed{\quad p_1\quad} \\&\qquad\qquad\qquad\ \boxed{\quad p_1\quad}\boxed{\ \ p_2\ \ }\boxed{\quad p_1\quad} \end{aligned}

此时不难发现 v_1∪v_2=(p_1p_2)^{2k}p_1 可以形成比 v 更长的回文前缀，矛盾。