概率期望24题

· · 个人记录

不保证没锅，如果你的答案和我的不一样请评论区探讨。
如果你有更快更好的解法，也请评论区见。
本组题目的考点均来自《程序员的数学2》的1-4章。由于第4章我也看得不是很懂，所以不会考很多东西。

签到题

概率的基本概念，等可能事件的概率。

  1. 现有 4 个红球和 2 个白球，随机摸一个，是红球的概率是多少？（如果在本博客中提到随机，默认i.i.d，即随机均匀独立出现）

离散值的贝叶斯公式（无特殊说明，只有红球白球两种）

结合了条件概率，联合概率和贝叶斯公式，期望值的定义。

  1. 现有 6 个球，随机一个 0\sim 6 的整数作为红球数，随机摸一个发现是红球，红球个数的期望是多少？
  2. 现抛 6 次硬币，正面朝上放一个红球，否则放一个白球，随机摸一个发现是红球，红球个数的期望是多少？
  3. 现有 6 个球，随机一个 0\sim 6 的整数作为红球数，随机摸一个发现是红球，放回重抽抽到白球的概率是多少？
  4. 现有 3 个红球，随机一个 0\sim 3 的整数作为白球数，随机摸一个发现是红球，不放回重抽抽到白球的概率是多少？
  5. 现有 3 个红球，随机一个正整数作为白球个数，其中 i 个白球的概率为 2^{-i}，随机摸一个，发现是红球，问白球个数期望值。（允许用desmos等工具或自行编程，保留近似值。）
  6. 现有 6 个球，随机一个 0\sim 6 的整数作为红球数，随机摸一个发现是红球，接下来摸 8 次球，恰有 5 次是红球的概率是多少？

期望，方差与标准差

然而包括大数定律与最小二乘法。

  1. 随机变量 X 的期望为 10，平方的期望为 120，调用 x 变量 100 次，得到的结果平均数的标准差是多少？

  2. 在 [3,6] 中取一个整数 x，在 [x,6] 中取一个整数 p，在 [1,x] 中取一个整数 q，求 p-q 的方差。

  3. 现有 6 个球，其中 4 个红球和 2 个白球。在 0\sim 4 中随机了一个数 x，

    离散值概率综合

    各种1~3章的内容都可能出现，可能会用到数学或者信息学的知识。可能计算较为复杂。

  4. 连续值概率期望，概率密度函数等

    最终的大Boss

答案与解析

签到题

离散值的贝叶斯公式

如上，将平行世界系统 \Omega 横着分成七个 \dfrac{1}{7} 分别表示 0\sim 6 个红球的情况，纵向黄色表示取到红球的世界 \omega 的集合。黄色面积为 \dfrac{1}{2}，相信不用多说。

对于一个区域，这个区域对于期望的贡献为黄色部分占比乘红球数量。

求其总和，得到期望值为 \dfrac{91}{21}。你或许发现了，这个概率可以 O(1) 计算——平方和除以和。

只要把第二题中一开始七个等宽条换成宽度分别为 \dfrac{1}{64},\dfrac{6}{64},\dfrac{15}{64},\dfrac{20}{64},\dfrac{15}{64},\dfrac{6}{64},\dfrac{1}{64} 的条即可。如果你熟悉组合数，可以发现这也是可以快速计算的题。

借助2中的图，同样考虑A~G区对概率的贡献。显然概率贡献是该条占黄色区域的比乘白球概率。

求得总概率为 \dfrac{35}{126}=\dfrac{5}{18}。

相信你应该可以自己把图画出来。将 \Omega 分成四个等宽的条A,B,C,D表示放入 0,1,2,3 个白球的情况。

取出一个红球不放回后，四个区取到黄球的概率分别是 0/2=0/60,1/3=20/60,2/4=30/60,3/5=36/60

总概率为 \dfrac{20}{57}\times\dfrac{0}{60}+\dfrac{15}{57}\times\dfrac{20}{60}+\dfrac{12}{57}\times\dfrac{30}{60}+\dfrac{10}{57}\times\dfrac{36}{60}=\dfrac{17}{57}

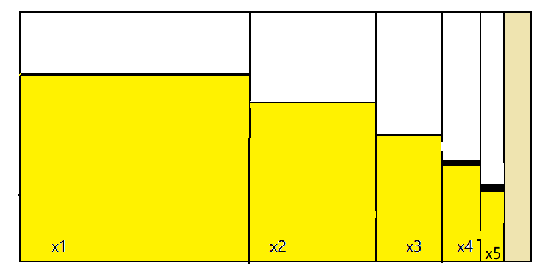
  1. ![image.png](https://i.loli.net/2020/06/13/neCKLiNRb7aHXlS.png)

先将平行世界系统 \Omega 切成无数条，第 i 条宽度为 2^{-i}，然后将每条中取出红球的部分涂成黄色。

通过desmos的计算得到黄色总面积为

S=\sum_{n=1}^{1000000}\dfrac{3}{n+3}\cdot 2^{-n}=0.635532333439

（本来应该用 \inf ，但是desmos不支持）
接下来考虑期望值，也就是每一块黄色乘以对应的权值的结果。

E=\frac{1}{S}\sum_{n=1}^{1000000}\frac{3}{n+3}\cdot n\cdot2^{-n}=1.72045219756

期望，方差和标准差

根据大数定律， $100$ 次的方差为 $1$ 次的 $\dfrac{1}{100}$，所以答案为 $\sqrt{\dfrac{20}{100}}=\dfrac{\sqrt{5}}{5}$。 9. $\dfrac{9}{4}$。 考虑各项独立时，和的方差等于方差的和，意味着 $V[p-q]=V[p-x]+V[x-q]$。 预先计算出 $n=0,1,\ldots,5$ 时 $[0,n]$ 随机抽取一个的方差：分别是 $0,0.25,2/3,1.25,2,35/12$。 因此 $V[p-x]=\dfrac{1}{4^2}(1.25+2/3+0.25+0)=13/24 V[x-q]=\dfrac{1}{4^2}(2/3+1.25+2+35/12)=41/24 V[p-q]=54/24=9/4