子树 题解
b6e0_
·
·
题解
官方题解。
本文中所有未经说明的函数都与题目中形式化题面的定义相同。设 S(x,y) 表示 x 到 y 的简单路径上所有节点的点权和(x 和 y 也算在内),P(x,y) 表示 x 到 y 的简单路径上所有节点的点权积(x 和 y 也算在内),siz_u 表示以 u 为根的子树节点个数,根是哪个节点见语境。
先考虑对于确定的 r,确定的 u,怎么计算 W(u)=\sum_{v=1}^nf(v,u)。
$$\begin{aligned}f(F(x),u)+a_x&=f(F(F(x)),u)+a_{F(x)}\\&=f(F(F(F(x))),u)+a_{F(F(x))}+a_{F(x)}+a_x\\&\cdots\\&=S(x,u)+f(F(u),u)\end{aligned}$$
于是,处理出 $SS_u$ 表示 $\sum_{v\in A_u}S(v,u)$,以 $u$ 为根的子树中节点的 $f$ 和就是 $SS_u+siz_u\cdot f(F(u),u)$。这里给出 $SS$ 的递推式:$SS_u=siz_ua_u+\sum_{v\in B_u,v\ne F(u)}SS_v$。
对于 $x\not\in A_u$ 的情况,以 $F(u)$ 为根,$D(x,u)$ 为节点 $x$ 的深度,拎起一棵树,直接求即可。
当 $u$ 变化时,以 $u$ 为根的子树中节点的 $f$ 和仍然可以用 $SS_u+siz_u\cdot f(F(u),u)$:首先要对于所有节点 $u$ 求出 $SS_u$ 和 $siz_u$,然后对于 $f(F(u),u)$ 的计算,考虑在下图中,将 $u$ 换成它的一个孩子 $v$,$f(F(u),u)$ 会发生什么变化:
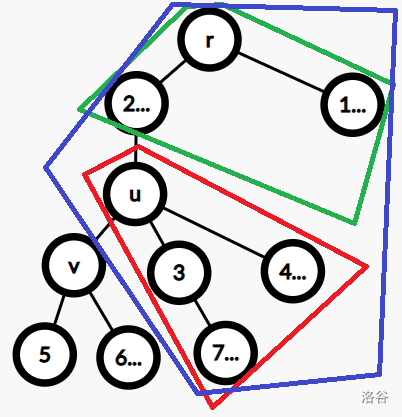
观察图,原来子树外的部分是绿框,现在是蓝框,发现多的部分就是 $u$ 除 $v$ 以外其他孩子的子树和 $u$,也就是图中红色框的部分,按照原来层次传上来的贡献。于是,对于每个节点 $x$,求出 $SP_x=a_x\cdot\max_{y\in B_x,y\ne F(x)}SP_y$,在每次准备将 $u$ 换成 $v$ 时,对于 $u$ 的所有孩子的 $SP$ 按照 dfs 顺序求一个前缀 $\max$ 和后缀 $\max$,转移即可。
到现在,以一次 $\mathcal O(n)$ 的复杂度,求出了 $C(r)$,总时间复杂度是 $\mathcal O(n^2)$,还不够优秀,考虑继续优化。因为这里是对每个节点求一个值,根据套路,考虑换根,即考虑根从 $r_1$ 变到 $r_2$ 时答案的变化。
此处先考虑 $x\not\in A_u$。注意到根 $r$ 的变化,除了 $u=r_1$ 和 $u=r_2$,影响不到你拎起来的这棵树。这棵拎起来的树只跟 $F(u)$,$D(x,u)$ 有关,而这些东西,除了 $u=r_1$ 和 $u=r_2$,在换根时没有变化。类似地,$x\in A_u$ 的情况,只跟子树中有哪些节点有关,除了 $u=r_1$ 和 $u=r_2$,其他的子树都没有变化!于是,用上面的计算方法,只需要特殊处理 $u=r_1$ 和 $u=r_2$ 时的 $W(u)$。~~我太懒了就没有画图。~~
处理 $u=r_1$ 和 $u=r_2$ 时的 $W(u)$ 需要算出一些额外的值:$AS_x$ 表示树中所有节点到 $x$ 路径上的点权和,即 $AS_x=\sum_{y=1}^nS(x,y)$,这个值可以用换根 dp 求出;其他的值可以用类似上面的方法求出。总时间复杂度 $\mathcal O(n)$。代码(建议复制到 IDE 里看):
```cpp
#include<bits/stdc++.h>
using namepace std;
const int mod=998244353;
vector<int>g[500010];
int n,siz[500010];
long long a[500010],ss[500010],as[500010],sp[500010],ssp[500010],uans[500010],ans[500010];//ssp为子树内sp的和,uans[x]表示当r=1时的W(r)
inline int read()//快读
{
char c=getchar();
int x=0;
while(c<'0'||c>'9')
c=getchar();
while(c>='0'&&c<='9'){
x=(x<<3)+(x<<1)+c-'0'; c=getchar();
}
return x;
}
inline void write(int x)//快写
{
if(!x){
putchar('0'); putchar('\n');
return;
}
while(x<0) x+=mod;
int sta[10],tp=0;
while(x){
sta[++tp]=x%10; x/=10;
}
while(tp)
putchar(sta[tp--]+'0');
putchar('\n');
}
void dfs(int x,int f)//求出siz,ss,sp,ssp
{
siz[x]=1;
sp[x]=-1;
for(int i=0;i<g[x].size();i++)
if(g[x][i]!=f)
{
dfs(g[x][i],x);
siz[x]+=siz[g[x][i]];
ss[x]=(ss[x]+ss[g[x][i]])%mod;
sp[x]=max(sp[x],sp[g[x][i]]);
}
ss[x]=(ss[x]+siz[x]*a[x]%mod)%mod;
if(sp[x]==-1)
ssp[x]=sp[x]=a[x];
else
ssp[x]=sp[x]=sp[x]*a[x]%mod;
for(int i=0;i<g[x].size();i++)
if(g[x][i]!=f)
ssp[x]=(ssp[x]+ssp[g[x][i]])%mod;
}
void dp1(int x,int f,long long nf,long long ns)//求出uans,ans[1],as
{
uans[x]=(ss[x]+nf*siz[x]%mod+ns)%mod;
ans[1]=(ans[1]+uans[x])%mod;
if(x!=1)
as[x]=(as[f]-a[f]*siz[x]+a[x]*(n-siz[x])%mod)%mod;
int i,pt=0,lt=g[x].size()-2;
vector<long long>pm,lm;//前缀,后缀最大值
if(x==1)
lt++;
pm.push_back(0);
lm.push_back(0);
for(i=0;i<g[x].size();i++)
if(g[x][i]!=f)
pm.push_back(max(pm.back(),sp[g[x][i]]));
for(i=g[x].size()-1;~i;i--)
if(g[x][i]!=f)
lm.push_back(max(lm.back(),sp[g[x][i]]));
for(i=0;i<g[x].size();i++)
if(g[x][i]!=f)
{
dp1(g[x][i],x,max(max(nf,1ll),max(pm[pt],lm[lt]))*a[x]%mod,(ns+ssp[x]-ssp[g[x][i]]-sp[x]+max(max(nf,1ll),max(pm[pt],lm[lt]))*a[x]%mod)%mod);
pt++;
lt--;
}
}
void dp2(int x,int f)//求出ans
{
ans[x]=(ans[f]-as[f]-uans[x]+as[x]+ssp[x]+sp[x]*(n-siz[x])%mod+as[f]-ss[x]-a[f]*siz[x]%mod)%mod;
for(int i=0;i<g[x].size();i++)
if(g[x][i]!=f)
dp2(g[x][i],x);
}
int main()
{
int i,x,y;
n=read();
for(i=1;i<=n;i++)
a[i]=read()%mod;//进来要先%!否则在比较大小时会出问题
for(i=1;i<n;i++)
{
x=read();
y=read();
g[x].push_back(y);
g[y].push_back(x);
}
dfs(1,0);
as[1]=ss[1];
dp1(1,0,0,0);
for(i=0;i<g[1].size();i++)//不想让节点1再转移一遍,所以直接对1的孩子做
dp2(g[1][i],1);
for(i=1;i<=n;i++)
write(ans[i]);
return 0;
}
```